Contribute to balance, wire in accordance - Emergence of backpropagation from a simple, bio-plausible neuroplasticity rule

year: 2024/05
paper: https://arxiv.org/pdf/2405.14139
website:
code:
connections: biologically inspired, synapses, self-organization, backpropagation, retrograde reward

---

Motivation

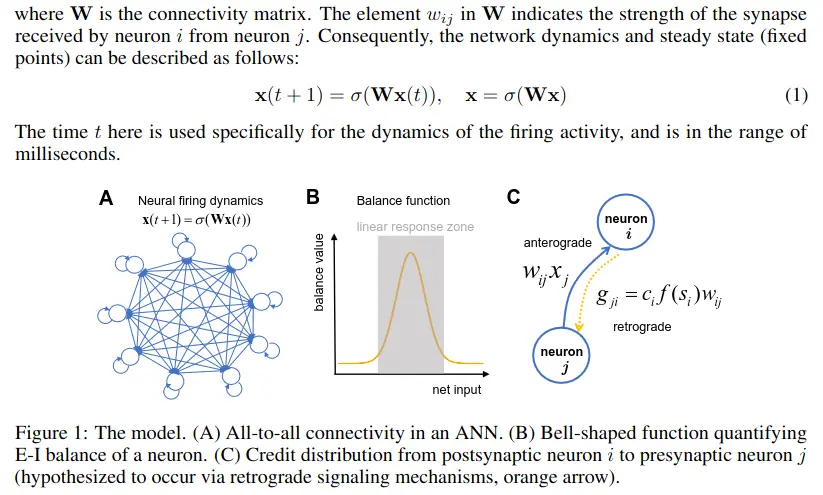
The core conceptual foundation of our neuroplasticity framework is the maintenance of excitation-inhibition (E-I) balance of neurons. E-I balance refers to the equilibrium between excitatory and inhibitory inputs to neurons. Maintaining this balance has been shown to help direct neuronal firing toward the linear response zone, which is essential for efficient information processing and representation.

High-level behaviour

This credit redistribution rule encapsulates three underlying relationships: (i) postsynaptic neurons with more credits give more credits to their presynaptic neurons; (ii) postsynaptic neurons that are more balanced give more credits to their presynaptic neurons; and (iii) presynaptic neurons receive more credits if the synaptic strength is stronger

---

The three factors in this learning rule encapsulate the following relationships: (a) If the postsynaptic neuron has more credits, the synapse will be strengthened more; (b) If the postsynaptic neuron is more balanced, the synapse will be strengthened more. (c) If the presynaptic neuron has a higher firing rate, the synapse will be strengthened more. Separately, the timing for weight updates in equation 4 is expected to operate in the range of seconds to minutes, on stable values of both firing rates $x_j$ as well as of credit values $c_i$.

---

In summary, our new framework operates following three update rules: (1) Neural firing dynamics at the fastest timescale: $\mathbf{x}(t+1)=\sigma (\mathbf{Wx}(t))$; (2) Credit redistribution dynamics at the intermediate timescale: $\mathbf{c}(t+1)=J\mathbf{c}(t)$; (3) Neural plasticity dynamics at the slowest timescale: $\mathbf{W}(t+1)=(c\odot f(s)){\mathbf{x}}^T+\mathbf{W}(t)$

Methodology

We utilize an all-to-all connected neural network to establish our model (Figure 1A), which provides a high degree of generality. The firing activities of neurons are represented as an $n$-dimensional vector $\mathbf{x}(t)$, where the $i$th element $x_i(t)$ reflects the firing activity of the $i$th neuron at time step $t$. The firing activity depends on the nonlinear activation function $\sigma$ and the inputs to each neuron $s(t)=\mathbf{Wx}(t)$,
where $\mathbf{W}$ is the connectivity matrix. The element $w_{ij}$ in $\mathbf{W}$ indicates the strength of the synapse received by neuron $i$ from neuron $j$. Consequently, the network dynamics and steady state (fixed points) can be described as follows:

$$\mathbf{x}(t+1)=\sigma (\mathbf{Wx}(t)),\mathbf{x}=\sigma (\mathbf{Wx})(1)$$

The time $t$ here is used specifically for the dynamics of the firing activity, and is in the range of milliseconds.

! Model reduces exactly to backpropagation in layered neural network … under the sole assumption that the functional metric quantifying the E-I balance of a neuron be chosen to have the functional form of the derivative of its activation function.

Biological plausibility section:

Transclude of neural-oscilation#^a74b58

Interpretation

In the framework of this model, BP can be interpreted as a simple consequence of individual neurons striving to maintain E-I balance. Our simulations demonstrate that this synaptic plasticity rule, when paired with structural plasticity mechanisms like pruning, can lead to the self-organization of different network structures in a fully connected network.

Summary

Our model makes three practical predictions that are experimentally testable. First, the amplitude of retrograde signaling should be highest for balanced neurons, but low for neurons with saturated firing rates or those close to being silent. This is based on the equation $g_{ji}=c_{i}f(s_i)w_{ij}$, where the balance value $f$ approaches zero as a neuron becomes more unbalanced. Second, the ratio of the amplitude of synaptic change to the amplitude of retrograde signal should be proportional to the firing rate of the presynaptic neuron and inversely proportional to synaptic strength. This prediction is derived from the ratio of the credit redistribution rule to the neuroplasticity rule, leading to $\frac{\Delta w_{ij}}{g_{ji}}=\frac{x_i}{w_{ij}}$. Third, during early stages of neural development, associated with a greater degree of plasticity and therefore higher learning rate, the brain is more likely to form across-module connectivity. By contrast, in later stages, associated with lower learning rates, within-module connectivity is more likely.

Limitations

The model we have proposed here possesses a potential limitation. It is the assumption that credit redistribution will converge for the network updating rule to function. Our current mathematical framework does not guarantee the existence of a non-trivial fixed point in the dynamical system for credit redistribution. The matrix $\mathbf{J}$ in Equation 5 does not necessarily have an eigenvalue of one, meaning it could result in convergence to a zero vector or divergence to infinity. We currently circumvent this issue through the plausible means of clamping the credit values of some neurons (technically, even if just one neuron) to a constant. With such clamping, multiple ($\ge 1$) rows of the matrix $\mathbf{J}$ will be replaced by an identity matrix, ensuring the existence of an eigenvalue of one. Consequently, an intriguing observation is that the network’s stability may depend on external credit signals and that spontaneous credit dynamics could lead to instability. Long-term sensory deprivation, which causes cognitive instability and affects connectivity and E-I balance in cortical circuits, is one biological phenomenon that supports this observation. More generally, then, the stability of this model will benefit from further exploration and systematic analysis.

$\text{textexclamdown}$ → External credit signals are introduced in soup.

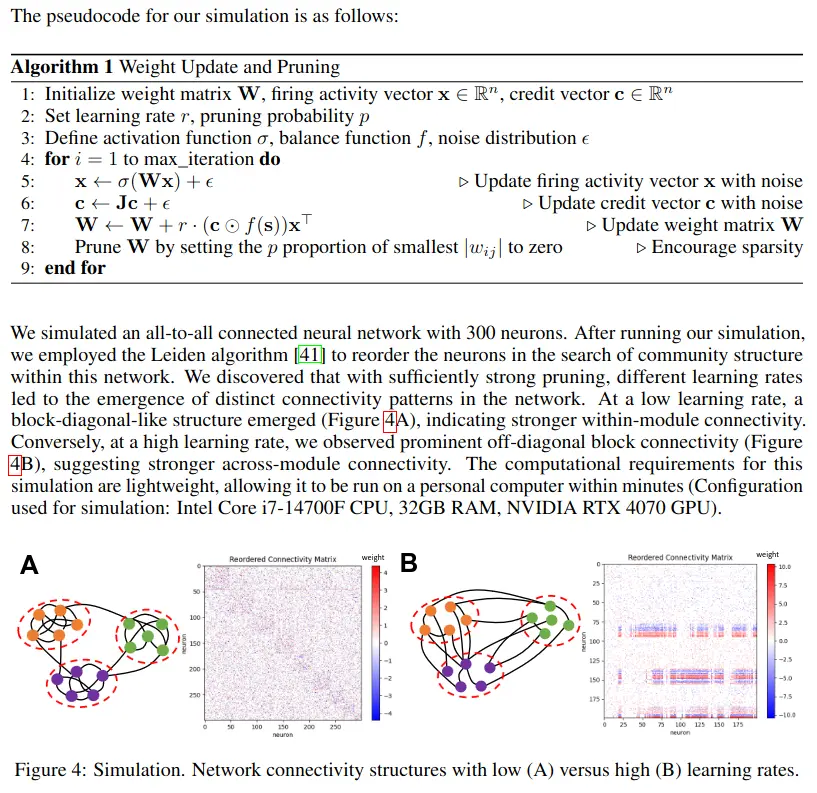
4 Simulation results: Learning rates dictate connectome patterns

We note four key points about the set up of our simulation algorithm. First, for the purposes of this exploration, the simulation algorithm makes one simplifying assumption In the model dynamics, the input/output clamping signal is replaced with a random Gaussian noise term, ϵ. This substitution serves the dual purposes of eliminating the need for specific input-loss pairs from open task datasets, and preventing the system from being trapped indefinitely in a trivial state. Second, to ensure the existence of a non-trivial equilibrium states, the first 10% of the rows of the matrix J were fixed to be a diagonal matrix. This can be interpreted as output clamping for that initial 10% of neurons, thereby guaranteeing the existence of a non-trivial equilibrium state via clamping. Third, in the wiring of biological networks, pruning of weak synaptic connections, a mechanism of structural plasticity, co-occurs with classical mechanisms of synaptic plasticity. Therefore, for the purposes of our exploration of neural connectivity structures, we pair our new synaptic plasticity rule with pruning. This encourages sparsity and the emergence of structured patterns of connectivity. Finally, a learning rate factor, r, is added to Equation 4, which serves as a key free parameter of interest.

Input / output clamping explained by chatty.
I still don’t fully get it, since I only had time to skim rn; it seems artificial.