Learning to Act through Evolution of Neural Diversity in Random Neural Networks

year: 2023
paper: https://arxiv.org/pdf/2305.15945.pdf | https://www.semanticscholar.org/reader/2988ab693f241cf3279438f92ec4054815588260
website: talk snippet; few mins
code: https://github.com/Joachm/neural_diversity_nets
connections: neuronal diversity, biologically inspired, Sebastian Risi, ITU Copenhagen

---

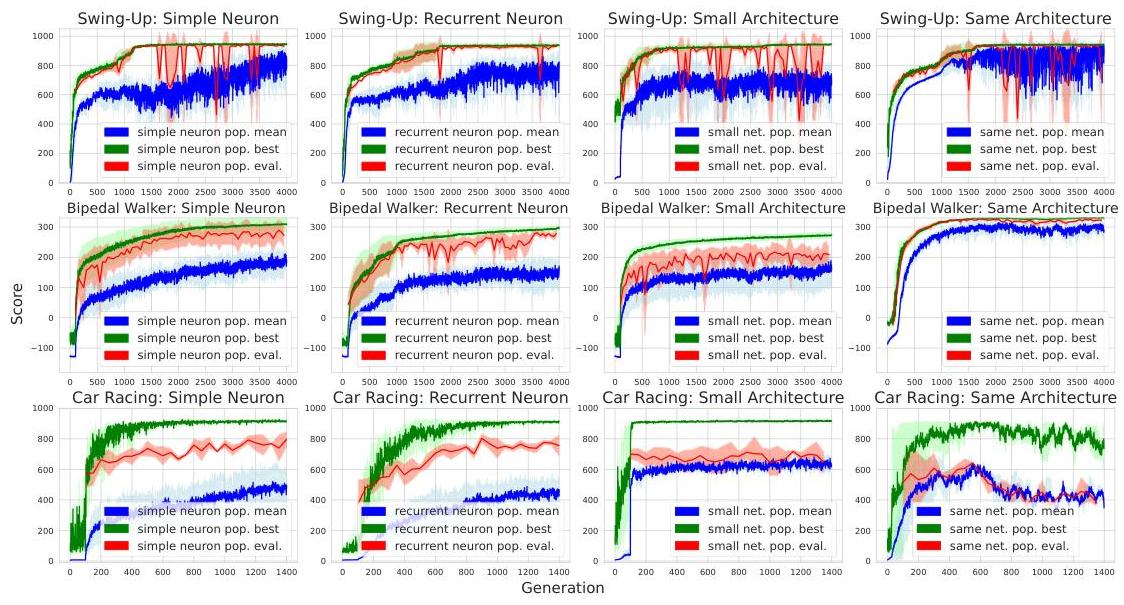
Instead of optimizing synapse weights, they learn more complex (+ recurrent) neuron functions, while keeping a static, randomly initialized set of weights.
The resulting networks have far fewer parameters than a standard FFN with the same structure, and perform competitively or better.
They’re more biologically inspired and allow for interesting extensions.

Motivation

Information in neural networks spreads through many synapses and converges at neurons. Given that a single biological neuron is a sophisticated information processor in its own right, it might be useful to reconsider the extreme abstraction of a neuron as being represented by a single scalar, and an activation that is shared with all other neurons in the network. By parameterizing neurons to a larger degree than current common practice, we might begin to approach some of the properties that biological neurons are characterized by as information processors.
…
We believe that more expressive neural units like the ones proposed here could be useful in combination with online synaptic activity-dependent plasticity functions.

Relation to Weight Agnostic Neural Networks

In their weight agnostic neural network (WANN) work, Gaier and Ha used NEAT to find network structures that could perform well, even when all weights had the same value. Notably, hidden neurons could be evolved to have different activation functions from each other. This likely extended the expressiveness of the WANNs considerably. Our work is similar in spirit to that of Gaier and Ha, in that we are also exploring the capabilities of a component of neural networks in the absence of traditional weight optimization. However, in our work, all networks have a standard fully connected structure. Furthermore, we do not choose from a set of standard activation functions, but introduce stateful neurons with several parameters to tune for each neuron.

$$[{\hat{x}}_{l,i}^t,h_{l,i}^t]=\tanh ({\mathbf{n}}_{l,i}\cdot [x_{l,i}^t,h_{l,i}^{t-1},1{]}^T).$$

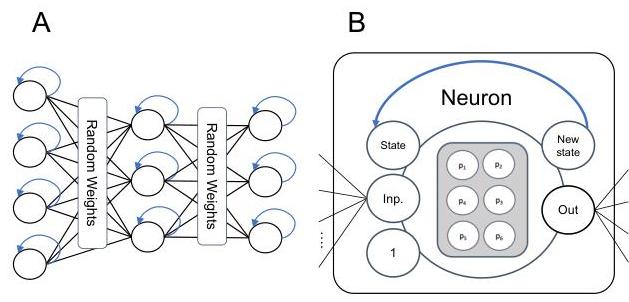
Here, $x_{l,i}^t$ is the input value, $h_{l,i}^{t-1}$ is the state of the neuron, and ${\mathbf{n}}_{l,i}$ the matrix of neural parameters, with $l$ denoting the current layer in the network, $i$ the placement of the neuron in the layer, and $t$ is the current time step. The hyperbolic tangent function is used for non-linearity and to restrict output values to be in $[-1,1]$. ${\hat{x}}_{l+1,j}^t$ is the value that is propagated through weights connecting to the subsequent layer ¹, and $h_{l,i}^t$ is the updated state of the neuron. As the three-by-two matrix has six values in total, we need to optimize six parameters for each neuron in the network.

→ local recurrent states; computationally cheaper than some other forms of recurrence (and more bio plausible; neurons are small dynamical systems)
→ hidden state is not just a copy of the output of the neuron

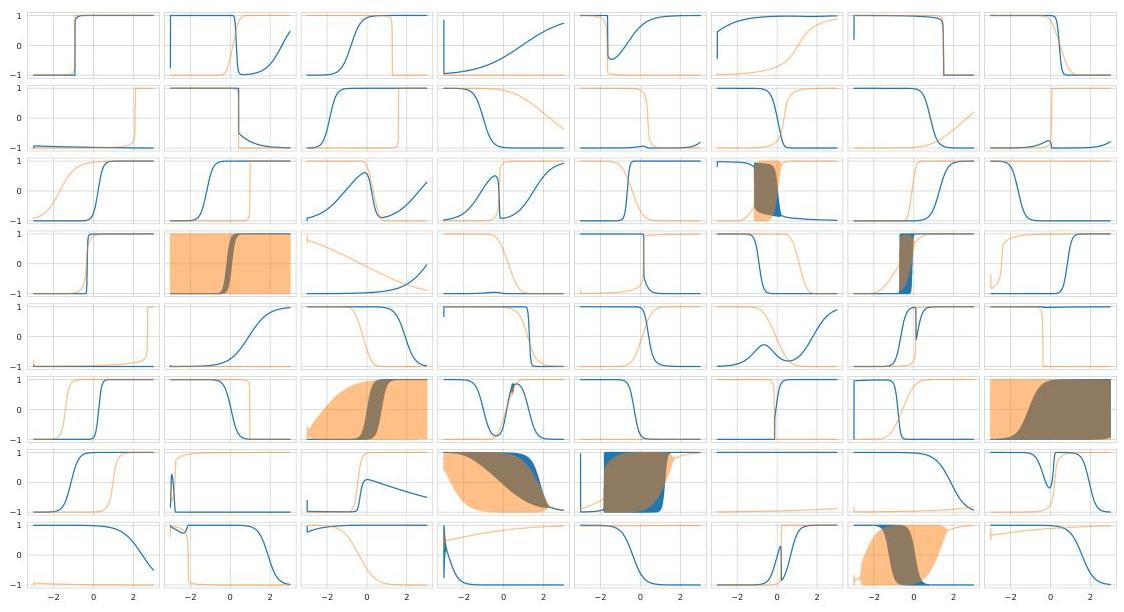
The figure is a “neuron probe.” Each little panel is one neuron from the second hidden layer of a trained/evolved network that plays the CarRacing task.
On the x-axis they sweep an input value from −3 → +3 (1,000 evenly spaced inputs). For each input in that sweep they run the neuron starting from state = 0 at the beginning of the sweep.
Blue line = the neuron’s output/activation that is sent to the next layer.
Orange line = the neuron’s internal state as it evolves while the sweep runs.
Because the neuron has memory, its output isn’t just a static tanh(x); it depends on history/order of inputs during the sweep.

And indeed it works:

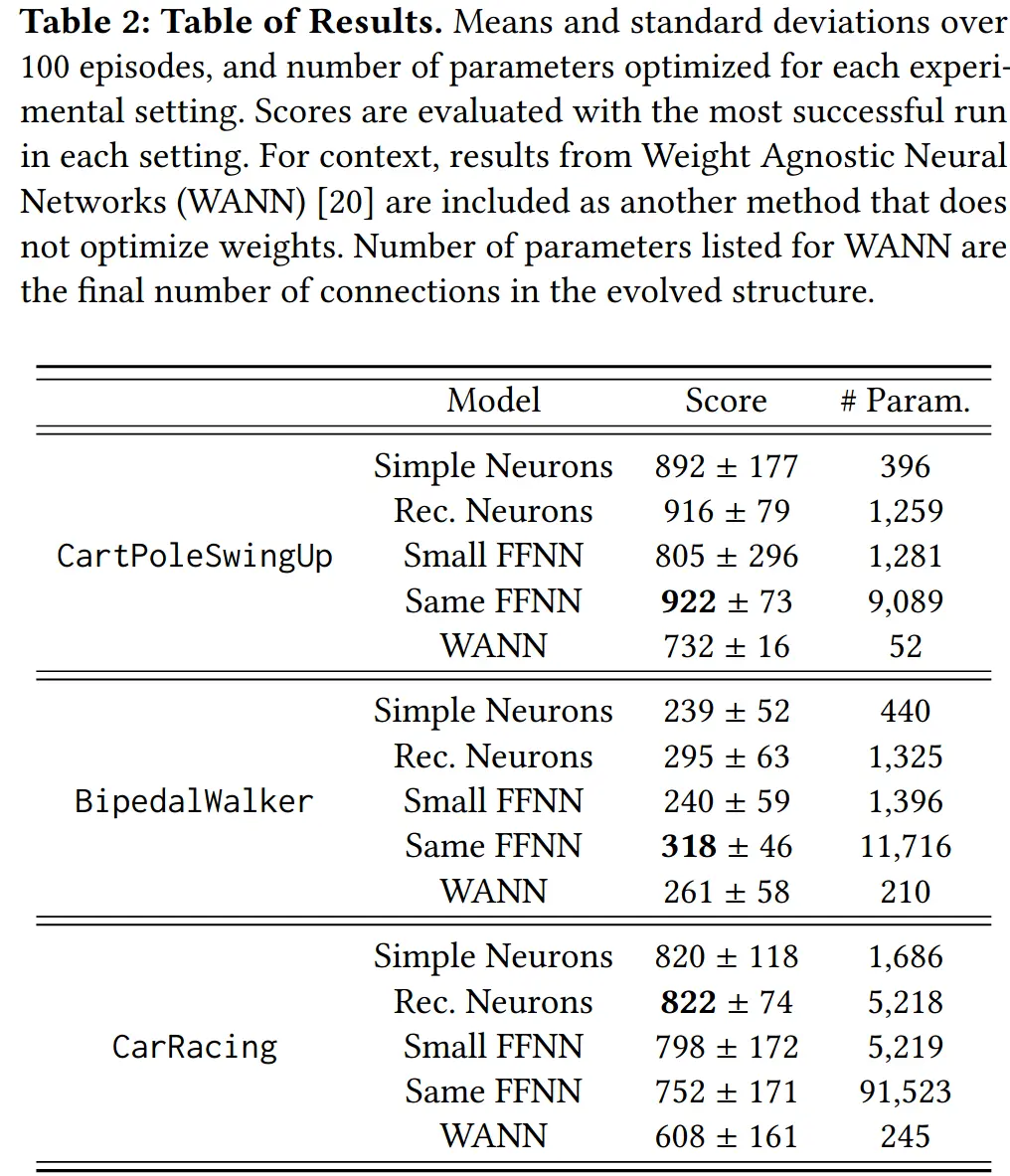
→ It performs better than weight agnostic nets, maybe because it’s harder to learn an arc from scratch.
→ The simple neuron is also their work, but with recurrence removed, and also performs well (→ recurrence not rlly needed for these tasks).

For non-temporal/experiental ML tasks, the recurrence is prlly useless for unordered data.

Why not compare to / combine with LSTM?

Setting up more common recurrent neural networks (RNNs), like LSTMs or GRUs, for the tasks used in this paper, would result in the need for many more adjustable parameters than the number of parameters in the neural units optimized here. [But] Combining stateful neurons with more commonplace RNNs could result in interesting memory dynamics on different timescales.

It is straightforward to incorporate different or more information into the neural units.

Interesting examples of additional information could be reward information from the previous time step or the average activation value of the layer at the previous time step in order to add some lateral information to the neural activation.

If both weights and neurons are optimized together, will there then be as much diversity in the resulting set of neural units, or will the need for such diversity decrease?

---

Activation functions of neurons without recurrence:

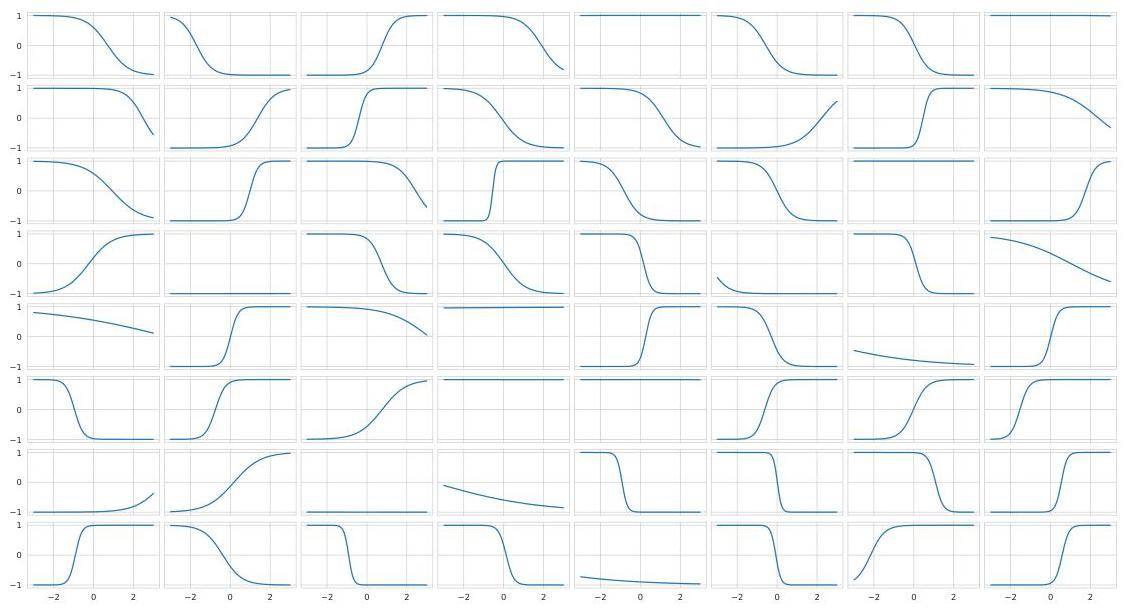
→ Neural activations are either monotonically increasing or decreasing, or unresponsive to the input.

Footnotes

1. $x_{l+1,j}^t={\sum }_i(W_l{)}_{ji}{\hat{x}}_{l,i}^t$, where $W$ is the fixed random synapse weight matrix. ↩