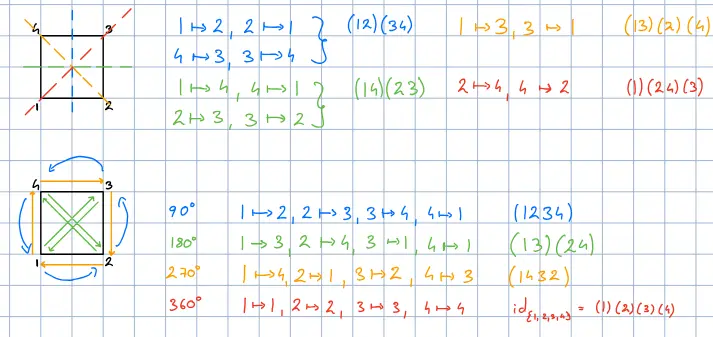TU-Wien ADM Übungen

https://www.dmg.tuwien.ac.at/gittenberger/ADM.pdf
https://vowi.fsinf.at/wiki/TU_Wien:Algebra_und_Diskrete_Mathematik_VO_(Gittenberger)
https://www.dmg.tuwien.ac.at/gittenberger/Folien/GrTh_u_NW.pdf

Last lecture I watched:
2024-11-08 (1:15:00)
Muss auch noch quickly das watchen: https://tuwel.tuwien.ac.at/mod/opencast/view.php?id=2370509&e=9e20ad1d-b7c0-48d6-b0cc-5acc9f3bf7c2

Info

Hinschreiben was Aufgabe ist “z.z.”
Bei der Gleichung kann man auch einfach einen Pfeil mit “IV” zum “=” machen.
Für Übungsbeispiele müssen wir alle darin vorkommenden Definitionen wissen.
Gitti mag kein $0=0$ od $k=k$.
Learn the euclidian algorithm by hand.

Am 2. test wird Wahrscheinlich kommen: Zeige dass $(G\times H,\star )$ eine gruppe ist (kartesische produkt)

Solving a system of equations is also always a testbeispiel

Look at MA Übung 7 (präsenz)

Look at proof of validity for euclid (in the book)

Do 450

Kongruenzrelationen sind Equivalenzrelationen (wie Mal, Plus, Gleichheit, …)

Dijkstra kommt zum zweiten test

There might be some field from ${\mathbb{Z}}_p$ for a vector space at the test.

${\mathbb{R}}^{\mathbb{N}}=\{f:\mathbb{N}\to \mathbb{R}\}$

Übungen:

Induction

Info

Wichtigstes ist, die Induktionsvorraussetzung einzusetzen – sonst ist es keine Induktion.

Aufgabe 1

Man überprüfe die Gleichung

$$1^2+2^2+3^2+\cdots +n^2=\frac{n(n+1)(2n+1)}{6}$$

für die ersten fünf natürlichen Zahlen und beweise sodann deren Gültigkeit für alle natürlichen Zahlen durch vollständige Induktion.

$P(0)=0$ $✓$ Induktionsanfang $⟹\exists n\in \mathbb{N}:1^2+2^2+3^2+\cdots +n^2=\frac{n(n+1)(2n+1)}{6}$ Induktionsvorraussetzung
$P(1)=1$
$P(2)=5$
$P(3)=14$
$P(4)=30$

$\forall n\in \mathbb{N}:P(n)⟹P(n+1)$

$$\begin{array}{rl}{1}^2+2^2+3^2+\cdots +(\boxed{n+1}{)}^2& =\frac{(\boxed{n+1})(\boxed{(n+1)}+1)(2\boxed{(n+1)}+1)}{6}\text{Induktionsbehauptung}\\ & =\frac{(n+1)(n+2)(2n+3)}{6}\\ & \\ & \\ & =\frac{n(n+1)(2n+1)}{6}+(n+1{)}^2\text{Induktionshypothese}\\ & =\frac{n(n+1)(2n+1)}{6}+\frac{6(n+1{)}^2}{6}\text{try to rearrange to behauptung}\\ & =\frac{(n+1)(2n^2+n+6n+6)}{6}\\ & =\frac{(n+1)(n+2)(2n+3)}{6}\text{QED; equals behauptung in line 2}\end{array}$$

Aufgabe 2

Zeige, dass n³ - n für alle n ∈ ℕ stets durch 3 teilbar ist, mittels
(a) eines direkten Beweises,
(b) eines Beweises durch vollständige Induktion.

(a)

$$\begin{array}{r}{n}^3-n=n(n^2-1)=\underset{\text{one of these *3* is divisible by 3}}{\underbrace{(n-1)\cdot n\cdot (n+1)}}\end{array}$$

(b)
$P(0)=0✓$ Induktionanfang $⟹\exists k\in \mathbb{N},\forall n\in \mathbb{N}:n^3-n=3k$ Induktionsvorraussetzung

$$\begin{array}{rl}& (n+1{)}^3-(n+1)\\ =& (n^3+3n^2+3n+1)-(n+1)\\ =& n^3-3n^2+2n\\ =& n(n^2-3n+2)\\ =& \underset{\text{one of these *3* is divisible by 3}}{\underbrace{n(n-1)(n-2)}}\end{array}$$

Alternative formulation bei der Voraussetzung: $3|n^3-n$, oder $n^{3}n\equiv$ 0

Aufgabe 14

Man zeige mittels vollständiger Induktion, dass für die rekursiv definierte Folge $x_1=1$ und
$x_{k+1}=x_k+8k$ für $k\ge 1$ allgemein gilt: $x_n=(2n-1{)}^2$, für alle $n\ge 1$.

$P(1)=1=(2\cdot 1-1{)}^2=1$ $✓$ Induktionsanfang $⟹\forall n\in \mathbb{N}:x_n=(2n-1{)}^2$ Induktionsvorraussetzung

$$\begin{array}{rl}{x}_{n+1}& =x_n+8n\text{recursive def}\\ & =(2n-1{)}^2+8n\text{Induktionsvorraussetzung}\\ & =4n^2-4n+1+8n\\ & =4n^2+4n+1\\ & =(2n+1{)}^2\end{array}$$

Aufgabe 23

$\exists k\in \{0,\dots ,n\},B(k)⟹\forall k\in \{1,\dots ,n\}:B(n)$
(“wenn einer blond ist sind alle blond”)

---

UE1 Gruppenbeispiel

Beweisen Sie mit mittels vollständiger Induktion, dass $\forall n\ge 2:n^2+9n<8^n$

IV: $\exists n:n^2+9n<8^n$
IA: $P(2)=4+18<64$ True

Lösungsweg 1:

$$\begin{array}{r}{8}^{n+1}>8^n\cdot 8\underset{\text{Induktion}}{\underbrace{>}}8\cdot (n^2+9n)>8n^2+72n>n^2+11n+10=(n+1{)}^2+9(n+1)\end{array}$$

($72n>11n+10$)

$$\begin{array}{rl}\text{IV:}& 61n>10n\ge 2\\ \text{IB:}& 61(n+1)>10\\ & 61n+61>\underset{\text{Induktionsvorraussetzung}(61n>10)}{\underbrace{10}}+61>10\end{array}$$

Lösungsweg 2: (verständlicher)

$$\begin{array}{rl}(n+1{)}^2+9(n+1)& =n^2+2n+1+9n+9\\ & =\underset{\text{IV}}{\underbrace{(n^2+9n)}}+2n+10\\ & =8^n+2n+10\end{array}$$

Now we see that $2n+10$ is definitely smaller than $8^n$, and we can put $8^n$ in its place to show that:

$$8^n+8^n<8^{n+1}$$

Since if this is smaller, then the smaller thing is definitely smaller:

$$\begin{array}{r}2\cdot 8^n<8\cdot 8^n\end{array}$$

$✓$

Algebra

Aufgabe 27

Zeigen Sie, dass $\sqrt{6}$ irrational ist.

Assumption that $\sqrt{6}$ is rational:

$$\exists a\in \mathbb{Z},b\in \mathbb{N}\left(b\ne 0\wedge \gcd (a,b)=1\wedge \sqrt{6}=\frac{a}{b}\right)$$

(checking for coprime to specify that it is the simplest form; unique)
Squaring $a,b$ shouldn’t change their divisibility:

$$\begin{array}{rl}\sqrt{6}& =\frac{a}{b}\\ 6& =\frac{a^2}{b^2}\\ 6b^2& =a^2\end{array}$$

$⟹2\mid a,3\mid a⟹\exists k\in \mathbb{Z}:a=6k$
Substituting 6k for a:

$$\begin{array}{rl}6b^2& =(6k{)}^2\\ 6b& =36k^2\\ b^2& =6k^2\end{array}$$

$⟹2\mid b,3\mid b⟹\gcd (a,b)=2⟹\sqrt{6}\notin \mathbb{R}$

Aufgabe 57

Man bestimme zwei ganze Zahlen $x,y$, welche die Gleichung $243x+198y=9$.

bezout’s identity:

$$\gcd (243,198)=243x+198y$$

$\gcd (243,198)$:

$$\begin{array}{rl}243& =q_0\cdot 198+r_0⟹q_0=1,r_0=45\\ 198& =45\cdot q_1+r_1⟹q_1=4,r_0=18\\ 45& =18\cdot q_2+r_2⟹q_2=2,r_2=\boxed{9}\\ 18& =9\cdot q_3+r_3⟹q_3=2,r_3=0\end{array}$$

Backtracking the above steps starting with the second to last line:

$$\begin{array}{rlr}9& =45-2\cdot 18& \text{(From (3))}\\ & =45-2\cdot (198-4\cdot 45)& \text{(From (2))}\\ & =9\cdot 45-2\cdot 198& \\ & =9\cdot (243-1\cdot 198)-2\cdot 198& \text{(From (1))}\\ & =9\cdot 243-11\cdot 198& \end{array}$$ $$\therefore x=9,y=-11$$

Congruences and rest classes

Aufgabe 62a

Beweisen Sie, dass man in einer Kongruenz einen gemeinsamen Faktor der Kongruenzgleichung und des Moduls kürzen kann, d.h. für $c\ne 0$ folgt aus $ac\equiv bc\mathrm{mod}mc$, dass $a\equiv b\mathrm{mod}m$. Gilt auch umgekehrt, dass aus $a\equiv b\mathrm{mod}m$ immer $ac\equiv bc\mathrm{mod}mc$ folgt, falls $c\ne 0$?

$c\ne 0$
1)

$$\begin{array}{rl}ac\equiv bc\mathrm{mod}mc& ⟺\exists k\in \mathbb{Z}:bc-ac=kmc\\ & ⟺\exists k\in \mathbb{Z}:c(b-a)=kmc\\ & ⟺\exists k\in \mathbb{Z}:b-a=km\\ & ⟺a\equiv b\mathrm{mod}m\end{array}$$

$$\begin{array}{rl}a\equiv b\mathrm{mod}m& ⟺\exists k\in \mathbb{Z}:b-a=km\\ & ⟺\exists k\in \mathbb{Z}:c(b-a)=kmc\\ & ⟺\exists k\in \mathbb{Z}:bc-ac=kmc\\ & ⟺ac\equiv bc\mathrm{mod}mc\end{array}$$

Aufgabe 62b

Zeigen Sie, dass beim Rechnen mit Kongruenzen Zahlen immer durch kongruente Zahlen ersetzt werden dürfen, d.h., falls $a+b\equiv c\mathrm{mod}m$ und $b\equiv d\mathrm{mod}m$, dann gilt $a+d\equiv c\mathrm{mod}m$.

Z.Z.: $b\equiv d\mathrm{mod}m,a+b\equiv c\mathrm{mod}m⟹a+d\equiv c\mathrm{mod}m$

$$\begin{array}{rl}a+b\equiv c\mathrm{mod}m& ⟺\exists k_1\in \mathbb{Z}:(a+b)-c=k_{1}m\\ b\equiv d\mathrm{mod}m& ⟺\exists k_2\in \mathbb{Z}:b-d=k_{2}m\\ & ⟺b=d+k_{2}m\\ (a+b)-c=k_{1}m& ⟺(a+(d+k_{2}m))-c=k_{1}m\\ & ⟺(a+d)-c+k_{2}m=k_{1}m\\ & ⟺(a+d)-c=(k_1-k_2)m\\ & ⟺(a+d)-c=k_{3}m,\text{ where }{k}_3=k_1-k_2\in \mathbb{Z}\\ & ⟺a+d\equiv c\mathrm{mod}m\end{array}$$

AUfgabe 64–69 Bestimmen Sie alle L¨osungen der folgenden Kongruenzen bzw. beweisen Sie die Unl¨osbar-

keit (in $\mathbb{Z}$).

Aufgabe 64a

$8x\equiv 4\mathrm{mod}16$

$$\begin{array}{rl}4-8x& =16k\\ 1-2x& =4k\\ \underset{\text{even}}{2x}& =\underset{\text{odd}}{4k+1}\end{array}$$

64b

$8x\equiv 4\mathrm{mod}15$

$\gcd (8,4)=4$
$\gcd (4,15)=1$ (check for divisibility in the congruence)
$8x\equiv 4\mathrm{mod}15⟺2x\equiv 1\mathrm{mod}15⟺1-2x=15k⟺2x+15k=1$

extended euclidian algorithm:

a	b	q	r	k	x
15	2	7	1	1	-7
2	1	2	0	0	1
$2\cdot -7+15\cdot 1=1$ $✓$
$⟹x_1=-7,k_1=1$

Make positive: $x_1+=15⟹x_1=8$
Check:
$8\cdot x_1\equiv 8\mathrm{mod}15$
$4-8\cdot 8=-60$, which is divisible by 15 $✓$

Alternative Lösung:

$2\cdot 8^{-1}\cdot 8x\equiv 8^{-1}\cdot 2\cdot 4$ (15) ($|\cdot 2\cdot 8^{-1}$ – geht, weil $\gcd (8,15)=1$)
$2x\equiv 1\mathrm{mod}15⟺15+1\mid 2x⟹x_1=8$

UE3 Gruppenbeispiel:

Der EAN-Code besteht aus 13 Bezimalziffern, ist also von der Form $a_1,a_2,\dots a_{12},a_{13}$, wobei die Ziffern die Kongruenz $a_1+3a_2+a_3+3a_4+\cdots +a_{11}+3a_{12}+a_{13}\equiv 0\mathrm{mod}10$ erfüllen müssen. Beweisen Sie, dass ein Fehler (1) in einer einzelnen (1) Ziffer stets erkannt wird! ($a_{13}\dots$ Prüfziffer)

Todo

we exchange some $a_i$ for some $b\ne a_i$
$s+n{a}_i\equiv 0\mathrm{mod}10$
$s+nb\equiv 0\mathrm{mod}10$

$$s_1=\sum _{j=1,2j-1\ne i}^7{a}_{2,j-1}$$ $$s_2=\sum _{k=1,2k\ne i}^6$$

$n{a}_i+s_1+s_2=n_{b_i}+s_1+s_2\mathrm{mod}10$
$na=n{b}_i\mathrm{mod}10$
$⟹0\le a_i=b_i\mathrm{mod}10$

gg(1,10) = 1
ggt(3, 10) = 1

$a_i-b_i=10k⟺b_i\mathrm{mod}10$

Complex numbers

Aufgabe 34

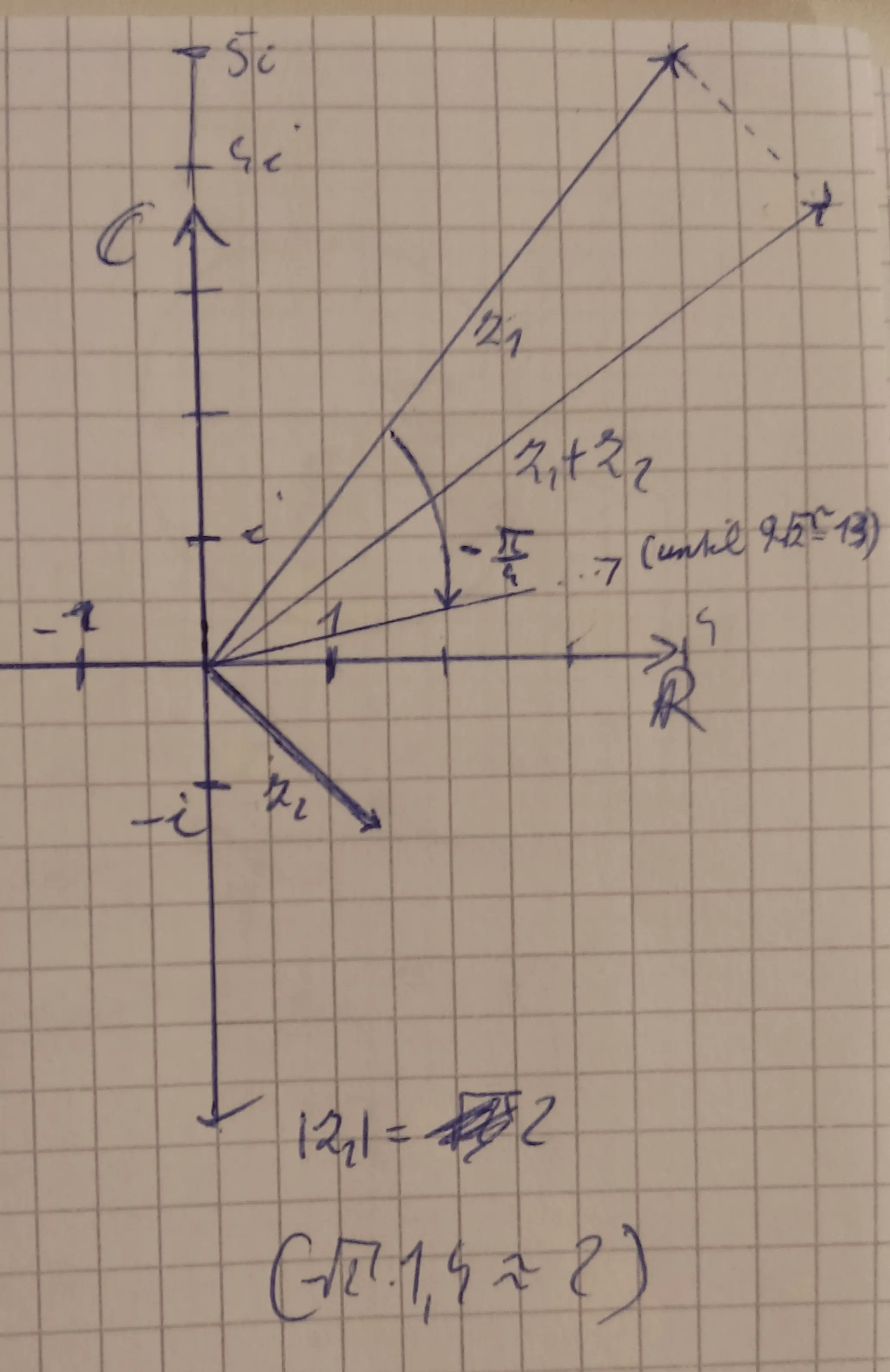
Man bestimme rechnerisch (ohne Taschenrechner) und graphisch Summe und Produkt der
komplexen Zahlen für $z_1=4+5i$ und $z_2=[2,-\frac{\pi }{4}]$.

Finding out $x,y$ for $z_2$:

$$\begin{array}{rl}{z}_2& =x+iy\\ \mid z_2\mid & =x^2+(iy{)}^2=2^2\\ & =\sqrt{x^2-y^2}=2\\ & ⟹x=\sqrt{2},y=-\sqrt{2}\end{array}$$

→ $z_2=\sqrt{2}-\sqrt{2}i$
Sum:

$$z_1+z_2=4+\sqrt{2}+(5-\sqrt{2})i$$

Product:

$$\begin{array}{rl}(4+5i)\cdot (\sqrt{2}-\sqrt{2}i)& =4\sqrt{2}+5\sqrt{2}i-4\sqrt{2}i+5\sqrt{2}\\ & =9\sqrt{2}+\sqrt{2}i\end{array}$$

Aufgabe 46

Man beschreibe die Menge jener komplexen Zahlen $z$, die $\Re (\frac{z-a}{b})>0$ erfüllen ($a,b\in \mathbb{C}$, $b\ne 0$), geometrisch.

Multiplikation mit einer komplexen Zahl ist eine Dreh-Streckung, außer der Betrag ist $1$, dann ist es nur eine Drehung.
Mit der konjugiert-komplexen zahl kann man spiegeln.

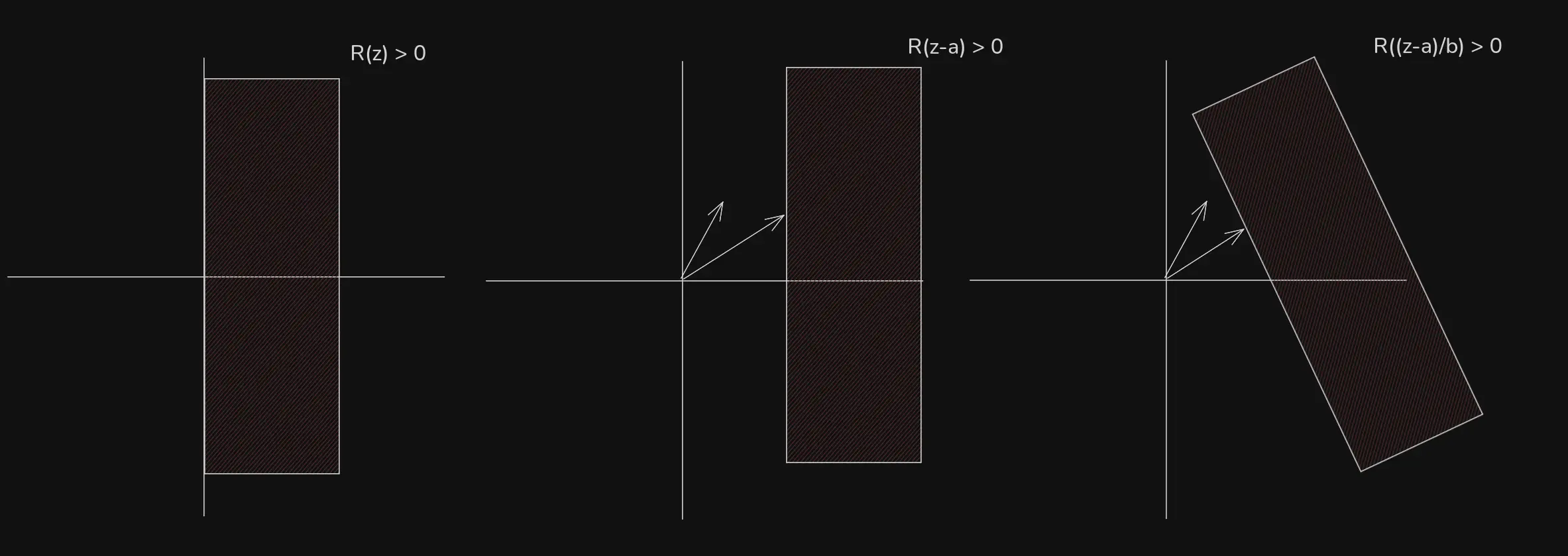
Das bsp kann man auch iwie mit zahlen zeigen but idk how.

“Man kann einsetzen und rechnen, ist aber mühsam”

UE2 Gruppenbeispiel

Stelllen Sie alle Lösungen der quadratischen gleichung $z^2+2z+4=0$ sowohl in der Form $a+bia,b\in \mathbb{R}$, als auch in der Polarkoordinatenform $r(\cos \varphi +i\sin \varphi )r\ge 0,0\le \varphi <2\pi$ dar.

$z=a+bi$
$z_{1,2}=1\pm \sqrt{1^2-4}$
$z_{1,2}=-1\pm i\sqrt{3}$

For some reason we need to add pi or sth to the angle

Using calculator:
$z_{1,2}=-1\pm i\sqrt{3}$
$\mid z\mid =\sqrt{1+3}=2$
$\theta =\arctan \left(\pm \sqrt{3}\right)=\pm \frac{\pi }{3}$
$z_{1,2}=2\cdot (\cos$

Logic

Aufgabe 78-83

Entscheiden Sie mit Hilfe einer Wahrheitstafel, ob die folgenden ¨Aquivalenzen richtig sind.
→ und ↔ bezeichnen Sub- bzw. Bijunktion.

Aufgabe 80

$a\wedge (b\vee c)⟺(a\wedge b)\vee (a\wedge c)$

a	b	c	$a\wedge (b\vee c)$	$a\wedge b$	$a\wedge c$	$(a\wedge b)\vee (a\wedge c)$
0	0	0	0	0	0	0
0	0	1	0	0	0	0
0	1	0	0	0	0	0
0	1	1	0	0	0	0
1	0	0	0	0	0	0
1	0	1	1	0	1	1
1	1	0	1	1	0	1
1	1	1	1	1	1	1

The equivalence is true.

sets

92–100) Beweisen Sie die folgenden Beziehungen mit Hilfe von Elementtafeln oder geben Sie ein konkretes Gegenbeispiel an.

Aufgabe 99

$A\cap (B△C)=(A\cap B)△(A\cap C)$

NOTE: $0$ is used for $\notin$, $1$ for $\in$ for ease of writing…

A	B	C	$B△C$	$A\cap (B△C)$	$A\cap B$	$A\cap C$	$(A\cap B)△(A\cap C)$
0	0	0	0	0	0	0	0
0	0	1	1	0	0	0	0
0	1	0	1	0	0	0	0
0	1	1	0	0	0	0	0
1	0	0	0	0	0	0	0
1	0	1	1	1	0	1	1
1	1	0	1	1	1	0	1
1	1	1	0	0	1	1	0

→ Richtige Beziehung.

relations

Aufgabe 109

Man zeige, dass durch

$$aRb\iff 3|a^2-b^2\text{ fu¨r alle }a,b\in \mathbb{Z}$$

eine Äquivalenzrelation $R$ in der Menge $\mathbb{Z}$ erklärt wird, und bestimme die zugehörende Partition.

Reflexivity:

$$aRa⟺3\mid (a^2-a^2)⟺3\mid 0✓$$

Symmetric:

$$\begin{array}{rl}aRb& ⟺bRa\\ 3\mid a^2-b^2& ⟺3\mid -(b^2-a^2)\end{array}$$

$✓$
Transitive: (aRb, bRc → aRc)

$$\begin{array}{rl}3\mid (a^2-b^2)& \wedge 3\mid (b^2-c^2)\\ a^2-b^2=3k& \wedge b^2-c^2=3m\end{array}$$

$a^2-c^2=(a^2-b^2)+(b^2-c^2)=3k+3m=3(k+m)$ $✓$

---

$p=\{r+3k\mid k\in \mathbb{Z},r\in \{0,1,2\}\}=\{{\bar{0}}_3,{\bar{1}}_3,{\bar{2}}_3\}$
$\forall a,b\in p_i:3\mid a^2-b^2$

Aufgabe 114–118)

Stellen Sie die folgenden Relationen im kartesischen Koordinatensystem und auch als gerichteten Graphen dar und untersuchen Sie weiters, ob eine Äquivalenzrelation vorliegt.

Aufgabe 114

Die Relation $R$ sei für $m,n\in \{2,3,4,5\}$ definiert durch $mRn\iff m+n$ ungerade oder $m=n$.

Self-loops: reflexive
Edges in both directions: symmetric
Every edge can be reached from any other: transitive

Aufgabe 123

Sei $T_{70}$ die Menge aller natürlichen Zahlen, die 70 teilen. Man vergleiche die Hassediagramme der beiden Halbordnungen $(\mathbb{P}(\{a,b,c\}),\subseteq )$ und $(T_{70},|)$.

Warum sind die beiden graphen isomorph?

UE4 Gruppenbeispiel

Let $M=\{(a,b)\in \mathbb{Z}\times \mathbb{Z}\mid b\ne 0\}$, $N=\mathbb{Z}\times \mathbb{Z}$
$R=\{((m,n),(x,y))\in M\times M\mid my=nx\}$
$S=\{((m,n),(x,y))\in N\times N\mid ny=nx\}$

$R$ ist for sure equivalenzrelation
$S$ does not fulfill transitivity.

functions

Aufgabe 136-140

Untersuchen Sie, ob es sich bei den folgenden Relationen $R\subseteq A\times B$ um Funktionen, injektive Funktionen, surjektive Funktionen bzw. bijektive Funktionen handelt. (${\mathbb{R}}^{+}$ bezeichnet die Menge aller positiven reellen Zahlen.)

Aufgabe 136

$R=\{(\sqrt{x},\frac{1}{x})|x\in {\mathbb{R}}^{+}\},A=B={\mathbb{R}}^{+}$

Assumption: $0\notin {\mathbb{R}}^{+}$

$R_f=\{x,f(x)\mid x\in A\}$
$\sqrt{x}\mapsto \frac{1}{x}$
$x\mapsto \frac{1}{x^2}$
$f(x)=\frac{1}{x^2}$

Injective: $f(x)=f(y)⟹x=y$
$\forall x,y\in {\mathbb{R}}^{+}:\frac{1}{x^2}=\frac{1}{y^2}⟹x=y$ $✓$
Surjective: $\forall y\in B,\exists x\in A:f(x)=y$
$\forall y\in {\mathbb{R}}^{+},\exists x\in {\mathbb{R}}^{+}:\frac{1}{x^2}=y⟹x=\sqrt{\frac{1}{y}}$ $✓$
Bijective: jo

Aufgabe 145

Seien $f:A\to B$ und $g:B\to C$ Abbildungen. Zeigen Sie, dass aus der Surjektivität von $g\circ f$ die Surjektivität von $g$ und aus der Injektivität von $g\circ f$ die Injektivität von $f$ folgt.

$f:A\to B,g:B\to C$, $g\circ f=g(f(x))$
$g\circ f$ surjective $⟹g$ surjective

$$\begin{array}{r}\forall c\in C\exists a\in A:g(f(a))=c⟹\forall b\in B\exists c\in C:g(b)=c\end{array}$$

$g\circ f$ injective $⟹f$ injective

$$\begin{array}{r}\forall a_1,a_2\in A,a_1\ne a_2:g(f(a_1))\ne g(f(a_2))⟹f(a_1)\ne f(a_2)\end{array}$$

Combinatorics

Aufgabe 162

Wieviele „Wörter” der Länge 28 gibt es, bei denen genau 5-mal der Buchstabe a, 14-mal b, 5-mal c, 3-mal d vorkommen und genau einmal e vorkommt?

$W=\{a^5,b^{14},c^5,d^3,e^1\}$
$|W|=28$
$\#\text{perm}(W)=\frac{27!}{5!\cdot 14!\cdot 5!\cdot 3!}$

Aufgabe 196

In einer Menge von $n$ Personen können 10 Personen Deutsch, 9 Englisch, 9 Französisch, 5 Deutsch und Englisch, 7 Deutsch und Französisch, 4 Englisch und Französisch, 3 alle drei Sprachen und niemand keine der drei Sprachen. Wie groß ist $n$?

$n=|D\cup E\cup F|=|D|+|E|+|F|-|D\cap E|-|D\cap F|-|E\cap F|+|D\cap E\cap F|=25$
(assuming the language speakers were listed in overlapping form… else it would just be the sum of all the multiplicities mentioned in the problem statement)

Test aufgabe (Maze)

Solution + problem statement: https://chatgpt.com/c/674449b4-7ef0-800f-8247-d5777331bb71

3 up, 3 rechts $\left(\genfrac{}{}{0ex}{}{6}{(3,3)}\right)$

Du hattest eine unglaublich schöne Lösung. Was ist dein Lieblingsgemüse?

Gelöst durch rekursion od Pascals Dreieck

Graph Theory

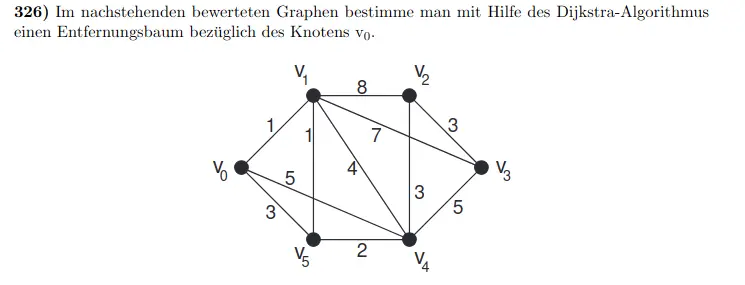
Aufgabe 326

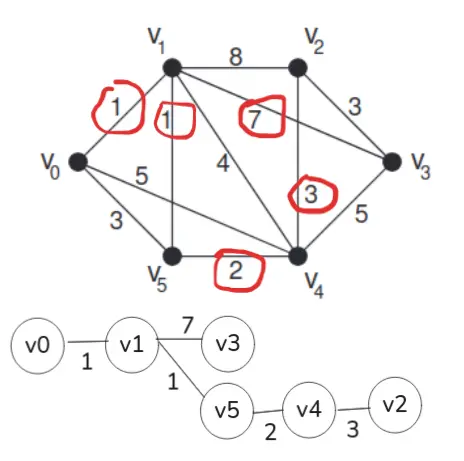
Algebra

Aufgabe 338

Man zeige, dass $(\mathbb{Z},\bullet )$ mit der Operation

$$a\bullet b=a+b-ab,\forall a,b\in Z$$

eine Halbgruppe ist. Gibt es ein neutrales Element? Wenn ja, welche Elemente haben Inverse?

Closure: $✓$ (since $\pm ,\cdot$ are closed in $\mathbb{Z}$)

i)

Definition: $(\mathbb{Z},\bullet )$ is eine Halbgruppe $⟺\forall a,b,c\in \mathbb{Z}:a\bullet (b\bullet c)=(a\bullet b)\bullet c$

$\forall a,b,c\in \mathbb{Z}$:

$$\begin{array}{rl}a\bullet (b\bullet c)& =(a\bullet b)\bullet c\\ a\bullet (b+c-bc)& =(a+b-ab)\bullet c\\ a+b+c-bc-(ab+ac-abc)& =(a+b-ab)+c-c(a+b-ab)\\ a+b+c-ab-bc-ac+abc& =a+b+c-ab-ac-bc+abc\end{array}$$

$⟹$ Halbgruppe

ii)
Definition: $(\mathbb{Z},\bullet )$ hat ein neutrales element $⟺\forall a\in \mathbb{Z}:\exists e\in \mathbb{Z}:e\bullet a=a\bullet e=a$

$$\begin{array}{rl}a\bullet b& =a\\ a+b-ab& =a\\ b-ab& =0\\ b(1-a)& =0\\ b& =0\vee a=1\end{array}$$

$⟹$ Neutrales Element: $0$
$⟹$ Identität: $1$

iii)
Definition: $(\mathbb{Z},\bullet )$, $a\in \mathbb{Z}$ hat ein inverses element $⟺\exists b:a\bullet b=0$

$$\begin{array}{rl}a\bullet b& =0\\ a+b-ab& =0\\ b-ab& =-a\\ b(1-a)& =-a\\ b& =\frac{-a}{1-a}\\ b& =\frac{a}{a-1}\end{array}$$

NOTE: A better version would be to rearrange to $(a-1)\cdot (b-1)+1=1$ $⟹$ $a-1\mid 1,b-1\mid 1⟹$ both are $\pm 1$

Aufgabe 366

Man zeige: Eine nichtleere Teilmenge $U$ einer Gruppe $G$ (mit neutralem Element $e$) ist genau dann Untergruppe von $G$, wenn
$(i)a,b\in U⟹ab\in U,(ii)e\in U,(iii)a\in U⟹a^{-1}\in U$

Definition of a sub.

i)

$$\begin{array}{rl}a,b\in U& ⟹ab\in U\\ & ⟹c\in U⟹abc\in U\\ & ⟹a(bc)\in U\wedge (ab)c\in U\\ & ⟹\text{Associativity \& Closure}\end{array}$$

ii)

$$\begin{array}{rl}e\in U& ⟹e\cdot e=e\in U\end{array}$$

Neutrales Element

iii)

$$\begin{array}{rl}a\in U& ⟹a^{-1}\in U\\ & ⟹a\cdot a^{-1}=e\in U\end{array}$$

Aufgabe 373

Note: The brackets are the cycle notation of permutations!

UE6 Gruppenbeispiel

Sei $U\le G$ “Normalteiler” (alle links und rechtsnebenklassen stimmen überein) von $(G,\circ )$. Sei $R\subseteq G\times G$. Zeigen sie $x,y\in G,xRy⟺xU=Uy$ ist Äquivalenzrelation.

reflexiv: $xRx⟺xU=Ux$ (aus Definition von Normalteliler)
symmetric: $xRy⟺yRx$, $xU=Uy=yU$
transitive: $(xRy\wedge yRz⟹xRz)⟹xRz$: $xU=Uy,yU=uz,xU=Uz$

$$3\cdot N\cdot \frac{1}{3}=N$$ $$U\text{ Normalteiler}:\forall x\in G:x\circ U=U\circ x$$

Kommutative Gruppen sind immer Normalteiler

Aufgabe 399)

Von der Abbildung $f:({\mathbb{Z}}_3{)}^2\to ({\mathbb{Z}}_3{)}^4$ sei bekannt, dass $f$ ein Gruppenhomomorphismus bezüglich der Addition ist (die jeweils komponentenweise definiert sein soll), sowie dass $f(0,1)=(0,1,1,2)$, $f(1,0)=(1,0,2,0)$. Man ermittle daraus $f(w)$ für alle $w\in ({\mathbb{Z}}_3{)}^2$.

$({\mathbb{Z}}_3{)}^2$ denotes the two-dimensional vector space over the field ${\mathbb{Z}}_3$. Correction: No it does not (say that in the Angabe), you can think of it like that, but ${\mathbb{Z}}_3\times {\mathbb{Z}}_3$ is still just a group. But it still works just as well due to homomorphism properties.
Each element is an ordered pair $(a,b)$ where $a,b\in {\mathbb{Z}}_3=\{0,1,2\}$, with addition performed componentwise modulo 3.
The space contains a total of 9 elements:

$$\begin{array}{rl}({\mathbb{Z}}_3{)}^2& =\{(a,b)\mid a,b\in {\mathbb{Z}}_3\}\\ ({\mathbb{Z}}_3{)}^2& =\{(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)\}\end{array}$$

$({\mathbb{Z}}_3{)}^4$ is the four-dimensional vector space over ${\mathbb{Z}}_3$. Each element is a 4-tuple $(a,b,c,d)$ where $a,b,c,d\in {\mathbb{Z}}_3=\{0,1,2\}$, with addition performed componentwise modulo 3. The space contains $3^4=81$ elements in total.

For instance, adding two elements in $({\mathbb{Z}}_3{)}^2$: $(1,2)+(2,2)=(1+2\mathrm{mod}3,2+2\mathrm{mod}3)=(0,1)$

This is because $1+2=3\equiv 0(\mathrm{mod}3)$ and $2+2=4\equiv 1(\mathrm{mod}3)$.

For a group homomorphism we know that for any vectors $v,w$ and scalar $c$:

$$\begin{array}{rl}f(v+w)& =f(v)+f(w)\text{ (preserves addition)}\\ f(cv)& =cf(v)\text{ (preserves scalar multiplication)}\end{array}$$

Any vector $(a,b)\in ({\mathbb{Z}}_3{)}^2$ can be written as a linear combination of the standard basis vectors $(1,0)$ and $(0,1)$:

$$(a,b)=a(1,0)+b(0,1)$$

Now we can solve:

For any $w=(a,b)\in ({\mathbb{Z}}_3{)}^2$:

$$\begin{array}{rl}f(w)& =f(a,b)\\ & =f(a(1,0)+b(0,1))\\ & =f(a(1,0))+f(b(0,1))\text{ (homomorphism preserves addition)}\\ & =af(1,0)+bf(0,1)\text{ (homomorphism preserves scalar multiplication)}\\ & =a(1,0,2,0)+b(0,1,1,2)\text{ (given values)}\\ & =(a,0,2a,0)+(0,b,b,2b)\\ & =(a,b,2a+b,2b)\end{array}$$

This gives us a formula for $f(w)$ for any input $w=(a,b)$, where all calculations are performed modulo 3.

We can verify this works for our given values:

For $w=(1,0)$: $f(1,0)=(1,0,2,0)$ ✓
For $w=(0,1)$: $f(0,1)=(0,1,1,2)$ ✓

Aufgabe 424)

Sei $(R,+,\cdot )$ ein Ring mit Einselement und $E(R)$ die Menge derjenigen Elemente in $R$, die bezüglich der Multiplikation ein inverses Element besitzen. Zeigen Sie, dass $E(R)$ mit der Multiplikation eine Gruppe bildet (die Einheitengruppe von $R$).

Einselement means there is a neutral element for multiplication.
For a ring $R$, $E(R)$ is the set of all elements that have a multiplicative inverse:

$$E(R)=\{a\in R\mid \exists b\in R:a\cdot b=b\cdot a=1_R\}$$

These elements are also called the units of $R$.
In this example, $0$ – the absorbing element – does not have a multiplicative inverse, so it is not in $E(R)$.

To show $E(R)$ forms a group under multiplication, we need to verify the four group axioms:

1. Closure: $\forall a,b\in E(R):a\cdot b\in E(R)$
2. Associativity: $\forall a,b,c\in E(R):(a\cdot b)\cdot c=a\cdot (b\cdot c)$
3. Identity: $\forall a\in E(R),\exists 1_R\in E(R):1_R\cdot a=a\cdot 1_R=a$
4. Inverse: $\forall a\in E(R),\exists a^{-1}\in E(R):a\cdot a^{-1}=a^{-1}\cdot a=1_R$

Solution

1) Closure:
Z.z.: $\forall (a\cdot b)\in E(R)⟹(a\cdot b{)}^{-1}\in E(R)$

$$(a\cdot b)(b^{-1}\cdot a^{-1})=a(b\cdot b^{-1})a^{-1}=a\cdot 1_R\cdot a^{-1}=a\cdot a^{-1}=1_R$$

Similarly $(b^{-1}\cdot a^{-1})(a\cdot b)=1_R$.

2) Associativity: Follows from associativity in $R$.

3) Identity: By definition “Ring mit Einselement” (→ $1_R$ is inverse to itself since $1_R\cdot 1_R=1_R$ and $\forall a\in E(R):1_R\cdot a=a\cdot 1_R=a$)

4) Inverse: By definition of $E(R)$ and closure.

Therefore, $E(R)$ forms a group under multiplication. ■

$(ab{)}^{-1}=b^{-1}{a}^{-1}$ Alwayws holds if they are invertible

Doing the closure proof like $(ab)(a^{-1}{b}^{-1})$ would not be valid since the ring does not assume commutativity.

Aufgabe 456)

Bildet ${\mathbb{R}}^2$ mit den angegebenen Operationen einen Vektorraum über $\mathbb{R}$?

$$\begin{array}{rl}(x_1,x_2)+(y_1,y_2)& =(x_1+y_1,0)\\ \lambda (x_1,x_2)& =(\lambda x_1,0)\end{array}$$

Consider the vector $(0,1)\in {\mathbb{R}}^2$. For any scalar $\lambda \in \mathbb{R}$: $\lambda (0,1)=(\lambda \cdot 0,0)=(0,0)$
So the fourth axiom of scalar multiplication is violated:

$$\text{Identity: }1\vec{v}=\vec{v}$$

Übungsbeispiel X

Lösen Sie $\bar{3}x+\bar{2}x+\bar{6}=\bar{0}$ über ${\mathbb{Z}}_7$ mithilfe der quadratischen Lösungsformel.

Let's solve this step by step using the quadratic formula in ${\mathbb{Z}}_7$

First, rearrange into standard form $a{x}^2+bx+c=0$:

$$\begin{array}{rl}\bar{3}{x}^2+\bar{2}x+\bar{6}& =\bar{0}\\ ⟹a{x}^2+bx+c& =0\text{ where }a=\bar{3},b=\bar{2},c=\bar{6}\end{array}$$

The quadratic formula states $x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$. In ${\mathbb{Z}}_7$, we need to find:

$$x=\overline{(-2\pm \sqrt{4-4(3)(6)})}\cdot \overline{(2\cdot 3{)}^{-1}}$$

Computing in ${\mathbb{Z}}_7$

First compute under the square root:
$4-4(3)(6)=4-72\equiv 4-2\equiv 2(\mathrm{mod}7)$

We need to find the square root of 2 in ${\mathbb{Z}}_7$. Testing each element:
$1^2\equiv 1$, $2^2\equiv 4$, $3^2\equiv 2$, $4^2\equiv 2$, $5^2\equiv 4$, $6^2\equiv 1$
Therefore $\sqrt{2}\equiv \pm 3(\mathrm{mod}7)$

Also, we need $(2\cdot 3{)}^{-1}=6^{-1}$ in ${\mathbb{Z}}_7$. Since $6\cdot 6\equiv 1(\mathrm{mod}7)$, we have $6^{-1}\equiv 6$

Putting it all together:

$$\begin{array}{rl}x& =(-2\pm 3)\cdot 6\\ & =(-5\text{ or }1)\cdot 6\\ & \equiv (2\text{ or }1)\cdot 6\\ & \equiv 5\text{ or }6(\mathrm{mod}7)\end{array}$$

Therefore $x\equiv 5(\mathrm{mod}7)$ and $x\equiv 6(\mathrm{mod}7)$ are the solutions.

Let’s verify: For $x\equiv 5$:
$3(5{)}^2+2(5)+6\equiv 3(4)+3+6\equiv 5+3+6\equiv 0(\mathrm{mod}7)$ ✓

For $x\equiv 6$:
$3(6{)}^2+2(6)+6\equiv 3(1)+5+6\equiv 3+5+6\equiv 0(\mathrm{mod}7)$ ✓

462

Untersuchen Sie, ob $W$ ein Teilraum des Vektorraums ${\mathbb{R}}^3$ über $\mathbb{R}$ ist, und beschreiben sie die Menge $W$ geometrisch: $W=\{(x,y,z)\mid x=2y\}$

zZ: $W\le {\mathbb{R}}^3$

$$\begin{array}{rl}& (1)0\in W\text{ (zero vector)}\\ & (2)u,v\in W⟹u+v\in W\text{ (closure under addition)}\\ & (3)\lambda \in \mathbb{R},u\in W⟹\lambda u\in W\text{ (closure under scalar multiplication)}\end{array}$$

$(1)$ Zero vector: For $0=(0,0,0)$, we have $x=0=2y$, so $0\in W$

$(2)$ Addition: Let $u=(x_1,y_1,z_1),v=(x_2,y_2,z_2)\in W$.
Then: $x_1=2y_1$ and $x_2=2y_2$
$u+v=(x_1+x_2,y_1+y_2,z_1+z_2)$
$x_1+x_2=2y_1+2y_2=2(y_1+y_2)$
Therefore $u+v\in W$

$(3)$ Scalar multiplication: Let $u=(x,y,z)\in W$ and $\lambda \in \mathbb{R}$
$x=2y$
$\lambda u=(\lambda x,\lambda y,\lambda z)$
$\lambda x=\lambda (2y)=2(\lambda y)$
Therefore $\lambda u\in W$

Geometric interpretation

$W$ is a plane in ${\mathbb{R}}^3$ passing through the origin. The equation $x=2y$ fixes the relationship between $x$ and $y$ coordinates, while $z$ remains free.
This means $W$ is a plane parallel to the $z$-axis, intersecting the $xy$-plane along the line $x=2y$.

492

B is a basis if it is linearly independent and spans ℝ³:
$\text{span}(B)={\mathbb{R}}^3\text{ and B is linearly independent}$

Solution

Let’s show that the only solution to ${\lambda }_1{v}_1+{\lambda }_2{v}_2+{\lambda }_3{v}_3=0$ is ${\lambda }_1={\lambda }_2={\lambda }_3=0$:

$${\lambda }_1\left(\begin{array}{c}1\\ 2\\ 4\end{array}\right)+{\lambda }_2\left(\begin{array}{c}2\\ 4\\ 1\end{array}\right)+{\lambda }_3\left(\begin{array}{c}4\\ 2\\ 1\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right)$$ $$\begin{array}{rl}& \left(\begin{array}{ccc}1& 2& 4\\ 2& 4& 2\\ 4& 1& 1\end{array}\right)\stackrel{R_2-2R_1}{\to }\left(\begin{array}{ccc}1& 2& 4\\ 0& 0& -6\\ 4& 1& 1\end{array}\right)\\ & \stackrel{R_3-4R_1}{\to }\left(\begin{array}{ccc}1& 2& 4\\ 0& 0& -6\\ 0& -7& -15\end{array}\right)\stackrel{\frac{R_2}{-6}}{\to }\left(\begin{array}{ccc}1& 2& 4\\ 0& 0& 1\\ 0& -7& -15\end{array}\right)\\ & \stackrel{R_3+15R_2}{\to }\left(\begin{array}{ccc}1& 2& 4\\ 0& 0& 1\\ 0& -7& 0\end{array}\right)\stackrel{\frac{R_3}{-7}}{\to }\left(\begin{array}{ccc}1& 2& 4\\ 0& 0& 1\\ 0& 1& 0\end{array}\right)\\ & \stackrel{R_1-4R_2}{\to }\left(\begin{array}{ccc}1& 2& 0\\ 0& 0& 1\\ 0& 1& 0\end{array}\right)\stackrel{R_1-2R_3}{\to }\left(\begin{array}{ccc}1& 0& 0\\ 0& 0& 1\\ 0& 1& 0\end{array}\right)\end{array}$$

This gives us ${\lambda }_1=0$, ${\lambda }_2=0$, and ${\lambda }_3=0$. Therefore, B is linearly independent.
Shorter version:

$$\left(\begin{array}{ccc}1& 2& 4\\ 2& 4& 2\\ 4& 1& 1\end{array}\right)\to \left(\begin{array}{ccc}1& 2& 4\\ 0& 0& -6\\ 0& -7& -15\end{array}\right)\to \left(\begin{array}{ccc}1& 2& 4\\ 0& 1& \frac{15}{7}\\ 0& 0& 1\end{array}\right)$$

Oooor:

$$\begin{array}{rl}\det \left(\begin{array}{ccc}1& 2& 4\\ 2& 4& 2\\ 4& 1& 1\end{array}\right)& =1\cdot \left|\begin{array}{cc}4& 2\\ 1& 1\end{array}\right|-2\cdot \left|\begin{array}{cc}2& 2\\ 4& 1\end{array}\right|+4\cdot \left|\begin{array}{cc}2& 4\\ 4& 1\end{array}\right|\\ & =1(4-2)-2(2-8)+4(2-16)\\ & =2-2(-6)+4(-14)\\ & =2+12-56\\ & =-42\ne 0\end{array}$$

495 Let $x_1,x_2,x_3$ be vectors in a vector space. Then these vectors are linearly independent if and only if the vectors $x_1+x_2$, $x_2+x_3$, and $x_3$ are linearly independent.

Solution

"$\Rightarrow$" First, let’s assume $x_1,x_2,x_3$ are linearly independent.
Suppose $\alpha (x_1+x_2)+\beta (x_2+x_3)+\gamma x_3=0$ for some scalars $\alpha ,\beta ,\gamma$.

$$\begin{array}{rl}& \alpha (x_1+x_2)+\beta (x_2+x_3)+\gamma x_3=0\\ & \alpha x_1+(\alpha +\beta )x_2+(\beta +\gamma )x_3=0\end{array}$$

Since $x_1,x_2,x_3$ are linearly independent, we must have:

$$\begin{array}{rl}\alpha & =0\\ \alpha +\beta & =0\\ \beta +\gamma & =0\end{array}$$

From this system: $\alpha =0$ implies $\beta =0$ which implies $\gamma =0$.
Therefore, $x_1+x_2$, $x_2+x_3$, $x_3$ are linearly independent.

"$\Leftarrow$" Now assume $x_1+x_2$, $x_2+x_3$, $x_3$ are linearly independent.
Let $\alpha x_1+\beta x_2+\gamma x_3=0$ for some scalars $\alpha ,\beta ,\gamma$.
We can express $x_1$ in terms of the given linearly independent vectors:

$$x_1=(x_1+x_2)-(x_2+x_3)+x_3$$

Therefore:

$$\begin{array}{rl}\alpha x_1+\beta x_2+\gamma x_3& =\alpha ((x_1+x_2)-(x_2+x_3)+x_3)+\beta x_2+\gamma x_3\\ & =\alpha (x_1+x_2)+(-\alpha )(x_2+x_3)+(\alpha +\beta )x_2+(\alpha +\gamma )x_3=0\end{array}$$

Since $x_1+x_2$, $x_2+x_3$, $x_3$ are linearly independent, we must have:

$$\begin{array}{rl}\alpha & =0\\ -\alpha & =0\\ \alpha +\beta & =0\\ \alpha +\gamma & =0\end{array}$$

This system implies $\alpha =\beta =\gamma =0$, showing that $x_1,x_2,x_3$ are linearly independent.

Ooor you simply show that the rank is 3.

$$\begin{array}{rl}\text{rank}\left(\begin{array}{c}{x}_1+x_2\\ x_2+x_3\\ x_3\end{array}\right)& =\text{rank}\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right)=3\end{array}$$

(subract row 3 from row 2, then row 2 from row 1)

553 Find the rank

Solution

Starting matrix:

$$A=\left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 2& 3& 4& 5& 6\\ 3& 4& 5& 6& 7\\ 4& 5& 6& 7& 8\end{array}\right)$$

Elimination steps:

$$\begin{array}{rl}& \stackrel{R_2-2R_1}{\to }\left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 0& -1& -2& -3& -4\\ 3& 4& 5& 6& 7\\ 4& 5& 6& 7& 8\end{array}\right)\\ & \stackrel{R_3-3R_1}{\to }\left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 0& -1& -2& -3& -4\\ 0& -2& -4& -6& -8\\ 4& 5& 6& 7& 8\end{array}\right)\\ & \stackrel{R_4-4R_1}{\to }\left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 0& -1& -2& -3& -4\\ 0& -2& -4& -6& -8\\ 0& -3& -6& -9& -12\end{array}\right)\\ & \stackrel{R_3-2R_2}{\to }\left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 0& -1& -2& -3& -4\\ 0& 0& 0& 0& 0\\ 0& -3& -6& -9& -12\end{array}\right)\\ & \stackrel{R_4-3R_2}{\to }\left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 0& -1& -2& -3& -4\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right)\end{array}$$

The matrix reduces to row echelon form with exactly two non-zero rows. Therefore, $\text{rank}(A)=2$.

Looking at the pattern, we can observe the matrix has a special structure where each row is an arithmetic sequence, and each row is obtained by adding a constant to the previous row. This explains why we get rank 2 - there are only two linearly independent patterns in the matrix: Increasing along rows by 1, increasing along columns by 2 → constant slope.

References

TU Wien

example format:

> [!EXAMPLE] Aufgabe 1
> 
>Man überprüfe die Gleichung
>$$
1^{2} + 2^{2}+3^{2}+\dots+n^{2} = \frac{n(n+1)(2n+1)}{6}
>$$
>für die ersten fünf natürlichen Zahlen und beweise sodann deren Gültigkeit für alle natürlichen Zahlen durch vollständige Induktion.

Your task is to OCR the next exercises statements like this too!
All the ones you can see, in separate callouts.
No code interpreter.
Return in backticks.
Follow the latex format of using `$` for inline math and `$$` for block math.