boolean algebra

See also logic.

Boolean lattice or boolean algebra

A boolean lattice is a lattice which has a greatest element $\top$ and a least element $\perp$, and complementation for every element: $a\wedge a^{\prime }=\perp$ and $a\vee a^{\prime }=\top$.
2 neutrale elemente (eines bezüglich infimum und eines bezüglich supremum)

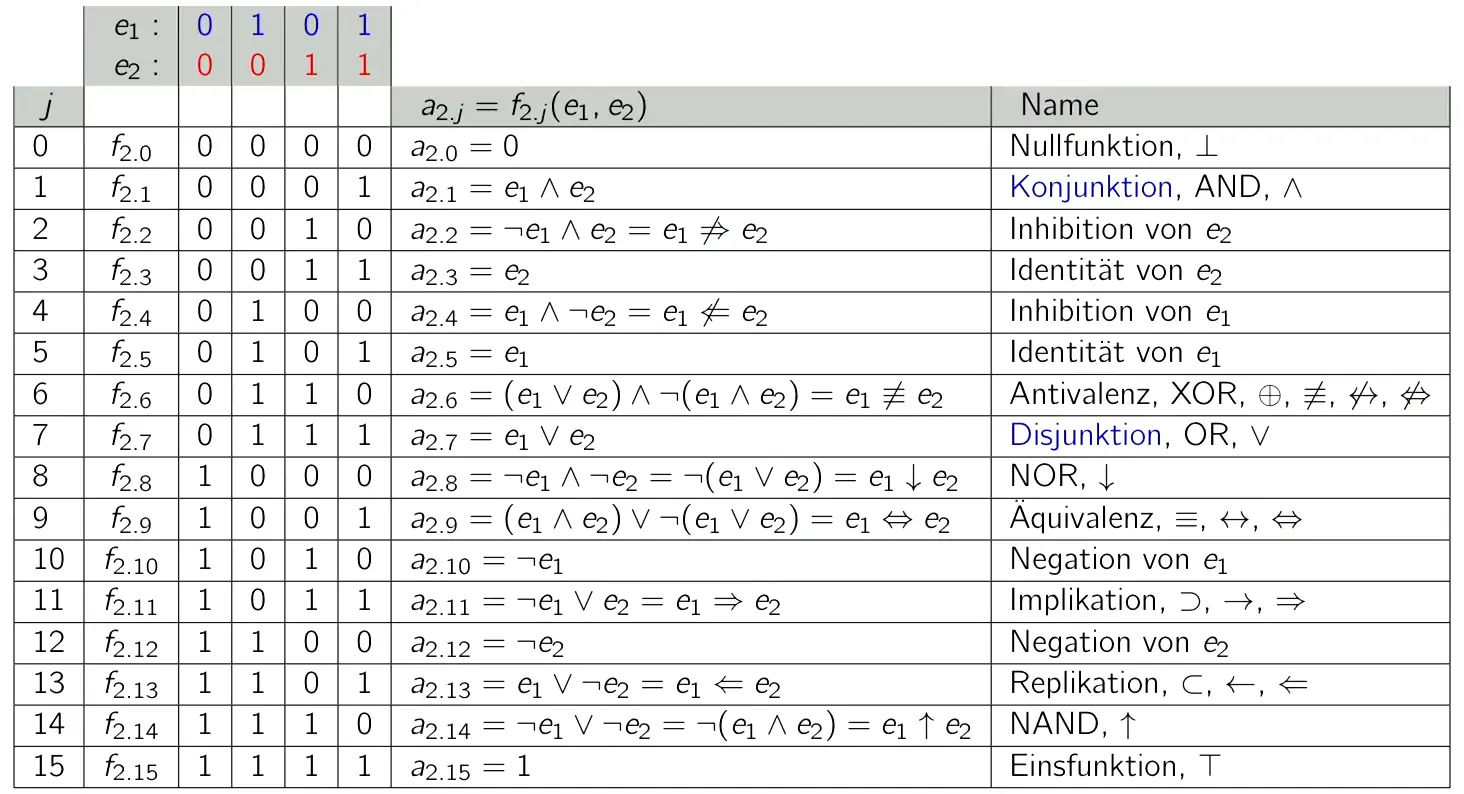
All possible functions for two inputs and a single output:

The column headers are the values of $e_i$, the values are $f_{1,j}(e_i)$.
For 2 variables, 1 output:

NNF (negation normal form): Negations only in front of variables.
Literal: Variable or its negation.
CNF (conjunctive normal form): AND of ORs of literals $(e_0\wedge \cdots \wedge e_n)\vee \cdots \vee (e_m\wedge \cdots \wedge e_p)$.
DNF (disjunctive normal form): OR of ANDs of literals $(e_0\vee \cdots \vee e_n)\wedge \cdots \wedge (e_m\vee \cdots \vee e_p)$.

$\neg a\wedge b\wedge c⟺(\neg a\wedge b\wedge c)\vee 0⟺(\neg a\wedge b\wedge c)\wedge 1$

→ It’s DNF & CNF (it always is both if there is just a single operation).

CCNF (canonical CNF): OR of ANDs of literals, where each AND contains all variables.
CDNF (canonical DNF): AND of ORs of literals, where each OR contains all variables.
Maxterm: OR of all literals to make a 0 for a given input.
Minterm: AND of all literals to make a 1 for a given input.

EXAMPLE

Here we just choose max/minterm such that we have the least negations.

Why are they called max / minterm?

$0\wedge 1=\min \{0,1\}$
$0\vee 1=\max \{0,1\}$

Rearrange to CNF / DNF

(1) Replace any symbols by $\wedge ,\vee ,\neg$:
$G⟺H\to (G⟹H)\wedge (H⟹G)$
$G=H\to (\neg G\vee H)$
…
(2) Iterate the following until no more changes:
$\neg \neg G\to G$
$\neg (G\wedge H)\to (\neg G\vee \neg H)$ (De Morgan)
$\neg (G\vee H)\to (\neg G\wedge \neg H)$ (De Morgan)
(3) Iterate the following until no more changes:
$(G\vee (H\wedge I));((H\wedge I)\vee G)\to ((G\vee H)\wedge (G\vee I))$ (Distributive)

If then else (ITE) notation

$\text{ITE}(a,b,c)$ → if (a == true) then b else c
e.g. boolean operators:
$a\equiv \text{ITE}(a,1,0)$
$a\wedge b\equiv \text{ITE}(a,b,0)$
$a\vee b\equiv \text{ITE}(a,1,b)$
$\neg a\equiv \text{ITE}(a,0,1)$
$a⟹b\equiv \text{ITE}(a,b,1)$

Shannon decomposition

Let $f:\{0,1{\}}^n\to \{0,1\}$ (function with $n$ inputs and a boolean output: $f(x_1,\dots ,x_n)$)
The cofactor $f_{x_i,1}$ of $f$ on $x_i$ is where $x_i$ is set to $1$:
$f_{x_i,1}(x_1,\dots ,x_n)=f(x_1,\dots ,x_i=1,\dots ,x_n)$
The cofactor of $f_{x_i,0}$ of $f$ on $x_i$ is where $x_i$ is set to $0$:
$f_{x_i,0}(x_1,\dots ,x_n)=f(x_1,\dots ,x_i=0,\dots ,x_n)$
The shannon decomposition is then:

$$f=(x_i\wedge f_{x_i,1})\vee (\neg x_i\wedge f_{x_i,0})$$

Which can also be written as: $\text{ITE}(x_i,f_{x_i,1},f_{x_i,0})$
This can be useful for simplifying boolean expressions, since you can pick any particular $x_i$, set it to $0$, $1$, and then only have to look at the corresponding cofactors which might be far simpler.

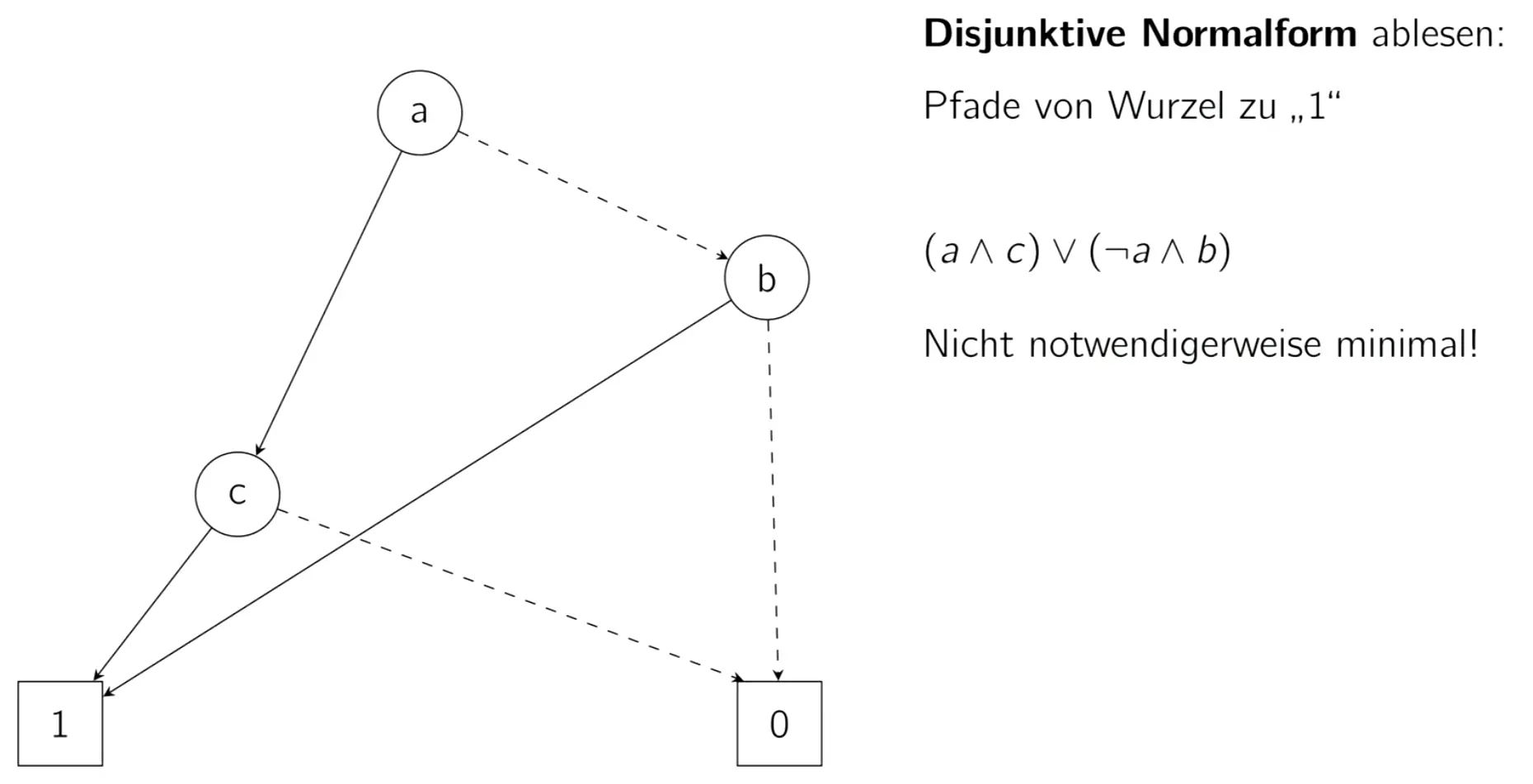
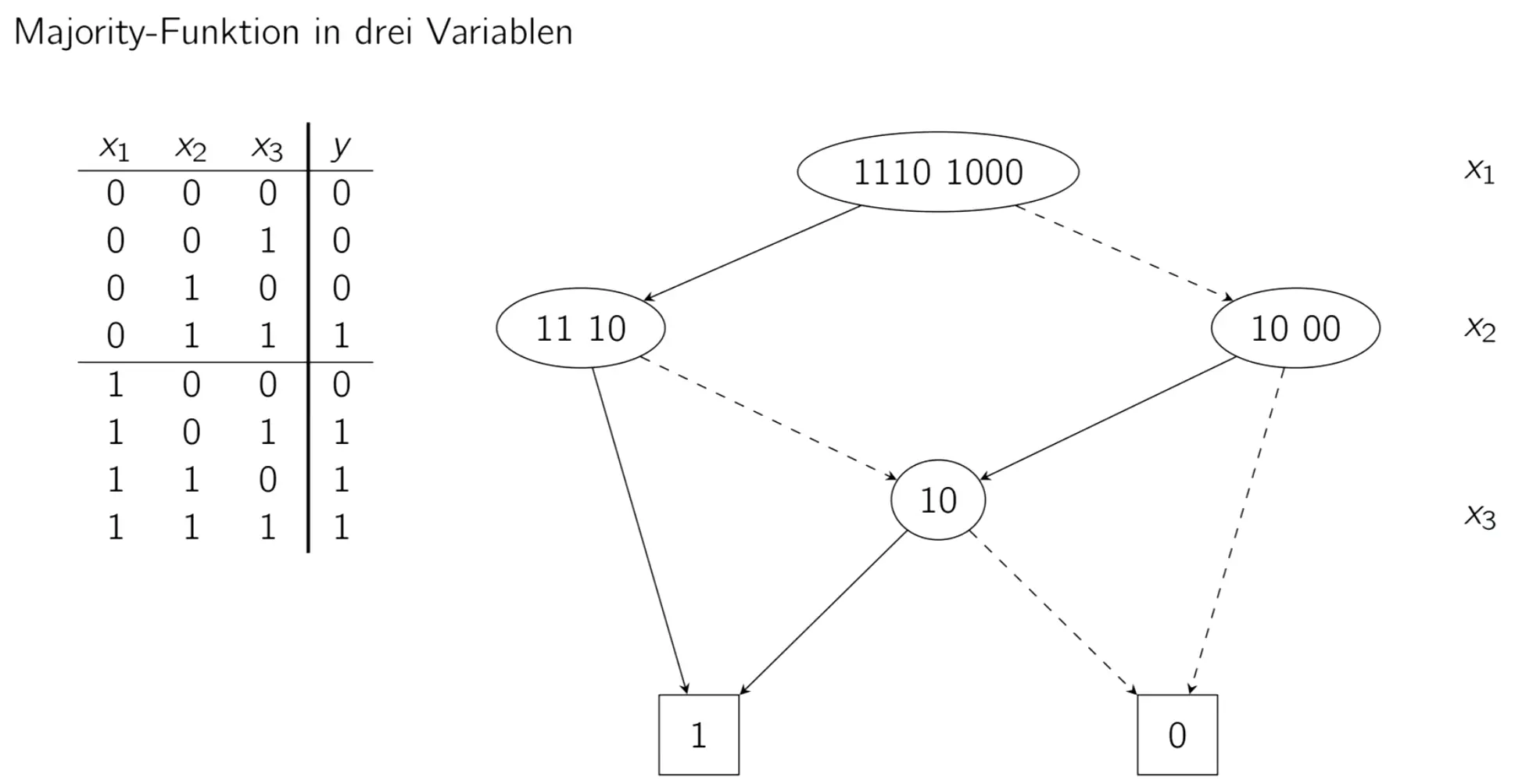
Binary decision diagrams (BDDs)

A BDD is a directed acyclic graph where each node represents a boolean variable, and the edges represent the value of that variable. The terminal nodes are the output values. The graph is reduced by merging nodes that have the same children and by removing nodes whose edges all point to the same child.
The DNF is then the set of paths from the root to the terminal nodes that evaluate to 1. The CNF is the set of paths that evaluate to 0, with the truth values negated (to preserve the end result of the equation).

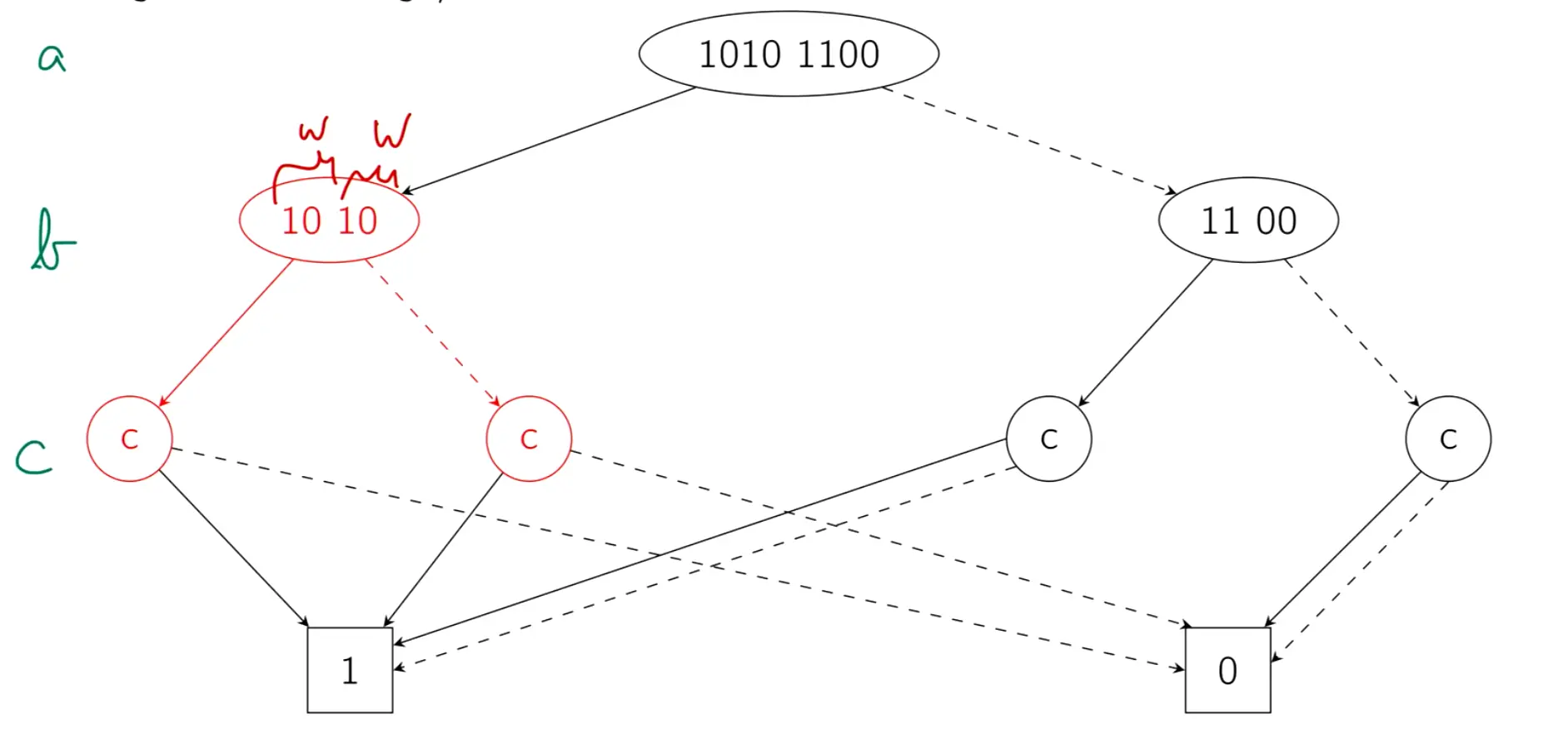
Beads

A bead is the truth values lined up from bottom to top. For $a\wedge b$ this would be $1000$, the first block corresponds to the first variable being true, the second one to it being false (like shannon decomposition).
If we have the same values on the left as on the right side it’s called a square, e.g. $10011001$.
Beads have the form of $ww$, with $w$ being a word of length $2^{n-1}$.
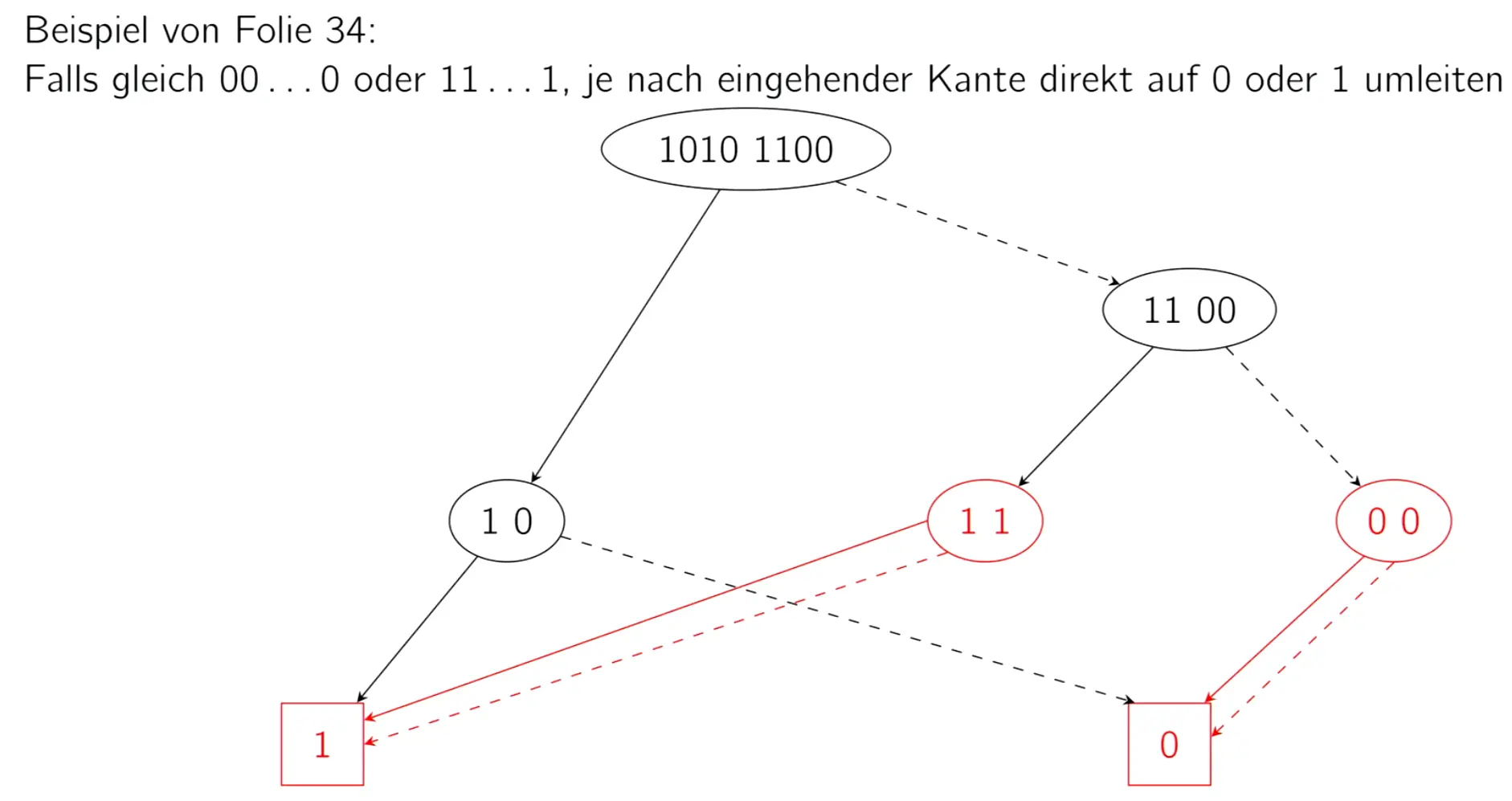
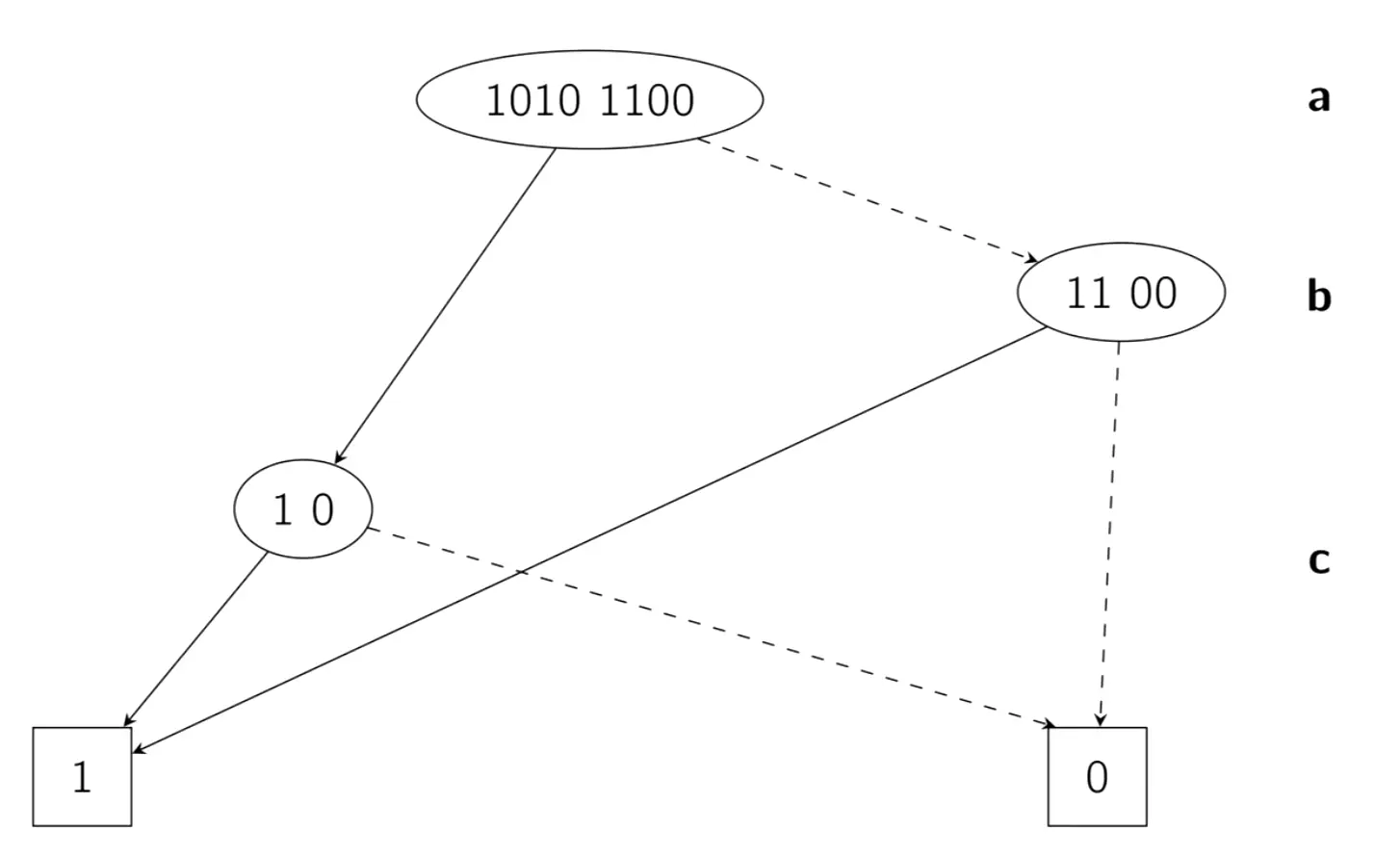
If the two words are the same in the tree, we can merge. If they contain only 1s or only 0s, we collapse it to pointing to only 1 or 0.


The values of the nodes are the function results (not the variable values). Edges are based on the function formula.
The order of variables makes a big difference in this method.
What’s nice is that you can easily chain the beads.

The majority function ( $\ge$ half true) is quite simple as a BDD