first order optimization

First Order optimization

Optimization methods that only use gradient information (first derivatives) $\nabla f(x)$ to update parameters. The gradient points in the direction of steepest ascent, so we move in the opposite direction to minimize the function:

$$x_{t+1}=x_t-{\alpha }_t\nabla f(x_t)$$

where $\alpha$ is the learning rate at iteration t.
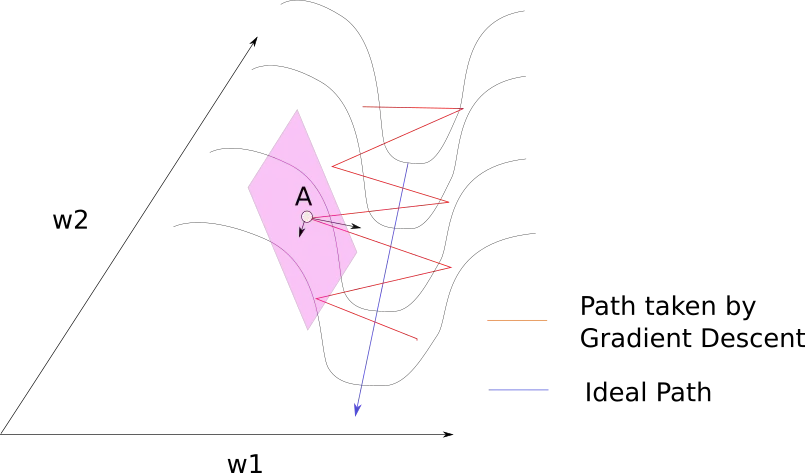
Limitations: Cannot account for interactions between parameters or local curvature of the loss surface. May oscillate in narrow valleys or move slowly across plateau regions.

Linear approximation

First order methods effectively construct a linear approximation of the function at each point:

$$f(x+\Delta x)\approx f(x)+\nabla f(x{)}^T\Delta x$$

This approximation becomes less accurate as we move away from the current point, explaining why small step sizes are often necessary.

Key characteristics

First order methods are computationally efficient per iteration, requiring only $O(n)$ computations for $n$ parameters. However, they can struggle with ill-conditioned problems where the objective function varies at dramatically different scales in different directions.

Example

gradient descent: The simplest first order method, directly follows the negative gradient, using fixed step size. Can be sensitive to the choice of learning rate and scaling of different parameters.
Adam: Combines momentum and adaptive learning rates, making it more robust to different scales and easier to tune. Maintains running estimates of first moment (mean) and second moment (uncentered variance) of gradients.

Limitations

First order methods can struggle with ill-conditioned problems where the gradient poorly indicates the true direction to the minimum. They may zigzag in narrow valleys or move slowly across plateaus where gradients are small but consistent.