k-means

k-means

An unsupervised learning algorithm that partitions $n$ data points into $k$ clusters by iteratively assigning points to the nearest cluster center and updating centers as the mean of assigned points.

Given data $\{{\mathbf{x}}_i{\}}_{i=1}^n$ and number of clusters $k$, it minimizes:

$$J=\sum _{i=1}^n\sum _{j=1}^k{r}_{ij}\Vert {\mathbf{x}}_i-{\mathbf{\mu }}_j{\Vert }^2$$

where $r_{ij}=1$ if point $i$ belongs to cluster $j$ (else 0), and ${\mathbf{\mu }}_j$ is the centroid of cluster $j$.

First we initialize $k$ centroids ${\mathbf{\mu }}_1,...,{\mathbf{\mu }}_k$ (often randomly from data points)
The algorithm alternates between two steps until convergence:

1. Assignment: Assign each point to the nearest centroid: for each point ${\mathbf{x}}_i$: assign to cluster $c_i=\arg {\min }_j\Vert {\mathbf{x}}_i-{\mathbf{\mu }}_j{\Vert }^2$
2. Update: Recompute centroids as the mean of assigned points: for each cluster $j$: update ${\mathbf{\mu }}_j=\frac{1}{|S_j|}{\sum }_{i\in S_j}{\mathbf{x}}_i$

where $S_j=\{i:c_i=j\}$ is the set of points assigned to cluster $j$.

This simple procedure guarantees that the objective $J$ decreases monotonically, though it only finds local minima.
The final clustering depends heavily on initialization - poor starting centroids can lead to suboptimal solutions.

Practical considerations / Properties & limitations

Choosing $k$: Often determined by domain knowledge or methods like the elbow method (plot reconstruction error vs $k$) or silhouette analysis.

Initialization: k-means++ improves on random initialization by choosing centroids that are far apart, leading to better convergence and final clusters.

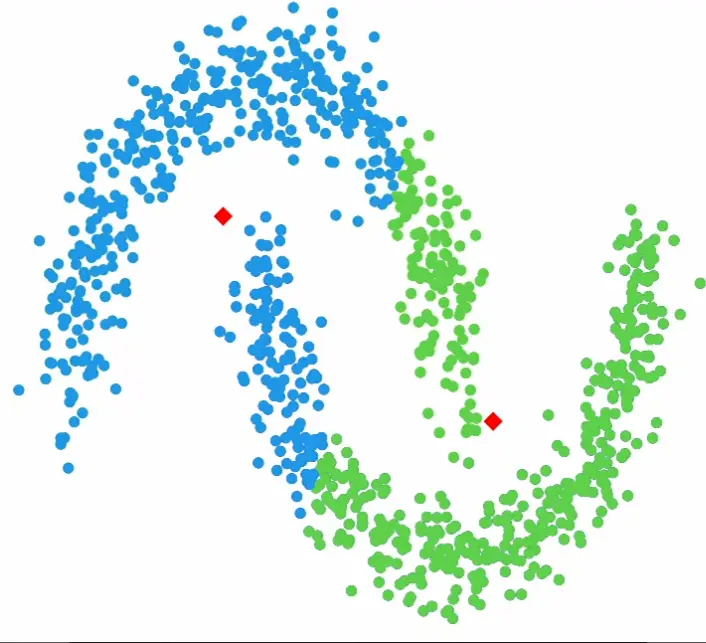
Assumptions: k-means implicitly assumes spherical clusters of similar size. It struggles with elongated or overlapping clusters, where algorithms like gaussian mixture models or DBSCAN may perform better.
K-means focuses on minimizing variance within clusters (“compactness” within clusters) but does not explicitly maximize separation between clusters.

Sensitive to noise an outliers: Outliers can skew centroids significantly. Preprocessing steps like outlier removal or using k-medoids can help.

The algorithm’s $O(nkd)$ complexity per iteration (for $d$-dimensional data) makes it efficient for large datasets. Variants include mini-batch k-means for even larger data and kernel k-means for non-linearly separable clusters.

Example data it struggles with: