state space model

https://goombalab.github.io/blog/2025/tradeoffs/

State space models are good for tasks that do not require (long) history(time)-dependence.

This is because you can process the entire series $x_t$ with a parallelizable scan by making the processing of each element of the sequence independent of others, i.e. there is no shared state between the elements of the sequence, as opposed to RNNs or LSTMs.
An example task would be character-level language modelling.
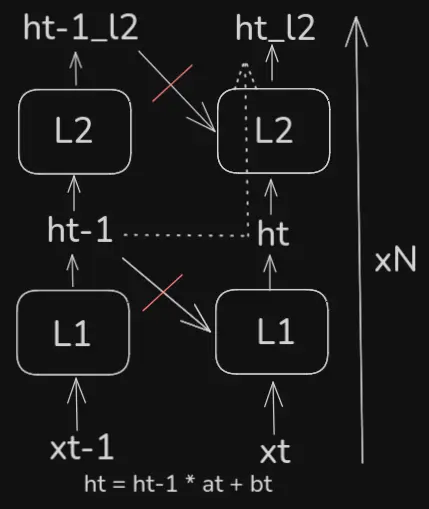
If such dependence is necessary, one can stack layers of SSMs, where the hidden state of each layer still can’t have any knowledge of the previous hidden states of the same layer, but can have knowledge of the hidden states of the previous layer - then layers have to be processed sequentially, but the sequence elements (which are usually much more) can still be processed in parallel. This way, information about the past is implicitly passed via the hidden state, which is computed as $h_t^L=h_{t-1}^L\cdot a_t+b_t$, where $a_t,b_t$ are the weights and biases of the layer $L$ at time $t$.
This is akin to convolutions, which have a limited, local receptive field, but which gets implicitly expanded by stacking layers (also similar to the segment-level recurrence of transformer-xl).

SSMs

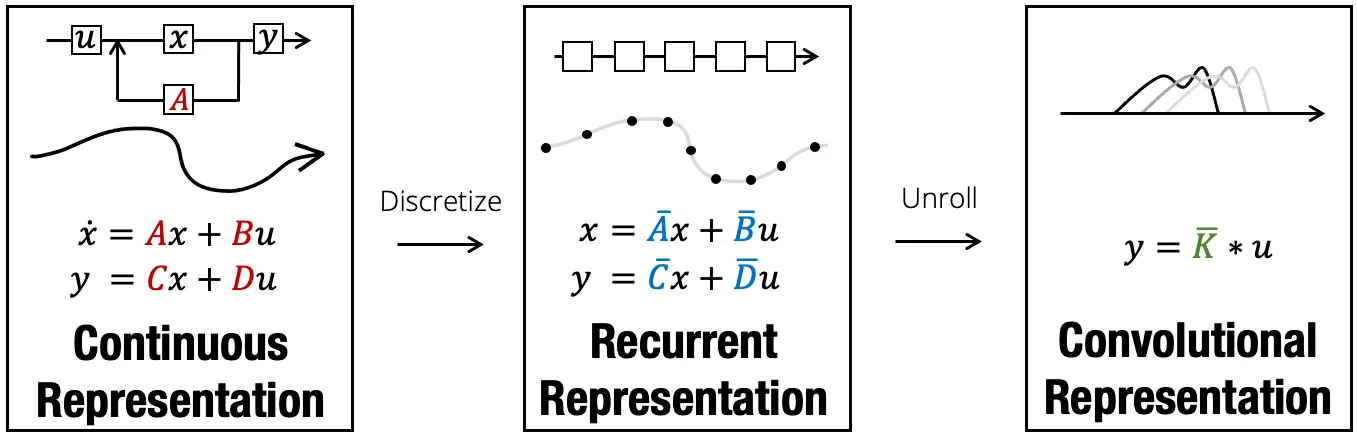
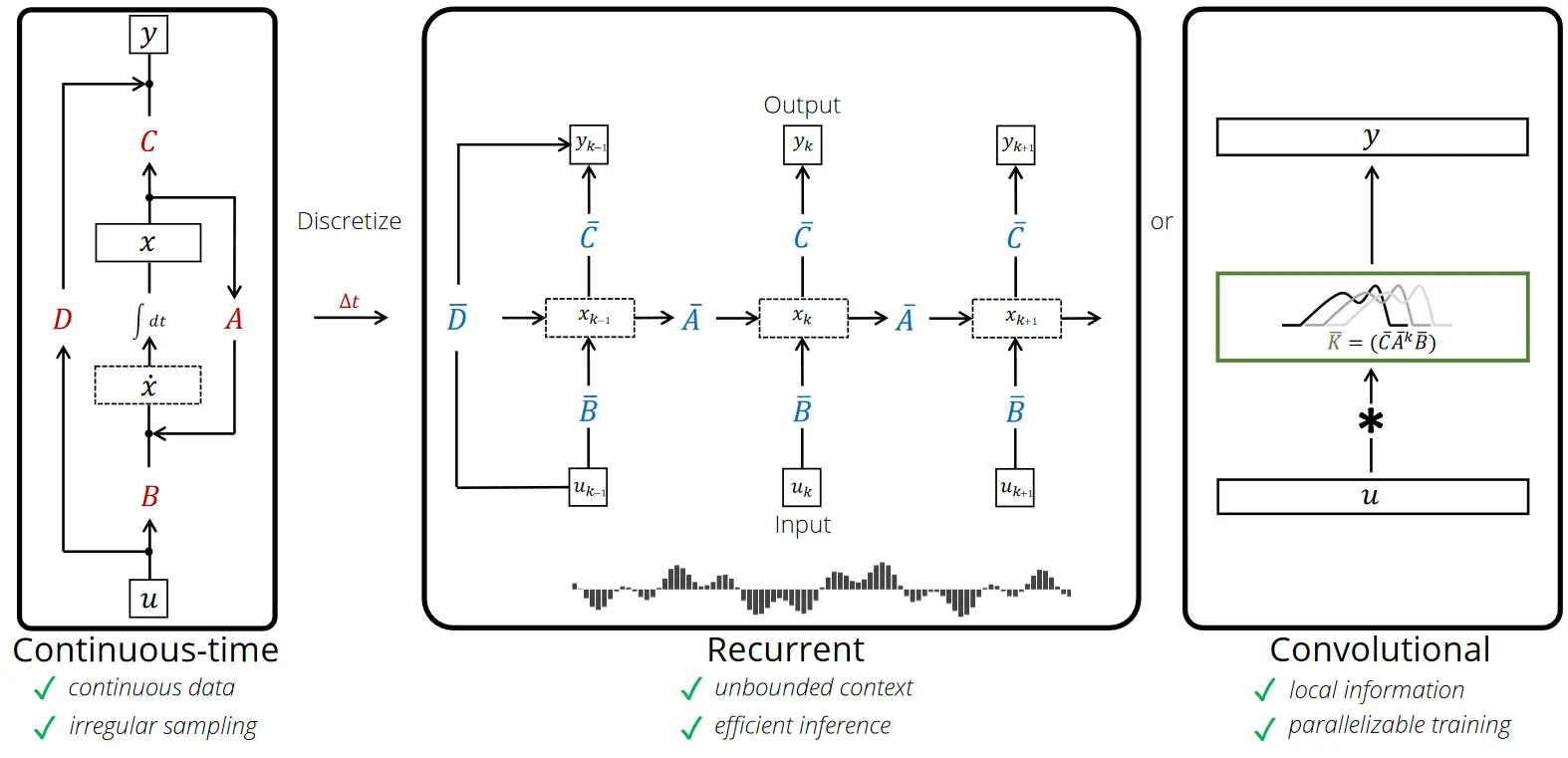
Many SSMs fall under the following framework:
Given a length $L$ sequence of inputs ${\mathbf{x}}_{1:L}\in {\mathbb{R}}^{L\times D}$, a general class of linear recurrences with hidden states ${\mathbf{h}}_{1:L}\in {\mathbb{R}}^{L\times N}$ and outputs ${\mathbf{y}}_{1:L}\in {\mathbb{R}}^{L\times D}$ can be computed as shown:

$$\begin{array}{r}{\mathbf{h}}_k={\mathbf{A}}_k{\mathbf{h}}_{k-1}+{\mathbf{B}}_k{\mathbf{x}}_k\\ {\mathbf{y}}_k=g({\mathbf{h}}_k,{\mathbf{x}}_k)\end{array}$$

where ${\mathbf{A}}_k\in {\mathbb{R}}^{N\times N}$ is the state transition matrix, ${\mathbf{B}}_k$\boldsymbol{B}{k} \in \mathbb{R}^{N\times D}$istheinputmatrix,and$g(\cdot)$istheoutputfunction.[[time-invariance|Timeinvariant]]SSMshavestaticdynamicsparamtersacrosstime,i.e.$\boldsymbol{A}{k} = \boldsymbol{A}$and$\boldsymbol{B}_{k} = \boldsymbol{B} \quad \forall k$ (for example S4 (SSM))

References

https://huggingface.co/blog/lbourdois/get-on-the-ssm-train
Birdie - Advancing State Space Modelswith Reward-Driven Objectives and Curricula