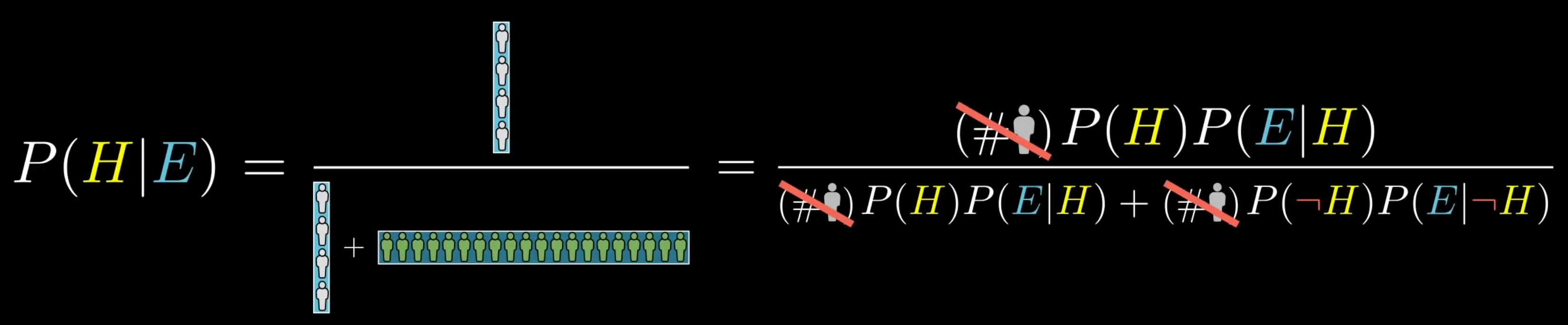
Bayes Theorem

Baye’s Theorem: What’s $P(H\mid E)$?

$$\begin{array}{r}\underset{\begin{array}{c}\text{posterior}\\ \text{updated beliefs}\end{array}}{\underbrace{P(H\mid E)}}=\frac{\stackrel{\begin{array}{c}\text{update/likelihood}\\ \text{how well new }\\ \text{observations fit}\\ \text{previous beliefs}\end{array}}{\overbrace{P(E\mid H)}}\stackrel{\begin{array}{c}\text{prior}\\ \text{previous beliefs}\end{array}}{\overbrace{P(H)}}}{\underset{\begin{array}{c}\text{evidence}\\ \text{normalization term}\end{array}}{\underbrace{P(E)}}}\end{array}$$

What are the chances of me having cancer? If I don’t know anything else, the chances are the same as anyone else in my demographic → That’s the prior $P(H)$, the best guess without any further info.
If I take a test or have a symptom, I get extra information about $H$ and can update that information.
$P(E\mid H)$ is something we can usually calculate pretty easily as opposed to updating $P(H|E)$ (would need to collect more data, …).

The basic idea of bayesian statistics is sequentially updating your beliefs given new information.

New evidence should not determine beliefs in a vacuum.

Visual explanation

Interactive visualization: https://srulix.com/projects/bayesground?standalone=true

$H$ … hypothesis “is a librarian” vs. “is a farmer” $\neg H$
$E$ … evidence “is shy”
$P(H)$ … how likely is it that somebody is a librarian (prior; If we have no clue, it could be a guess, or uniform distribution 50/50 in this case).
$P(H|E)$ … how likely is it that somebody is a librarian, given that they are shy (posterior we’d like to know).
$P(E|H)$ … how likely is it that a librarian is shy.
$P(\neg H)$ … how likely is it that somebody is a farmer.
$P(E)$ … how likely is it that somebody is shy (out of all librarians and farmers).
$P(E|\neg H)$ … how likely is it that a farmer is shy.

$P(H)$. Questions about the personalities and sterotypes shift around the relevant likelihoods $P(E|H)$ and $P(E|\neg H)$.

Questions about the context shift around the prior

Among cases where the evidence is true, how often is the hypothesis true?

The probability and the hypothesis being true form an area, see below.

$P(E|H)\cdot P(H)=P(H\cap E)$

The numerator in Baye’s rule is the probability of both the hypothesis and evidence occuring (chain rule of probability). ¹

Spam filter

$$P(\text{spam}|\text{word})=\frac{P(\text{word}|\text{spam})P(\text{spam})}{P(\text{word})}$$

$P(\text{spam})$ … how likely is it that an email is spam (prior)
$P(\text{word}|\text{spam})$ … how likely is it that the word appears in spam emails (likelihood)
$P(\text{word})$ … how likely is it that the word appears in any email (evidence, aka marginal likelihood)
$P(\text{spam}|\text{word})$ … how likely is it that an email is spam, given that it contains the word (posterior)

Sensitivity and specificity

Assume a drug test which has 90% sensitivity (true positive rate or “recall”), i.e. the probability of a positive result given it’s a drug user $P(+\mid \text{user})=0.9$.
And 80% specificity (true negative rate or “selectivity”), i.e. $P(-\mid \text{non-user})=0.8$.

This test is quite bad, 20% of non-users get a false positive. Let’s also say 10% of the population use the drug $P(H)=0.1$.
The probability of someone being a drug-user after testing positive is:

$$\begin{array}{rl}P(\text{user}\mid +)& =\frac{P(+\mid \text{user})P(\text{user})}{P(+\mid \text{user})P(\text{user})+P(+\mid \text{non-user})P(\text{non-user})}=\frac{0.9\cdot 0.1}{0.9\cdot 0.1+0.2\cdot 0.9}=\frac{1}{3}\end{array}$$

So the probability that you did actually use the drug is only 33%. Even if the sensitivity is 1, we only reach ~35%.
This error gets better for more common events.

This is also relevant for machine learning: We can get close to 100% accuracy just by ignoring very rare samples (high sensitivity, low specificity).

If we don’t know $P(E)$, we can express it as conditional probabilities we do know with the help of the law of total probability.

$$\begin{array}{r}P(H\mid E)=\frac{P(E\mid H)P(H)}{P(E\mid H)P(H)+P(E\mid H^c)P(H^c)}\end{array}$$

Or generally, for multiple hypotheses $\{H_i{\}}_{i=1}^n$ that partition the sample space$E$:

$$\begin{array}{r}P(H_i\mid E)=\frac{P(E\mid H_i)P(H_i)}{{\sum }_{j=1}^{n}P(E\cap H_j)}=\frac{P(E\mid H_i)P(H_i)}{{\sum }_{j=1}^{n}P(E\mid H_j)P(H_j)}\end{array}$$

So to get $P(E)$, we consider all the ways $E$ can happen, weighted by how likely each way is.
If we don’t have “all hypotheses”, we can add an “other” hypothesis $H_{n+1}$ with $P(H_{n+1})=1-{\sum }_{i=1}^{n}P(H_i)$.

The marginal likelihood normalizes the posterior

The marginal likelihood represents the total probability of observing our data, accounting for all possible parameter settings according to our prior beliefs. It serves as the normalizing constant in Bayes Theorem:

$$p_{\theta }(\mathbf{z}|\mathbf{x})=\frac{p_{\theta }(\mathbf{x}|\mathbf{z})p_{\theta }(\mathbf{z})}{p_{\theta }(\mathbf{x})}$$

Unlike the likelihood, which evaluates parameter settings individually, the marginal likelihood evaluates the model as a whole, integrating over the entire parameter space.

Link to original

A good understanding of bayes theorem implies that experimentation is essential.

If you only ever observe $A$, you become more and more certain that’s how the world works. Being very certain that $A$ is true / the only thing that works would lead to a self-fulfilling prophecy.
→ change / explore

Bayesian Inference

Treats all parameters ¹ as random variables with a prior distribution $p(\theta )$.
Update via Bayes’ rule:

$$p(\theta \mid X)=\frac{p(X\mid \theta )p(\theta )}{p(X)}$$

The posterior $p(\theta \mid X)$ represents our updated beliefs about parameters after seeing data.

Computing it often requires intractable integrals (for the marginal likelihood $p(X)$), leading to approximation methods:

• Variational inference - approximate posterior with simpler distribution
• Markov chain Monte Carlo - sample from posterior distribution
• Laplace approximation - Gaussian approximation around posterior mode

Link to original

Visualization of how different priors and likelihoods affect the posterior.

Todo

Bayes' factor

References

probability
bayesian statistics

The Bayesian Trap

Footnotes

1. I find it much easier to reason over the rule / understand the visualization after knowing this identity… why don’t any of the popular explanations mention this? ↩