Brain Criticality - Optimizing Neural Computations - Artem Kirsanov

Brain Criticality - Optimizing Neural Computations

Key takeaways

• at critical temperature, self-organizing systems exhibit a fractal structure, structures of simmilar size appear at simmilar proportion at different scales (infinite in both directions), furthermore, computational power and information storage are maximized near a critical point.
  • there is no characteristic scale, the whole resembles some of its parts at any scale (self-similarity)
  • power law == scale-free
  • distributions in systems following a power law suggests that it is near a phase transition (close to tipping to super/subcritical)
  • excitation - inhibition factor shapes the firing dynamics in the brain. it follows a power law

Neuronal activity

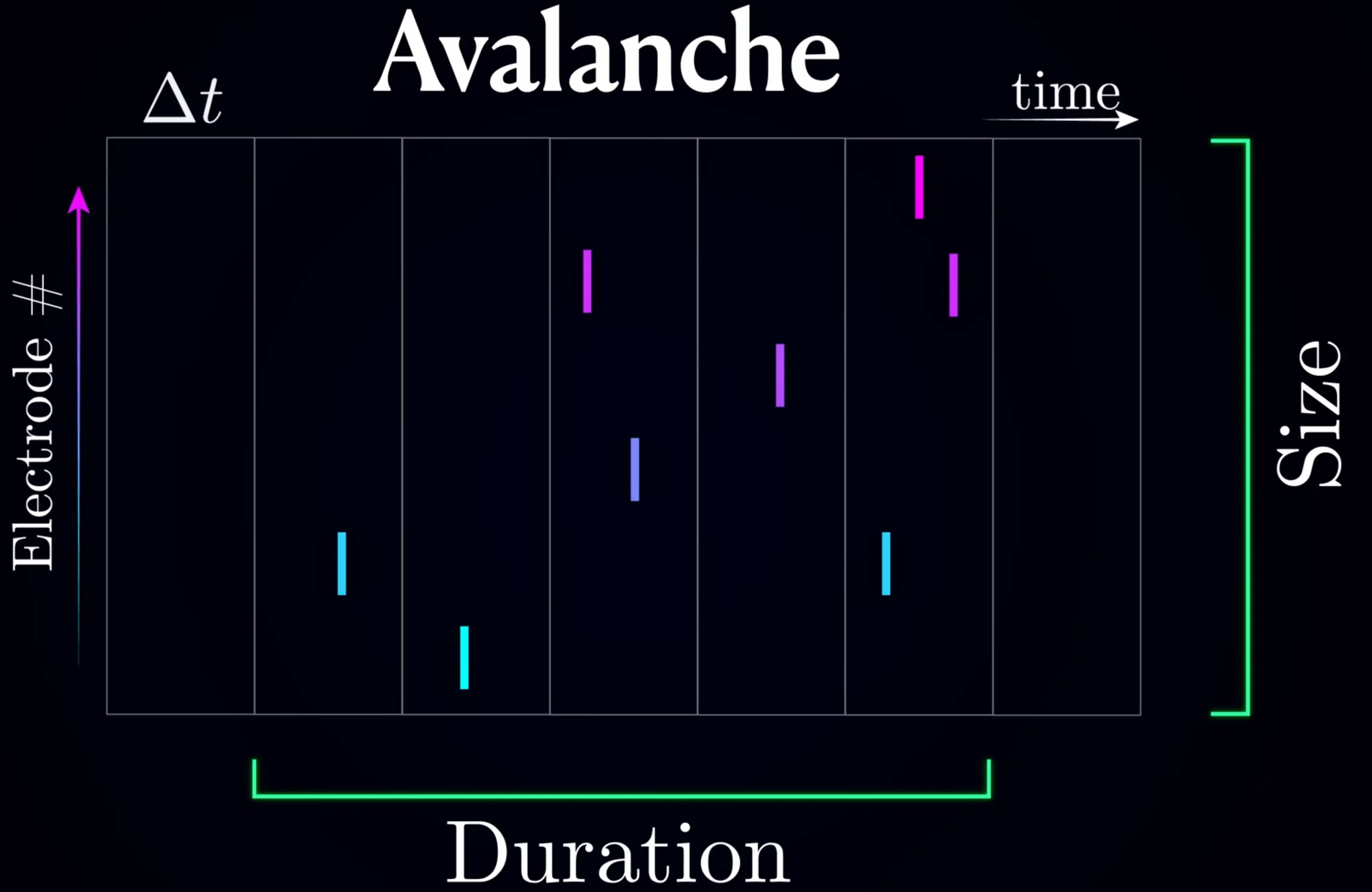
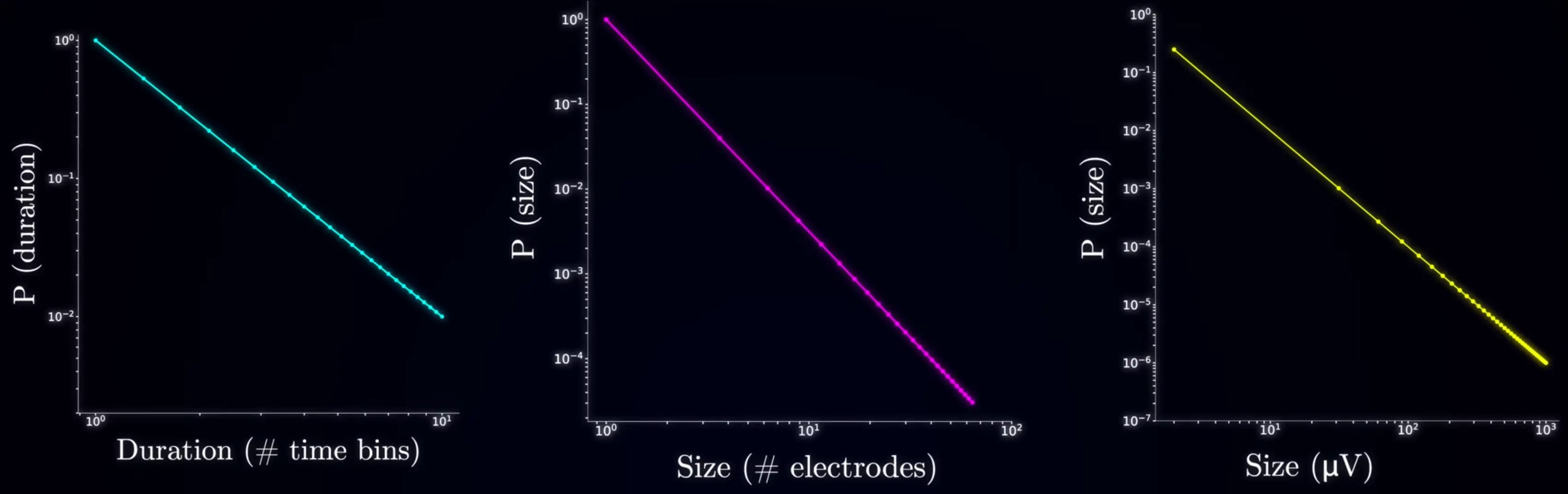
Neuronal activity can be seen as avalanches of signals, with a certain size and duration and amplitude.
These properties follow a power-law distribution, so the specific scale doesn’t mattter!

What is the ising model criticality analogue for the brain?

• temperature is the control parameter,
• magnetisation is the order parameter
  →
  In the brain / soup, criticality relates to the branching factor of excitation patterns.

TODO

go over branching model again, in more detail. Is it basically spiking NN?

Branching factor $\sigma$ == how many neurons get excited from a neuron firing.
The criticality point for this lies at $\sigma =1$, where signals are stably propagated, dying out eventually (?“due to stochasticity”?).
.5 → signal quickly dies out. 2→ signal get’s amplified to oblivion

! $\sigma$ is shaped by the balance between excitation and inhibition.

Just as with the sparsity-balance in engrams,

Suppressed inhibition → supercritical dynamics.
Supressed excitation → subcritical dynamics.

If there is too little firing, we can’t make inferences, if there is too much firing, we can’t make inferences. The critical point is the optimal point for information transmission (peak at $\sigma =1$, simmilar to dynamic correlation in the ising model).

TODO (not covered in this video) continue with The Cortex and The Critical Point - Understanding The Power of Emergence

“Universality classes”
$\frac{\alpha -1}{\tau -1}=\gamma$
“Quasicriticality”
Homeostasis of critical point

Neurons can also fire randomly, even if it is not in an immediate response to an input btw.

---

artem kirsanov