power law

The ratio of a specific kind of clusters / pattern is the same at any scale:

$$\frac{f(kx)}{f(x)}=g(k)$$

(the distribution of cluster-size does not dedpend on scale $x$)

The only (1-variable) function, for which this equation holds is the power law:

$$f(x)=A{x}^{-\gamma }$$ $$g(k)=\frac{f(kx)}{f(x)}=\frac{\cancel{A}{k}^{-\gamma }\cancel{x^{-y}}}{\cancel{A}\cancel{x^{-\gamma }}}=k^{-\gamma }$$

In log-log plots, power laws are straight lines.

A defining feature: Rare / Extreme events aren’t vanishingly unlikely

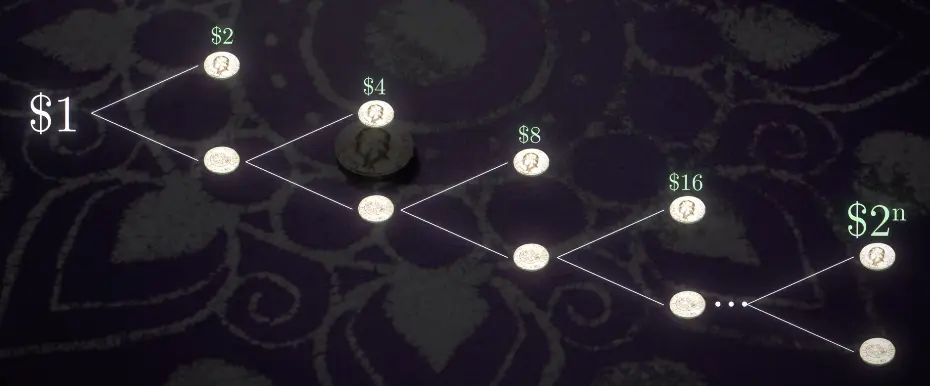
St. Petersburg Paradox

You flip a coin. The pot starts at $1.
Every time you get Heads, the pot doubles ($2,4,8\dots$).
The game ends on the first Tails.

Value $x=2k$: The payout grows as $2k$, where $k$ is the number of heads.

Probability $p=(1/2{)}^k$: The chance of reaching turn $k$ shrinks as $(1/2{)}^k$.

When you combine these, the exponentials cancel out, leading to infinite expected value:

$$\mathbb{E}[X]=\sum _{k=1}^{\infty }{2}^k\cdot {\left(\frac{1}{2}\right)}^k=\sum _{k=1}^{\infty }1=\infty$$

And the probability of getting a payout of exactly $x$ is:

$$P(X=x)\propto {\left(\frac{1}{2}\right)}^{{\log }_{2}x}=2^{-{\log }_{2}x}=\frac{1}{2^{{\log }_{2}x}}=\frac{1}{x}$$

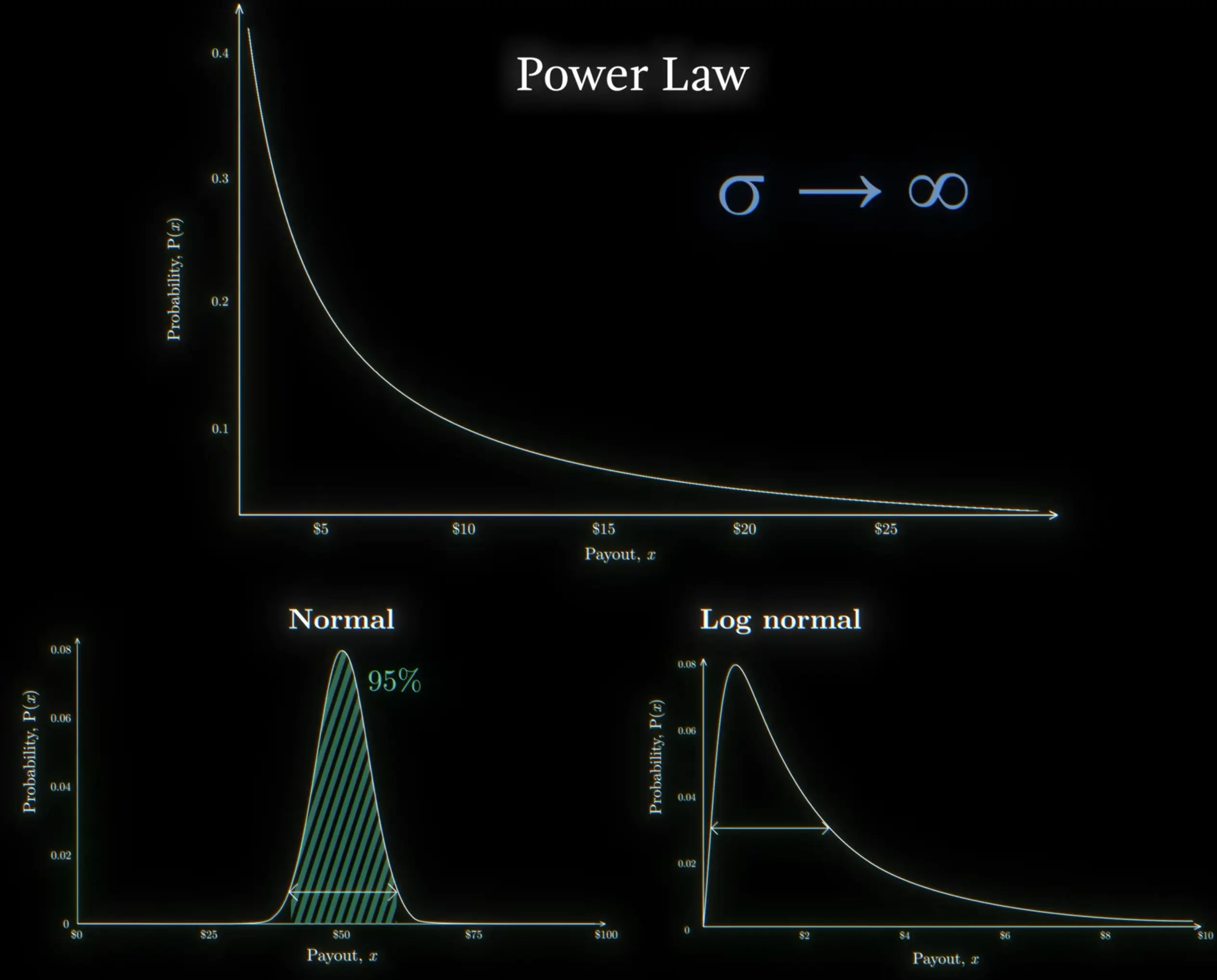
A payout of $x$ has probability proportional to $\frac{1}{x}$, so a 1mio dollar payout is unlikely but not vanishingly so.

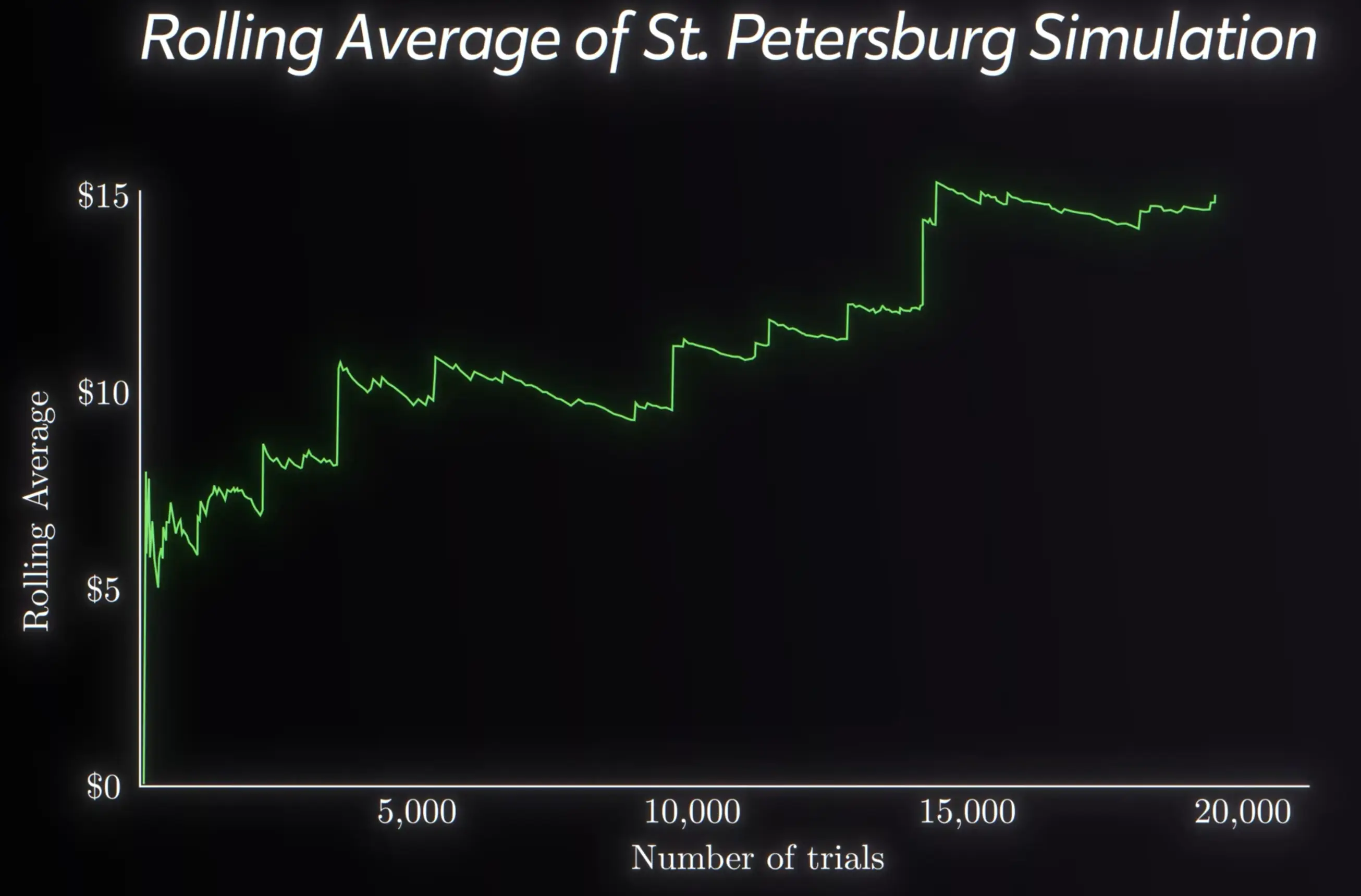
The tail is so heavy that if you keep measuring, occasionally you are going to measure extreme outliers which will skew the average significantly, making it diverge to infinity.

Whether a power law has infinite mean (or variance) depends on the exponent $\gamma$

If $\gamma \le 2$, the mean diverges to infinity. The tail is fat enough that the the longer you observe the system, the larger the average becomes.
If $2<\gamma \le 3$, it has finite mean but infinite variance, i.e. you can compute an average value, but the volatility is high / unpredictable (earthquakes, stocks, …).
If $\gamma >2$, the probability of rare events drops fast enough that the mean converges to a finite value. Behavior is more “normal”.