Density-Based Spatial Clustering of Applications with Noise (DBSCAN)
An unsupervised learning algorithm that identifies clusters as dense regions in feature space separated by low-density regions.
Unlike k-means, which requires specifying the number of clusters upfront, assumes spherical clusters and focuses on distances to centroids, DBSCAN discovers clusters of arbitrary shape by examining local point density.
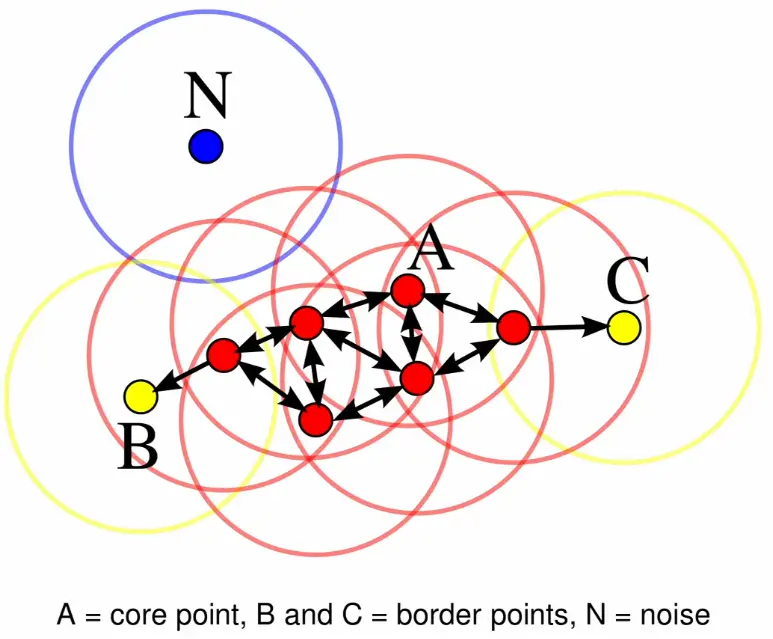
It has two hyperparameters: the radius defining a neighborhood, and , the minimum number of points required to form a dense region.DBSCAN classifies each point into one of three categories based on its local density:
Core points have at least neighbors within distance (including themselves). These form the backbone of clusters.
Border points are within of one or more core points but don’t have enough neighbors to be core points themselves. They belong to clusters but lie at their edges.
Noise points are neither core nor border - they lie in sparse regions and are considered outliers.
The algorithm builds clusters by connecting core points: if two core points are within of each other, they belong to the same cluster. Border points are then assigned to clusters based on their proximity to core points.
Practical considerations
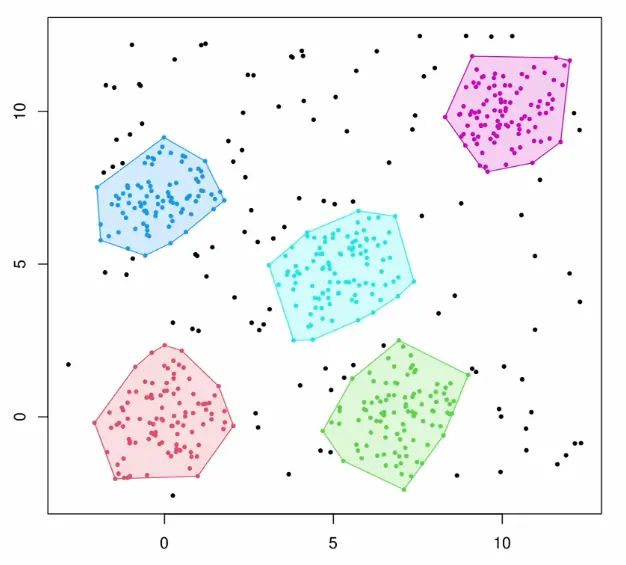
Discovering cluster count: DBSCAN automatically determines the number of clusters from the data rather than requiring it as input. This is a significant advantage over k-means when the number of natural groupings is unknown.
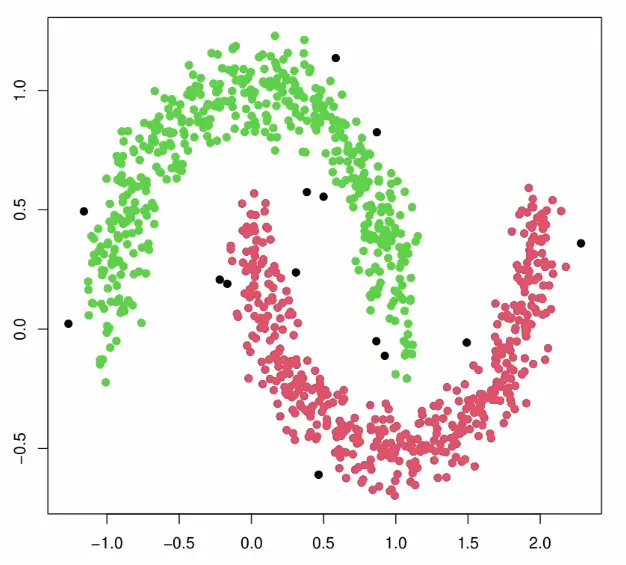
Arbitrary shapes: The density-based approach handles non-spherical, elongated, or irregularly shaped clusters that would confuse k-means’ distance-to-centroid criterion:
Noise robustness: Outliers are explicitly labeled as noise rather than forced into clusters, making DBSCAN more robust than k-means where every point must belong somewhere:
Parameter sensitivity: Performance depends heavily on choosing appropriate and . Too small fragments natural clusters; too large merges distinct ones. The k-distance graph (plotting distance to -th nearest neighbor) can help identify suitable values.
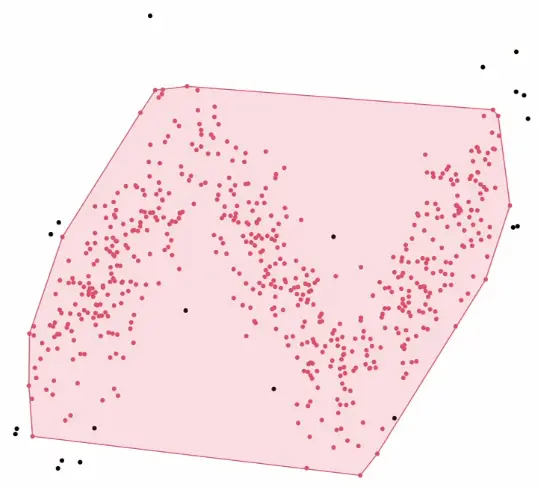
Varying density: DBSCAN struggles with clusters of substantially different densities - a single cannot capture both sparse and dense regions simultaneously. This is its primary limitation.
Variants like HDBSCAN address the varying density problem by building a hierarchy of clusters at multiple density thresholds.Failure mode - overlapping clusters with similar density get merged: