Growing Artificial Neural Networks for Control - the Role of Neuronal Diversity

year: 2024/05
paper: https://arxiv.org/pdf/2405.08510
website:
code: https://github.com/eleninisioti/GrowNeuralNets
connections: neuroevolution, developmental encoding, ITU Copenhagen, neuronal diversity, cell identity

---

Problem & motivation

Complex behavioral policies require non-homogenous networks, but NDPs are prone to collapsing to a substrate where all nodes have the same hidden state.
If all cells make the same local decisions, the network becomes homogeneous and cannot express complex control policies. The aim is to study a developmental approach that grows both topology and weights while keeping enough heterogeneity to avoid this collapse.

Takeaway

• Two simple mechanisms stabilize growth: immutable intrinsic lineage tags (identity that propagates on neurogenesis) and lateral inhibition (temporary neighbor suppression to avoid synchronized decisions).
• With these, a developmental process that grows topology and weights matches a single-shot indirect generator and is competitive with direct weight evolution on Brax RL tasks.
• Measured diversity (expected k-NN distance in hidden-state space) rises with inhibition and vanishes without tags.
• Indirect/developmental methods aren’t expected to beat direct on these tasks (little pressure for generalization/robustness). The contribution is making developmental control work/stable.

Networks & Training Setup

NDPs represent the system during growth as a directed graph whose nodes (cells) each carry a hidden state.

They split this hidden split into two parts: intrinsic (fixed, lineage tag) and extrinsic (mutable, environment-dependent).
At each growth step, every cell can (i) differentiate to update its extrinsic state using a shared DiffModel (GAT over the current graph), (ii) generate a new cell using a shared GenModel; the child inherits the parent’s intrinsic tag, and (iii) update an edge weight with a shared EdgeModel based on the states of the incident nodes.

The developmental process is seeded from $O+A$ cells, designated input/output units, each grown cell is a hidden unit.

After a fixed number of growth steps they read the grown graph as a recurrent neural network policy ¹ and evaluate it in an RL environment.

The three models are optimizes with DES (empirically found to perform better).
The number of trainable parameters (genotype) is independent of the final network size (phenotype).

Mechanisms to maintain diversity

1. Intrinsic lineage tags: initially unique one-hot vectors assigned to the seed cells and copied on neurogenesis.
2. lateral inhibition: whenever a cell differentiates, grows, or updates a connection, its neighbors are inhibited from doing the same action for a fixed window.

Experimental setup

Tasks: Brax/MuJoCo Reacher, Inverted Double Pendulum, HalfCheetah, Ant.
Growth horizon: 15 steps; inhibition window: 2 steps.
Extrinsic state: real vector (length 8).
Training: DES; results averaged over runs and evaluations.

Results

Baselines
Direct encoding: Evolve weights of a fixed-size RNN (100 neurons). ²
Single-shot indirect encoding: A hypernetwork-style³ generator (EdgeModel) that maps intrinsic tags to weights in one step, with a fixed architecture.

Results

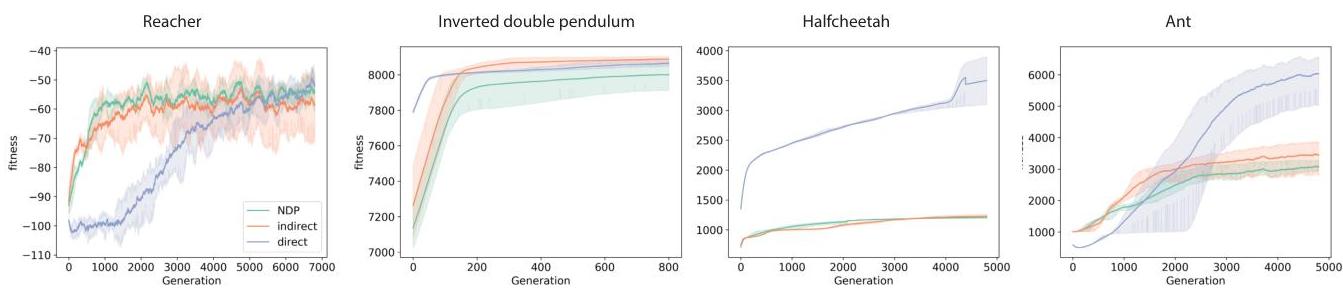
• With intrinsic tags (and helped by inhibition), NDP reaches performance comparable to the single-shot indirect baseline and competitive with direct encoding across the tasks.
• Without intrinsic tags, training collapses to trivial policies.
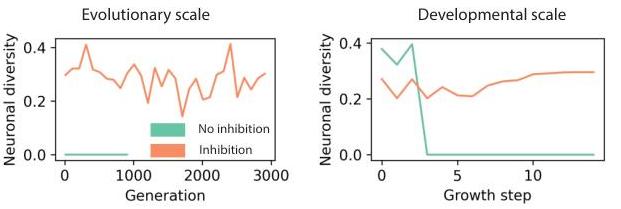
• Inhibition increases measured diversity both across evolutionary time (final networks per generation) and across developmental time (within a growth rollout).

How is diversity measured?

Let $h_i$ denote the hidden state vector of neuron $i$. For each neuron, compute the mean distance to its $k$ nearest neighbors ($k=10$) in hidden-state space, then average over neurons:

$$\text{diversity}=\frac{1}{N}\sum _i^N\left[\frac{1}{k}\sum _{j\in {\mathcal{N}}_k(i)}\mathrm{dist}\right(h_i,h_j\left)\right].$$

For the inhibition analysis, the intrinsic component is removed from $h_i$ so the metric reflects only learned extrinsic differences.

In orange is this paper’s version of NDP:

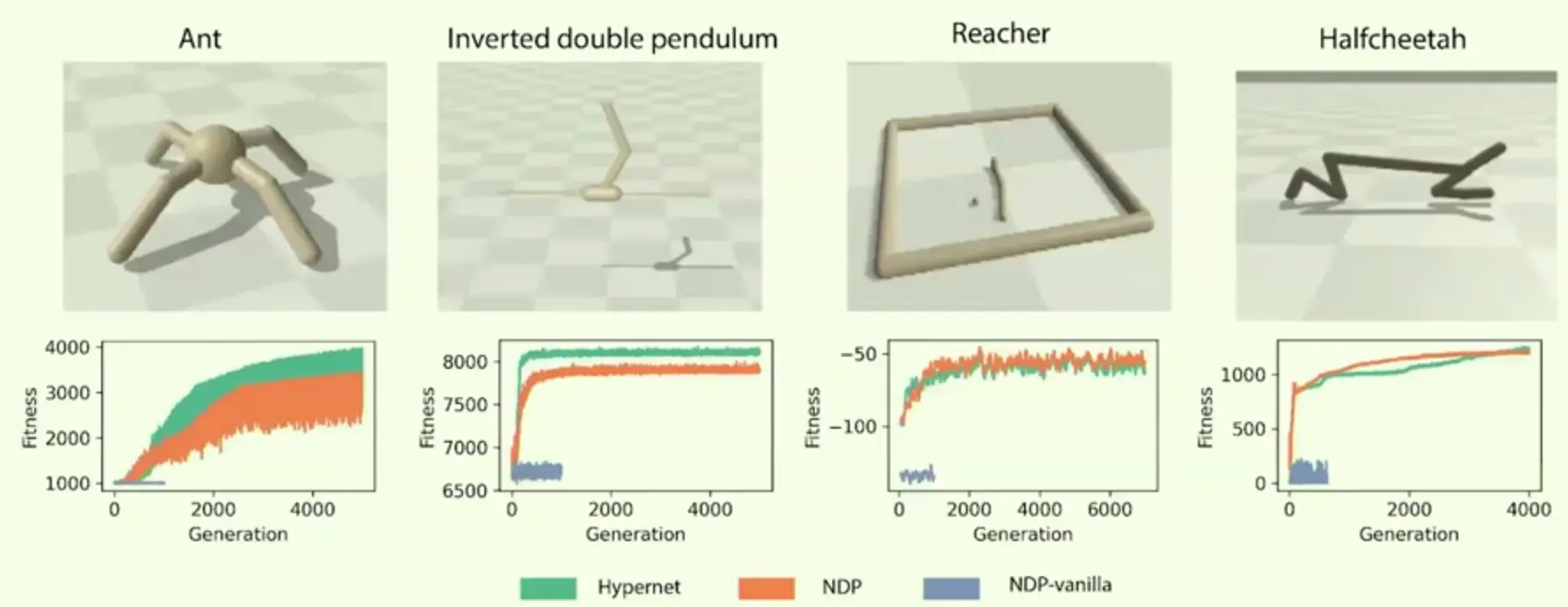
Outperforms regular NDPs, but standard hypernetworks work similarily / better.

→

In what situations is neuronal diversity useful / necessary?

Footnotes

1. Edges = weights, cells = neurons + fixed activation functions. They use ReLU for hidden nodes and linear for outputs. ↩

2. The direct encoding is provided as a baseline that is known to perform well in the tasks we examine and, therefore, serves as an expected upper threshold for fitnesses. As these tasks do not pose any particular need for generalisation or robustness we do not expect to see indirect encodings outcompeting direct ones.

   ↩

3. I.e. a fixed architecture whose weights are produced by a separate model conditioned on neuron tags. Differences to the main method are thus: No growth steps, no DiffModel, no GenModel, no inhibition, one-time mapping to a deterministic fixed topology (given tags + I/O order), only weight assignment is learnt by the EdgeModel. ↩