hamming distance

The Hamming distance between two binary strings of the same length is the number of positions where the corresponding bits differ.

In a set of codewords (binary strings used to represent information), the minimum Hamming distance between any two codewords plays a crucial role. The larger the minimum Hamming distance, the more robust the code is to errors, as it allows detection of more bit-flip errors and, potentially, their correction.
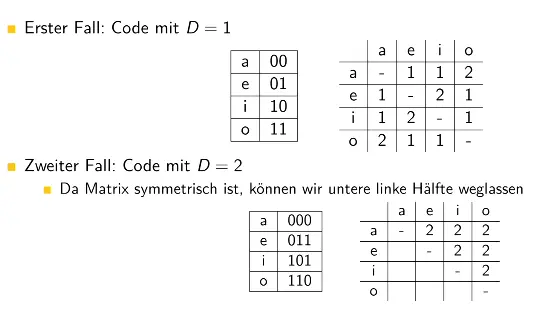
The distance for two codes is defined as:

$$\begin{array}{rl}\text{Hamming distance: }& d_H(x,y)=\sum _{i=1}^n|x_i-y_i|\end{array}$$

For any number of codes, the distance is:

$$\begin{array}{r}{d}_H=\underset{i\ne j}{\min }{d}_H(x_i,x_j)\end{array}$$

For codes with a hamming distance $d_H$, we can detect up to $d_H-1$ errors and correct them if we have $k<\frac{d_H}{2}$ errors (where we just need to find the closest codeword to the received word).

EXAMPLE

Note: The second example has a hamming distance 1 higher because we added a parity bit.

References

error-correcting codes