metric

Metric space

A metric space is an ordered pair $(M,d)$ where $M$ is a set and $d$ is a metric on $M$, i.e. a (“distance/metric”) function $d:M\times M\to \mathbb{R}$, satisfying the following four axioms $\forall x,y,z\in M$:

1. identity of indiscernables: The distance from a point to itself is zero: $d(x,x)=0$
2. Positivity: The distance between two distinct points is always positive: $x\ne y⟹d(x,y)>0$
3. Symmetry: The distance from $x$ to $y$ is always the same as the distance from $y$ to $x$: $d(x,y)=d(y,x)$
4. The triangle inequality holds: $d(x,z)\le d(x,y)+d(y,z)$

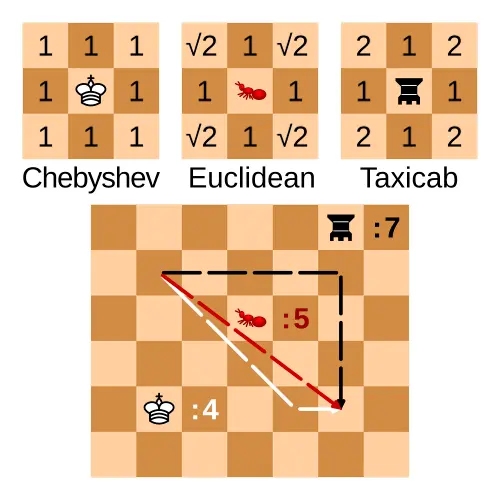
Common distances that are proper metrics

manhattan distance ($L^1$): $d(x,y)={\sum }_i|x_i-y_i|$ - “taxicab” distance on a grid
euclidean distance ($L^2$): $d(x,y)=\sqrt{{\sum }_i(x_i-y_i{)}^2}$ - the “straight line” distance
Chebyshev distance ($L^{\infty }$): $d(x,y)={\max }_i|x_i-y_i|$ - maximum coordinate difference
hamming distancen: Number of positions where symbols differ (for strings/vectors of equal length)
graph geodesic: Shortest path length between nodes (satisfies all metric axioms on the graph)
cosine distance: $1-\cos (\theta )$ where $\theta$ is angle between vectors (metric for normalized vectors)
Jaccard distance: $1-\frac{|A\cap B|}{|A\cup B|}$ for sets A, B
levenshtein distance : Minimum edits to transform one string into another
Wasserstein distance: Optimal transport cost between probability distributions
Hausdorff distance: Maximum distance from any point in one set to its nearest neighbor in another set