neuron

Neurons are just cells.
The soma is the cell body, the dendrites are the input, the axon is the output.

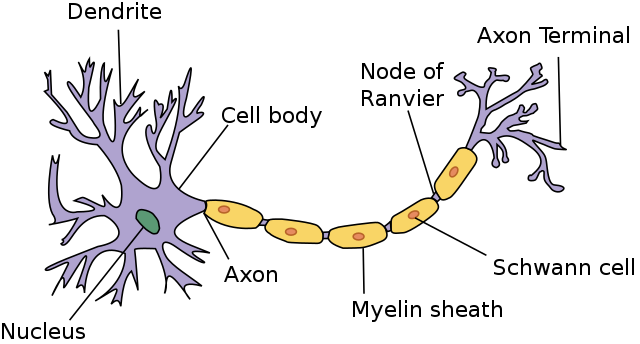
high level properties

Neurons typically have in the range of 5k-35k synapses.

A cerebral pyramidial neuron —the sort of cell we’re reading, writing, and thinking with right now—receives up to 40,000 inputs from other neurons. A spinal motor neuron—the sort that controls our muscles—has about 100,000 inputs.

Neurons are time-based prediction engines.

Synapses close to the soma have a stronger effect on the neuron. If they fire, the neuron is likely to also fire.
Synapses further away, even if many of them - say 20 - fire at the same time, will not get the neuron to fire alone. However, they raise the probability of the neuron firing.
They prepare the neuron to fire, so to say, such that it can fire just a little bit sooner than it would have otherwise, giving it an advantage over other neurons. This neuron can now trigger (the very fast) inhibitory neurons, leading to a different representation, one that matches this neuron’s prediction. This also leads to a sparser representation, which is much more specific.
Networks of these neurons can do sophisticated temporal predictions.

Synapses: unreliable, low precision (almost binary)

Synapses are very unreliable. You cannot assign any precision to them - not even one-digit.
Real neurons don’t change synapse weights accurately, but form new synapses and rely on 10-20 of these almost binary synapses to fire at the same time to get the neuron to fire (sparse pattern based, not numerical precision).
The number 10-20 is derived mathematically, these many are needed for the brain to be robust to noise and fallout - these number have also been observed in experiments.

Sparse population codes

About 2% of neurons are active at a time, at any time, in any part of the brain.
Any single neuron alone being active does not matter that much (although it can ofc. trigger chain reactions).
What matters are sparse activity patterns of many (~ 200) neurons firing together.
This is a very robust way to represent information, because if you have millions of neurons, in order for one representation to look similar to another one, you’d have to change not a few, but hundreds of neurons, so it also doesn’t matter if a few die, spasm, don’t activate, …

Neurons are like telegraph cells, evolved for animals to transmit information quick enough, in order to control muscles, but they don’t do anything fundamentally diffeerent than all other cells.

But telegraphs are not the only thing that matters - to undestand society, you can’t just look at the telegraphs (one of the reasons our connectome simulations don’t work - they are just a small component of the information process system in our brain).

electrical properties

Neurons have a strong negative membrane voltage ( $V_{M} = 60 to 80 mV$ ; resting potential).

Depolarize → more positive voltage than resting potential
Hyperpolarize → more negative voltage than resting potential

Neurons are highly permeable to $K +$ at rest.
But there is a balance between the negative electrical froce which draws the potassium in and the increasing concentration of $K +$ .
Nernst potential ( $V_{M} = - 62 mV$ )→ balance point with no net movement of $K +$ :

E_{k} = \frac{RT}{z F} ln (\frac{[ K ^{+} ] _{out}}{[ K ^{+} ] _{in}})

$E_{k} \dots$ equilibrium/resting potential
$\frac{[ K ^{+} ] _{out}}{[ K ^{+} ] _{in}} \dots$ ratio of ion concentrations in- vs. outside of the cell
$R \dots$ gas constant
$T \dots$ temperature in Kelvin
$F \dots$ Faraday constant
$z \dots$ valence of the ion( $z_{K^{+} or P^{+}} = + 1; z_{C l^{-}} = - 1$ )
$R, T, F$ are approximately standard for most animals most of the time.
At room temperature: $\frac{RT}{F} = 25 mV$ , which we can use as a constant mostly.

If there are other ions at play, we need to account for the differing permiability coefficients of the ions, with a weighted sum (GHK equation):

E_{M} = \frac{RT}{F} ln (Cations \frac{\sum _{j} P _{M_{j}} [ M _{j}^{+} ] _{o u t}}{\sum _{j} P _{M_{j}} [ M _{j}^{+} ] _{in}} + Anions \frac{\sum _{k} P _{A_{k}} [ A _{k}^{-} ] _{in}}{\sum _{k} P _{A_{k}} [ A _{k}^{-} ] _{out}})

$E_{M} \dots$ equilibrium potential of the membrane
$P_{M_{j}} \dots$ permiability of ion $i$

Note: for anions, the ratio is flipped

The effect of a negative ion moving in is the opposite of a positive ion moving into the membrane.

The above equation is only valid for ions with a valence of 1

e.g. fine for $N a, K, Cl, \dots$
TODO what is the modification for different valence level?

Plausible concentration scenario:

Ion	Outside Concentration	Inside Concentration	$V_{ion}$
$K +$	$5 m M$	$100 m M$	$- 80 mV$
$N a +$	$150 m M$	$15 m M$	$+ 60 mV$
So we can see, that potassium wants to leave and sodium want to enter the cell.
![[Neuron-20240225163315980.webp	276]]
But the cell needs to maintain the energy difference, between the inside and outside environment at $- 62 mV$ . To keep this resting equilibrium, where sodium wants to go in and potassium wants to leave, we need to expend energy.

sodium-potassium pump

This pump is one of the primary reasons for the brain using $20%$ of the body’s energy at rest.
Every pump cycle, three sodium ions are pumped out - against the electrical gradient - at the expenditure of energy in the form of one ATP, while 2 potassium ions are pumped into the cell.

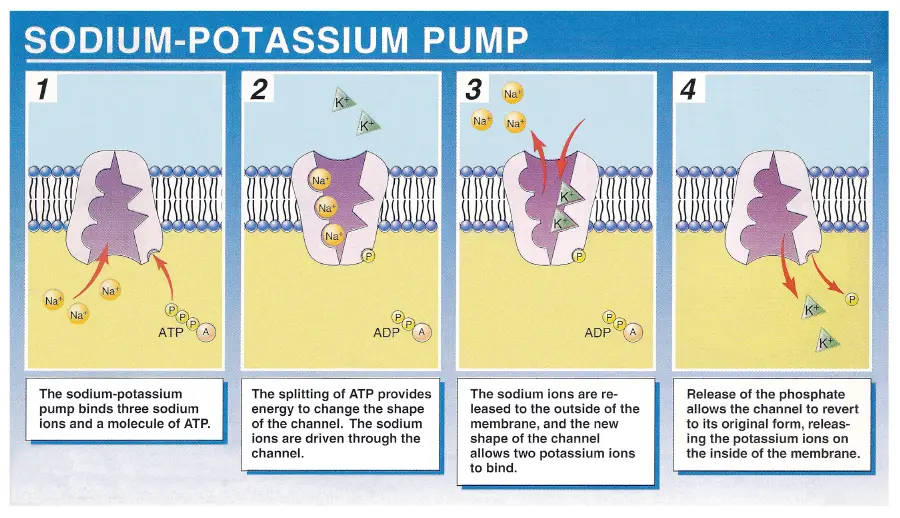
$ATP + H_{2} O \leftrightarrow ADP + P_{i} \approx \frac{40 k J}{m o l}$

Fun-fact: About $3 \times 1 0^{9} ATP$ molecules are used per neuron, per second.

ohm’s law

… interpreted for the neuron

I = \frac{V}{R} = V g

Current in the case of a neuron is the net flow of ions in and out of the cell.
The conductance $g$ is determined by the number of open ion channels.
The ion flow is proportional to some voltage and the number of open ion channels through which ions can pass.
$V$ is not just the voltage of the membrane, but the difference of the current membrance voltage and the equilibrium potential (voltage).
e.g. for potassium:

I_{K^{+}} = (V_{M} - E_{K^{+}}) g_{K^{+}}

If no channels are open or the equilibrium is already reached, the ion flow is $0$ .
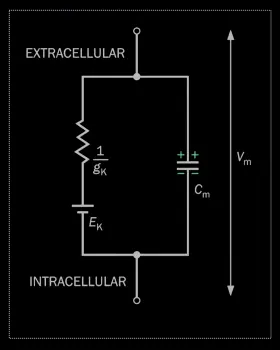
This is equivalent to an RC circuit:
center
Each ion can only go through the respective ion-channel, the ion-flows are independent of eachother:

\displaylines I_{K^{+}} = (V_{M} - E_{K^{+}}) g_{K^{+}} I_{C l^{+}} = (V_{M} - E_{C l^{+}}) g_{C l^{+}} I_{N a^{+}} = (V_{M} - E_{N a^{+}}) g_{N a^{+}}

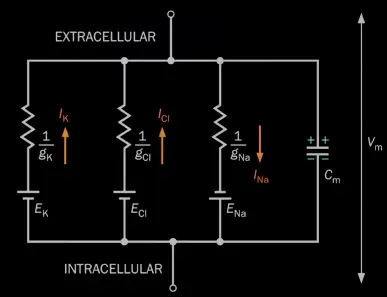
center

ion channels

determines the conductance (can ion flow happen or not; how much)
selective for ion type (big ones don’t fit into small ones and vice-versa)
not selective for direction (if open, ions pass both ways)

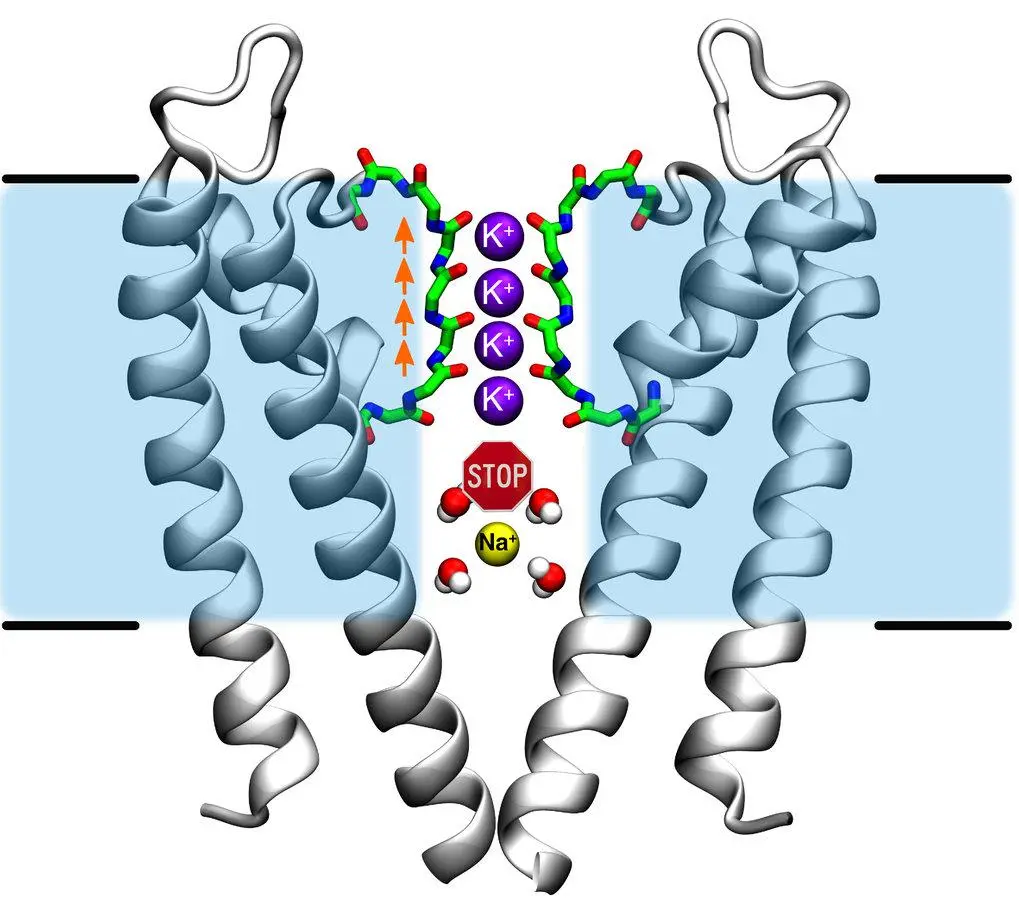
e.g. for $K +$ , there are four protein helices, which stabilize the ions as they pass through the protein pore (long double-helix tube), interacting with the carbonyl groups on the protein backbone (they mimic $K +$ ’s interaction with water). Smaller $N a +$ ions don’t fit.

current injection

What happens when a current is induced externall, e.g if a flash of light hits your photoreceptor?
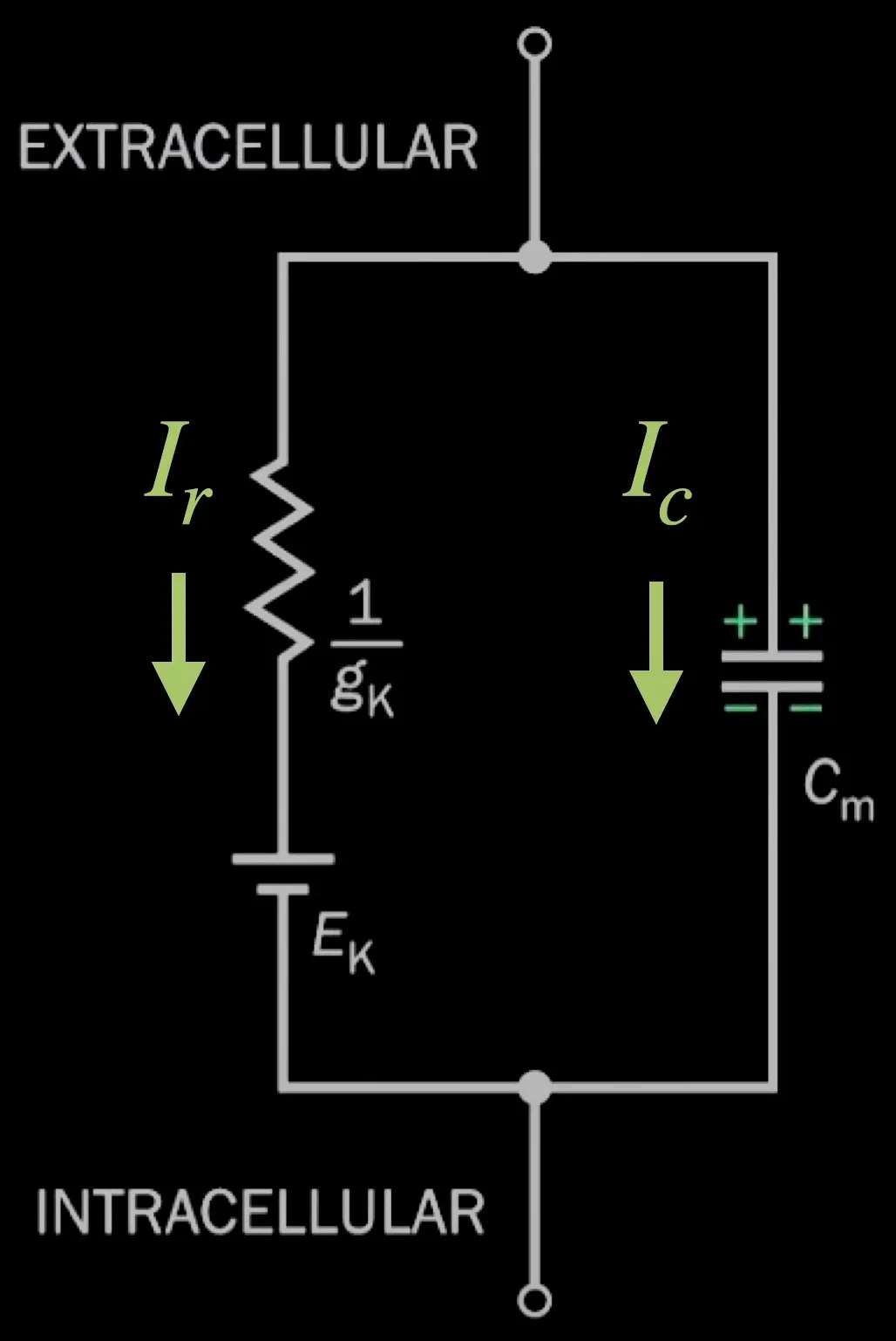
center

\displaylines I_{m} = I_{r} + I_{c} = g_{K} V_{m} + C_{m} \frac{d V _{M}}{d t} = I_{ext}

$I_{m} \dots$ membrane current (total net current)
$I_{r} \dots$ current going through the restistive pathway ( $g_{k} V_{m}$ )
$I_{c} \dots$ current going through the capacitive pathway
$I_{c}$ is injected across the intra and extracellular terminals, through a capacitor, it is determined by the Capacitance of the membrance $C_{m}$ time the rate of change of the membrane potential.
$I_{ext} \dots$ injected current (!!?TODO idk why it is equal?!!)

We solve the above differential equation for $V_{m}$ :

V_{m} (t) = I_{ext} \frac{1}{g _{K}} (1 - exp (- \frac{t}{R _{K} C _{M}}))

$R_{K} \dots$ resistance
$R_{K} C_{m} = τ \dots$ time constant of response. For most neurons $1 < τ < 100$ ms.

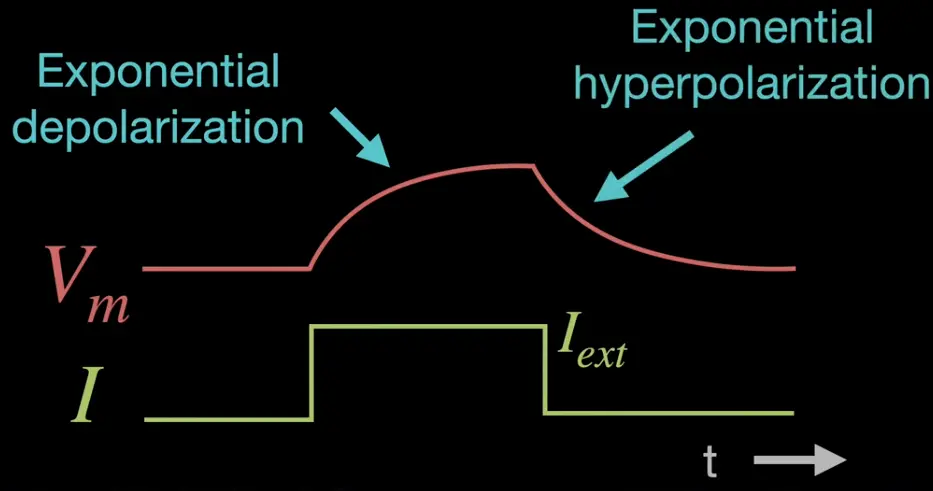
center

Exp. depolarization phase: Voltage induced
Exp. hyperpolarization phase: Voltage “decays”
The amount that the voltage increasesis proportional to the injected current and inversly proportional to the conductance (number of open channels).

The response time to an injected current is in correspondence with $τ$ , which is nearly instantaneous. Smaller $τ$ means faster response times. $τ$ is influenced by the following cellular properties:

g_{K} = \frac{1}{R _{K}} = N γ

$N \dots$
-) Densitiy of channels (higher density, lower $τ$
-) Area (larger Area, lower $τ$ )
$γ \dots$ single channel conducance

neuron shapes

so far we have assumed neurons are … spheres
but neurons are the opposite, very long, many branches
their job is to quickly get information across the brain, their “wires” stretching long distances
so let’s approximate them not as a sphere, but as a cylinder
so far we only looked at the change in time, now we also need to take (voltage) changes in space into account

$d t \dots$ change in time
$d x \dots$ change in axial direction

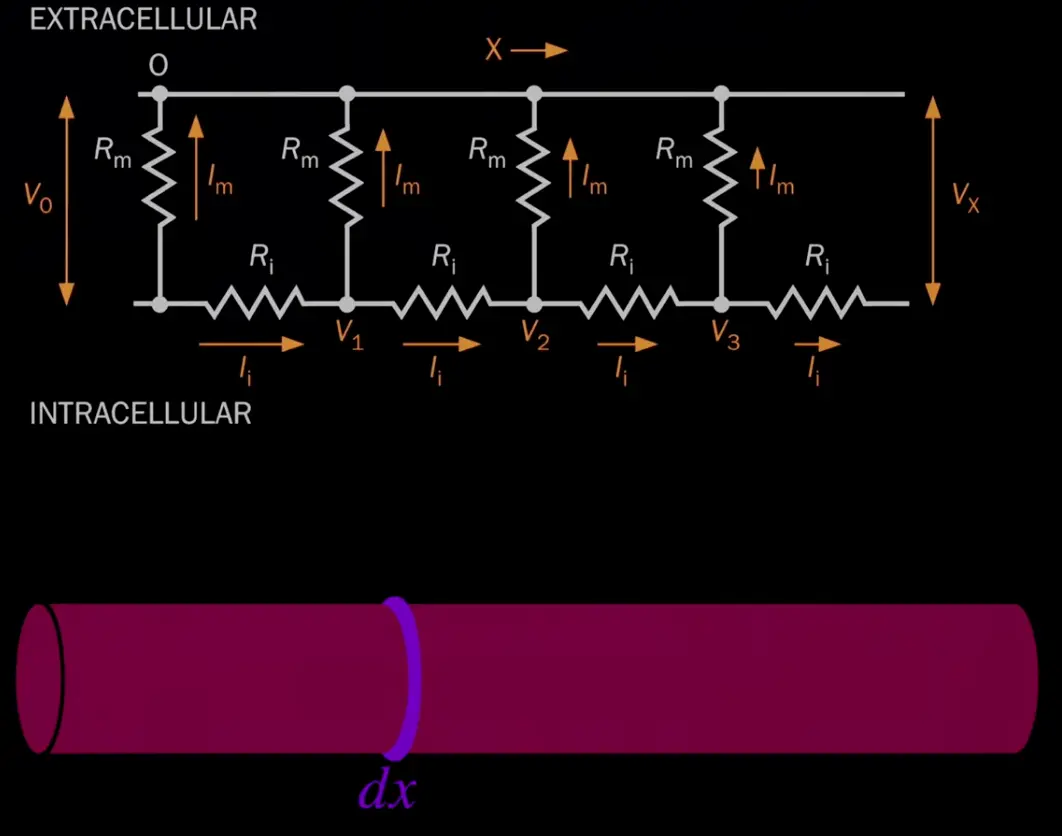
center

Currents can flow along the axial direction (inside the cell, $I_{i}$ ) and they can flow through the membrane, through channels ( $I_{m}$ ).
The circuit diagram shows how a middle piece (ignoring ends for now) is chopped up into little $d x$ .

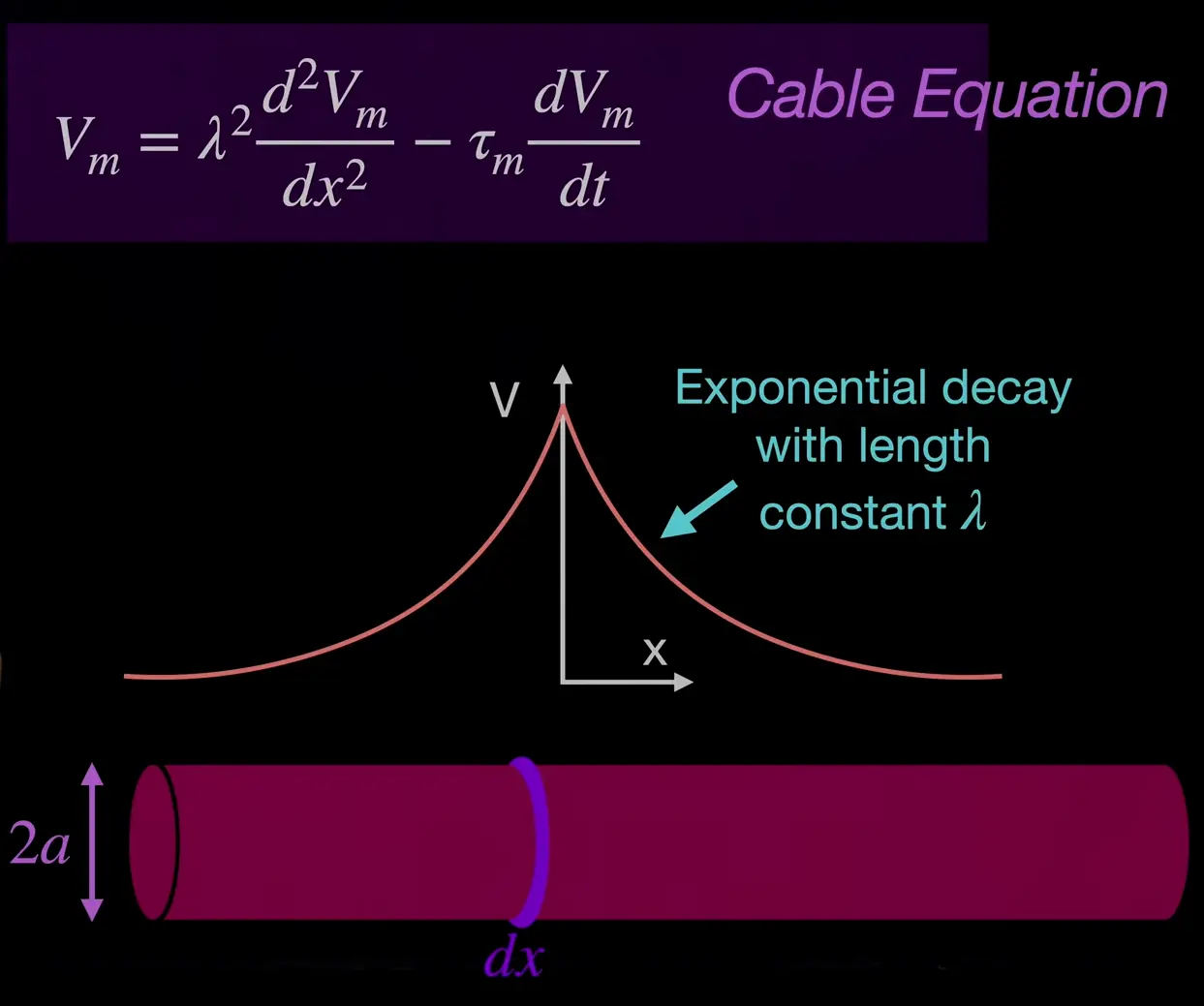
cable equation

We somehow reformulate ohm’s law (details not as important for now ig):
$I_{m} = \frac{V _{m}}{R _{m}} + C_{m} \frac{d V _{m}}{d t}$
$I_{m} = - \frac{d I _{i}}{d x}$
$R_{i} I_{i} = - \frac{d V _{m}}{d x}$

The cable equation is a partial differential equation (first derivative of time and second derivative of space).

V_{m} V_{m} = \frac{R _{m}}{R _{i}} \frac{d ^{2} V _{m}}{d x ^{2}} - R_{m} C_{m} \frac{d V _{m}}{d t} = λ^{2} \frac{d ^{2} V _{m}}{d x ^{2}} - τ_{m} \frac{d V _{m}}{d t}

$λ^{2} \dots$ length constant of propagation … ratio between conductivity of membranve vs. conductivity of intracellular salty water space

new notation regarding $r$ and $R$ from now on

… $R$ will mean bulk properties and $r$ will mean “patchy” properties; per area

$a \dots$ radius of the cable / cylinder (this can vary!)
$R_{m} = \frac{r _{m}}{2 πa}$ … membrane restistance = resistance at patch / cylinder circumference
$R_{i} = \frac{r _{i}}{π a ^{2}}$ … axial resistance = resistance at patch / cylinder crossection area

λ^{2} = \frac{R _{m}}{R _{i}} = \frac{r _{m}}{r _{i}} \frac{a}{2}

larger cylinder (larger $a$ ) $\to$ voltage travels further
however, a larger axon also requires more upkeep (energy/atp, …)

550|center

Images

References

Why do neurons have an electric charge? | Nernst Potential | Resting Potential of Neurons
Active Properties of Neurons | Responses to Current | Cable Equation in Axon Conduction

https://www.quora.com/How-many-input-action-potentials-out-of-about-10-000-inputs-does-a-neuron-typically-need-to-receive-in-order-fire-Whats-the-average-time-distance-between-these-input-spikes-and-how-often-do-neurons-typically-fire

https://qbi.uq.edu.au/brain/brain-anatomy/types-neurons
https://qbi.uq.edu.au/brain/brain-functions/what-are-neurotransmitters
https://qbi.uq.edu.au/brain-basics/brain/brain-physiology/action-potentials-and-synapses
https://qbi.uq.edu.au/brain/brain-anatomy/axons-cable-transmission-neurons

Max Wolf's Second Brain

Explorer

neuron

high level properties

electrical properties

sodium-potassium pump

ohm’s law

ion channels

current injection

neuron shapes

cable equation

Images

References

Graph View

Table of Contents

Backlinks