norm

Norm

Given a vector space $X$ over a subfield of the complex numbers, a norm is a function $\Vert \cdot {\Vert }_p:F\to {\mathbb{R}}^{+}$ with the following properties:

• positive definiteness

• absolute homogeneity

• triangle inequality

$p^{th}$ norm:

$$|x{\Vert }_p=(\sum _{i=1}^n|x{|}^p{)}^{\frac{1}{p}}$$

We take the absolute value of $x$ because uneven $p$ could yield negative values.

The norm tells us the size of a mathematical object in a certain space.
Length usually refers to the 2-norm, but there are other norms as well.

The $p$-norms in 2D look like this (showing the unit circle for each norm, i.e. all points with norm = 1):

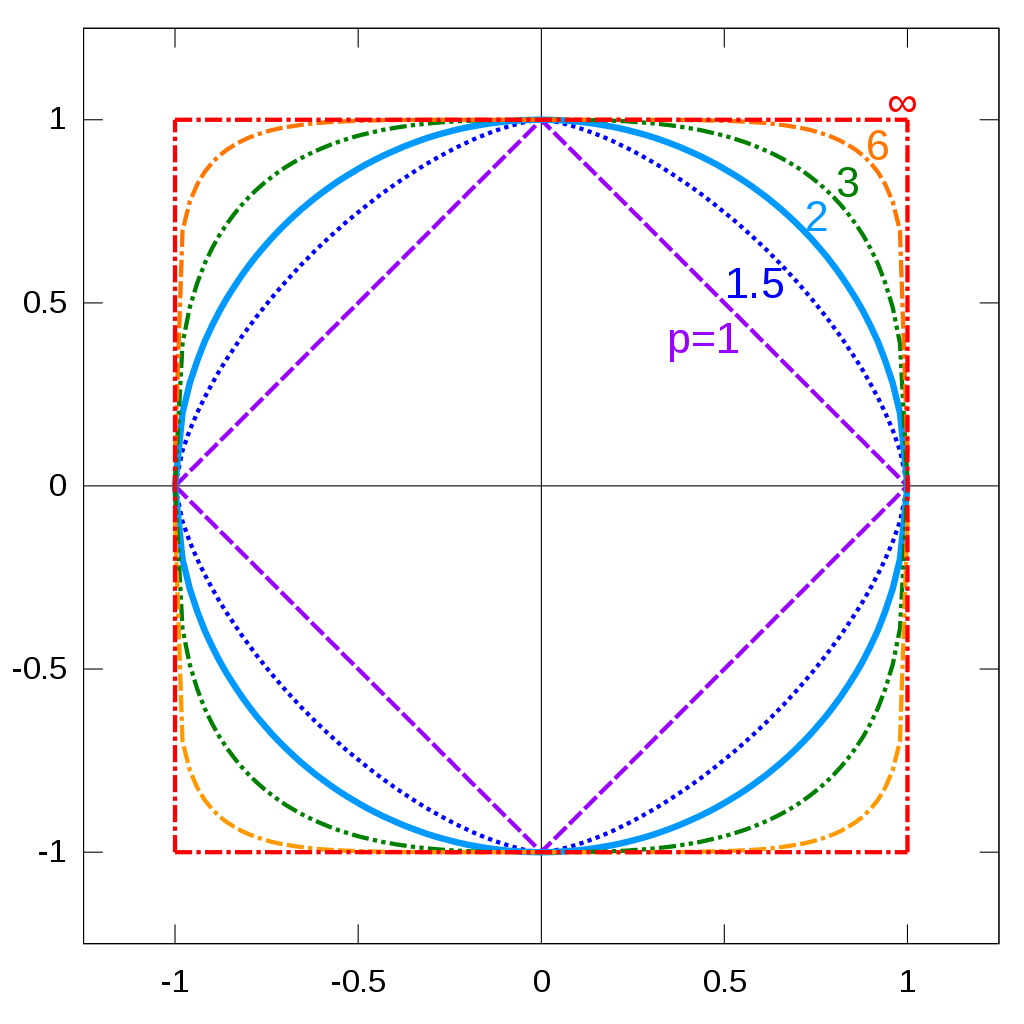
$p<0$ is not a norm because it violates the triangle inequality.
$p=0$ is not a norm because it is not positive definite; it is the hamming distance – counting the number of non-zero elements in a vector.
$p=1$ is also reffered to as taxicab norm because with that norm, it is like driving through city blocks (straight lines, no diagonals). You’re adding up the absolute values/distances to zero of each component.
$p=2$ is also known as the euclidean norm. It is the most common norm, measuring the straight-line distance from the origin to the point in space. It’s derived from the pythagorean theorem; it smoothes out the corners of the 1-norm.
$p\to \infty$ is also known as the maximum norm because it only cares about the largest value in the vector.

https://en.wikipedia.org/wiki/Lp_space

Info

A norm induces a metric via $d(x,y)=\Vert x-y\Vert$.

References

Visualizing the circles of p-norms (Medium)