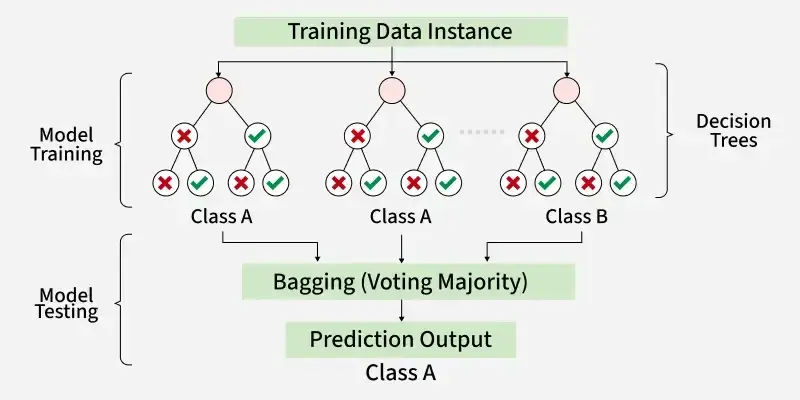
random forest

Random Forest

An ensemble of decision trees, each trained on a random subset of data and features.
Predictions are aggregated by majority vote (classification) or averaging (regression).

Two sources of randomness decorrelate the trees:

1. Bootstrap sampling (bagging ¹): Each tree trains on a random sample with replacement from the training data

2. Feature subsampling: At each split, only a random subset of features (typically $\sqrt{d}$ for classification) is considered

   Final prediction: $\hat{y}=\text{mode}({\hat{y}}_1,\dots ,{\hat{y}}_T)$ for classification, or $\frac{1}{T}{\sum }_t{\hat{y}}_t$ for regression.

Individual trees are intentionally deep/overfit (high variance, low bias). But because the randomization makes their errors uncorrelated, averaging reduces variance without increasing bias.

Why decorrelation matters

If $T$ trees each have variance ${\sigma }^2$ and pairwise correlation $\rho$, the ensemble variance is:

$$\text{Var}\left(\frac{1}{T}\sum _t{\hat{y}}_t\right)=\rho {\sigma }^2+\frac{1-\rho }{T}{\sigma }^2$$

The second term vanishes as $T\to \infty$, but the first doesn’t. Feature subsampling reduces $\rho$—this is why random forests outperform simple bagging (which only uses bootstrap sampling).

Practical notes

More trees always helps (or plateaus)—unlike many hyperparameters, there’s no overfitting risk from adding trees, just computational cost.

Feature importance: Measure the increase in prediction error when a feature’s values are randomly permuted. Features the forest relies on show large error increases.

Out-of-bag error: Since each tree only sees ~63% of samples (due to bootstrap), the remaining samples provide a free validation set for that tree.

Footnotes

1. BAGGING = Bootstrap AGGregatING but it also results in multisets since samples can be repeated. ↩