roots of unity

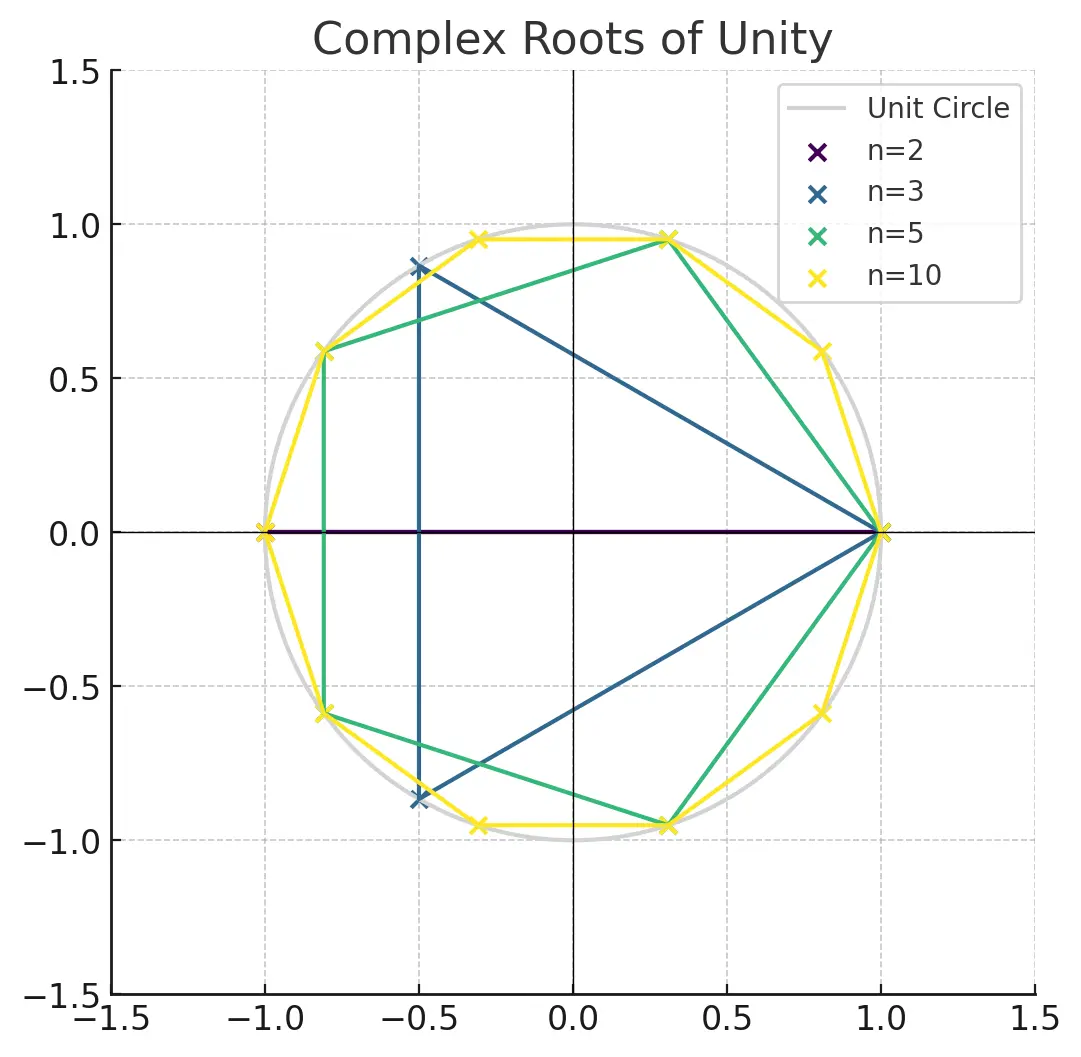
A root of unity is any complex number that, when raised to a positive integer power $n$, equals $1$.

$z\in \mathbb{C}$ is an $n^{\text{th}}$ root of unity if:

$$\begin{array}{r}{z}^n=1\end{array}$$

These roots are evenly spaced on the unit circle in the complex plane and can be represented as:

$$\begin{array}{r}{\zeta }_n^k=e^{2k\pi i/n}=\cos \left(\frac{2\pi }{n}\right)+i\sin \left(\frac{2\pi }{n}\right)\end{array}$$

for $k=0,1,\dots n-1$. The angles between the consecutive roots are all equal, and their magnitudes are all equal to $1$–they lie on the unit circle, hence roots of unity.

3b1b: generating functions shows an application of roots of unity.

For any root of unity ${\zeta }_n^k$, multiplying it by itself $n$ times gives us 1.

E.g. for the 5th roots of unity ${\zeta }_k=e^{2\pi ik/5}$ and their powers: ${\zeta }_1=e^{2\pi i/5}$ (rotation by 72°):

$${\zeta }_1\to {\zeta }_1^2\to {\zeta }_1^3\to {\zeta }_1^4\to {\zeta }_1^5=1$$

${\zeta }_2=e^{4\pi i/5}$ (rotation by 144°):

$${\zeta }_2\to {\zeta }_2^2\to {\zeta }_2^3\to {\zeta }_2^4\to {\zeta }_2^5=1$$

${\zeta }_3=e^{6\pi i/5}$ (rotation by 216°):

$${\zeta }_3\to {\zeta }_3^2\to {\zeta }_3^3\to {\zeta }_3^4\to {\zeta }_3^5=1$$

${\zeta }_4=e^{8\pi i/5}$ (rotation by 288°):

$${\zeta }_4\to {\zeta }_4^2\to {\zeta }_4^3\to {\zeta }_4^4\to {\zeta }_4^5=1$$

${\zeta }_5=e^{10\pi i/5}=1$ (rotation by 360°):

$$1\to 1\to 1\to 1\to 1$$

Each root, when multiplied by itself repeatedly, traces out its own unique path through the fifth roots before arriving at 1 after exactly five multiplications.