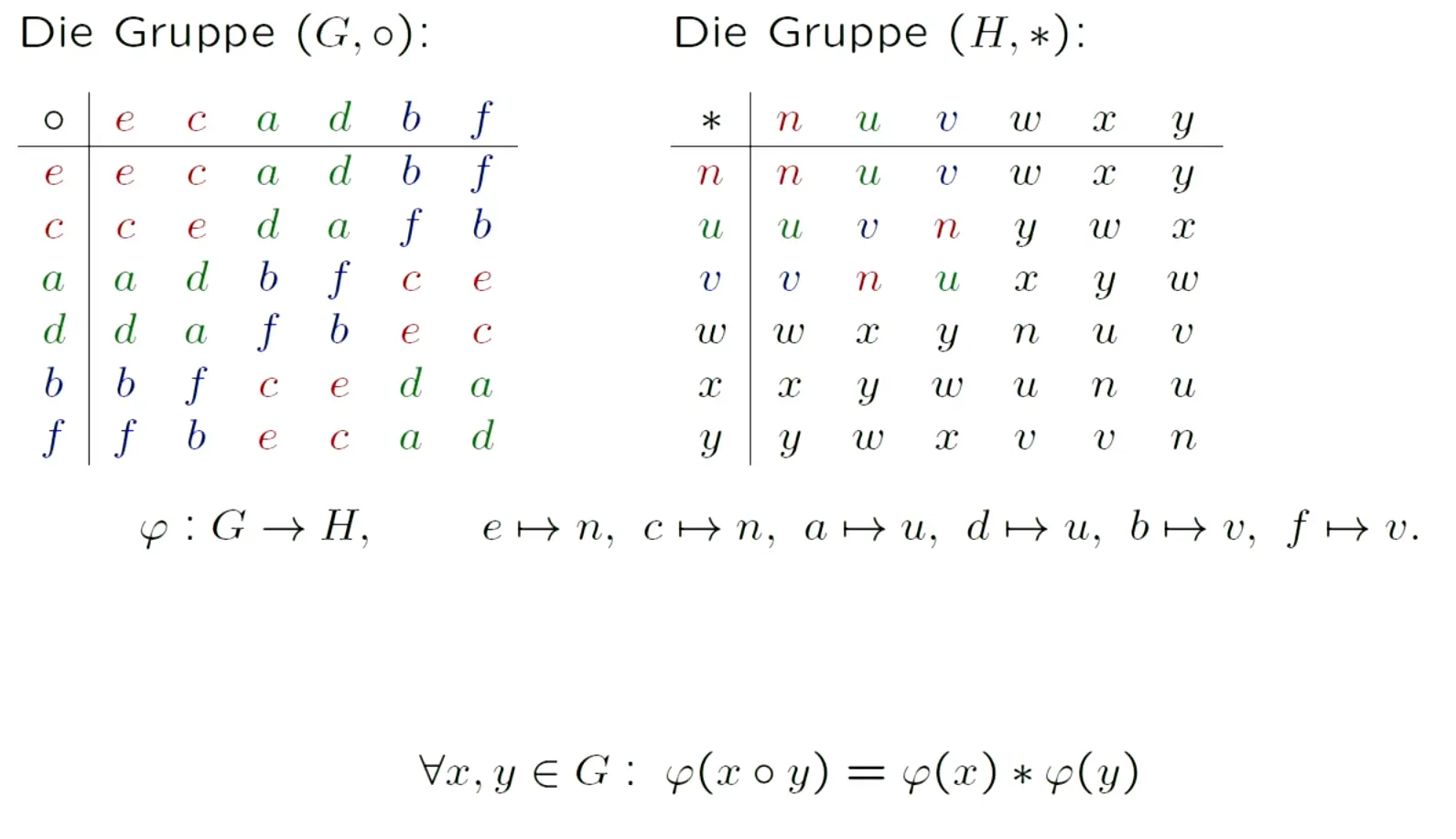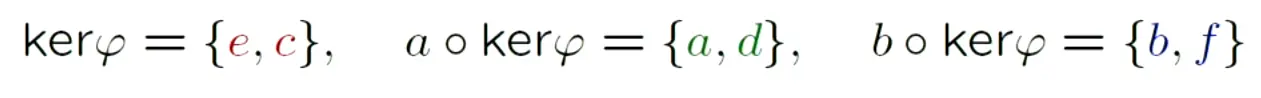A homomorphism is a morphism on algebraic structures that preserves the operations defining the structure.
Group Homomorphism
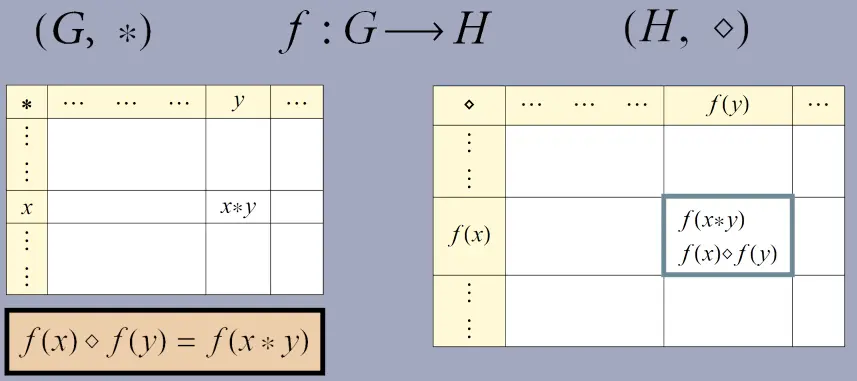
Let be groups. A function is a homomorphism if it preserves the group operation:
When clear from context, we often write both operations as or drop the symbol entirely.
Homomorphisms preserve structure
Applying after gives the same result as applying to each element and then using .
For example: and
Properties of Homomorphisms
For any homomorphism :
The identity maps to the identity
Proof:Inverse of maps to inverse of :
Suppose is not 1-1 (injective):
Then, and
→ there’s more than one element that maps to the identity
This leads us to the definition of the kernel:
Kernel and Image
For a homomorphism , the kernel and image are defined as:
The kernel contains all elements that map to the identity in , while the image contains all elements in that are “reached” by .
Note: The notation doesn’t mean inverse, but preimage, i.e. the set of all elements “inputs” that map to .
The kernel is the degree to which the homomorphism “fails to be one-to-one”, i.e. "collapses" the group structure - a trivial kernel ( ) means no collapsing occurs and distinct elements remain distinct (injection). The image tells us how much of is "covered" by the homomorphism - if , then every element in is reached (surjection).
Link to originalNormal subgroup
For a group and subgroup , the following are equivalent:
- is normal:
- ( is closed under conjugation)
- : (left and right cosets form the same partition, i.e. are equal)
For a commutative group, e.g. abelian groups, this is trivially satisfied for any subgroup → all subgroups are normal.
Proof: We show : “”: (“von links”) “”: (“von rechts”) (Voraussetzung) And →
homomorphism, and
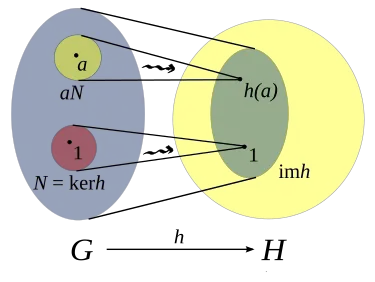
If we have a homomorphism from to , then the image of under is a subgroup of and the kernel of is a normal subgroup of .
Proof: First show :
- is non-empty since
- : so
- : so
- : so
Properties 1-3 show is a subgroup, and property 4 shows it’s normal.
For , similar subgroup test shows it’s closed under operations and contains inverses.
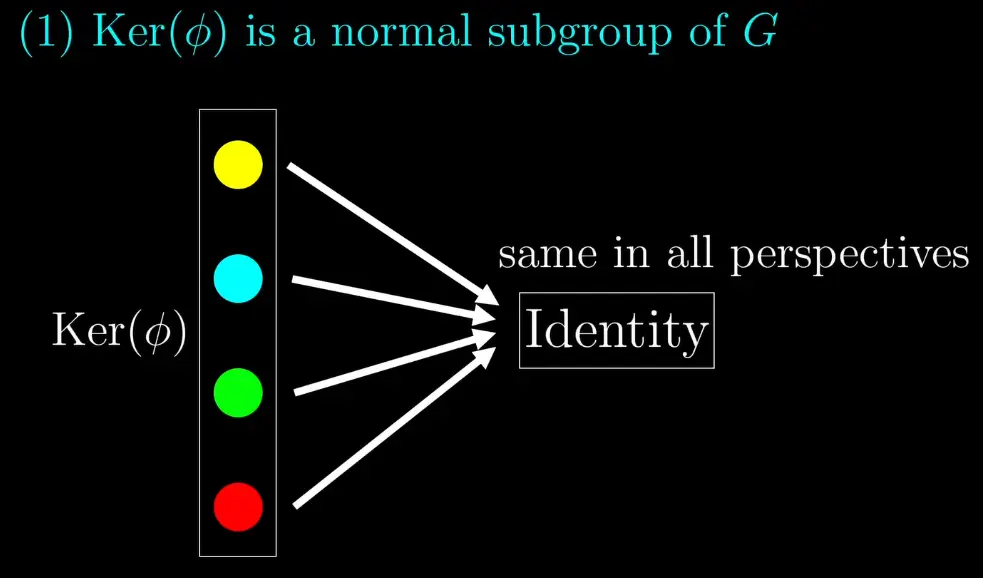
The kernel maps to the identity, which is the same in all perspectives, and is always a normal.
Visual intuition for the above: Imagine as a "filter" that maps elements from to . The kernel is the set of elements that "disappear" when passing through the filter, while the image is the set of elements that "make it through". The filter however is "well-behaved" in the sense that it preserves the group structure.
In this example, we have an injective homomorphism that isn’t surjective, embedding a group into a biger group. It is also an isomorphism to a subgroup of the codomain (target group).
(source)
This is a surjective homomorphism that isn’t injective, collapsing elements into a smaller group, i.e. the image is all of the codomain, but the kernel is non-trivial (contains elements other than the identity identity … that map to the identity).
The big picture is not an isomorphism, beceause the mapping is not bijective (not the same number of elements in the domain and codomain). However, there is an isomorphism between the colors in the domain and codomain, which are the cosets of the domain, as the theorem below shows .
First Isomorphism Theorem
For any homomorphism :
The set of all cosets of the kernel in the group is isomorphic to the image of .
This shows that after “collapsing/factoring out” elements that map to the identity (the kernel), the factor group structure exactly matches the image.
Proof is an isomorphism We need to show that
- is well-defined: (can’t have elements from the same coset point to different elements in )
- is surjective
- is injective
- is a homomorphism
Ad 1: We need to show that if , then and are the same.
This would mean that there is an
Note: when mapped become the identity in as they are in the kernel.Ad 2: Surjectivity is clear as maps all cosets to elements in the image:
Note: is the definition of : maps cosets to elements in the image!Ad 3: For injectivity we want to show that:
In words: The -image of a coset is the same as the -image of the representative of that coset (representative = any element in the coset).
Note: (and we can wrhite – from the left – since the kernel is normal)
→ If the images are the same the preimages are the same.Ad 4:
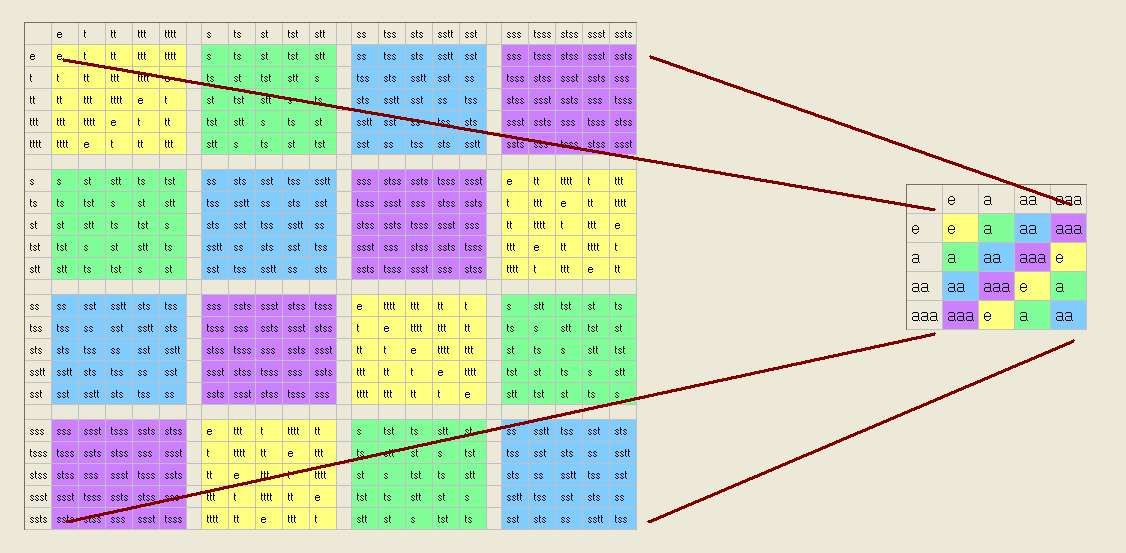
EXAMPLE
Same colors map to the same colors (homomorphism – we can map first and then calculate or first map and then calculate), but not all colors are reached (not surjective – this doesn’t work in the other direction).
The different colors represent different cosets of the kernel! And we can calculate within this factor group.
Here, any green element times any blue element is red, which we can express as .
Now, applying the first isomism theorem, we map the red coset to the red element in the domain, the green coset to the green element, and the blue coset to the blue element:then we have an isomorphism between the factor group and the image:
So calculating with colors in the codomain is isomorph to calculating with cosets in the domain.
The First Isomorphism Theorem with
Consider mapping integers to their remainder mod 4.
The kernel is (multiples of 4).
The quotient group consists of cosets:
The image is all of which is also
The theorem tells us , i.e. arithmetic modulo 4 is the same as working with remainders
Special Types of Homomorphisms
An injective homomorphism is called a monomorphism
A surjective homomorphism is called an epimorphism
A bijective homomorphism is called an isomorphism, denoted
A homomorphism from a group to itself is called an endomorphism
A bijective endomorphism is called an automorphism
Group homomorphism between congruence classes and roots of unity
Consider the groups and where is a primitive root of unity (i.e. the first one that’s not just ).
Define the map:
To verify this is a homomorphism, we check if it preserves the group operation (addition in maps to multiplication in ):
This is a surjective homomorphism since it covers all of .
To find the kernel, we solve for all where:The last step follows because exactly when is an integer.
Applying the First Isomorphism Theorem:
Both and are cyclic groups of order : In we add 1 repeatedly modulo , while in we multiply by repeatedly until returning to 1 after steps.