year: 2010
paper: https://neuro.bstu.by/ai/2010-s-project/nn-1.pdf
website:
code:
connections: HyperNEAT, hebbian learning, indirect encoding, synaptic plasticity, Sebastian Risi, Kenneth O. Stanley
In general a learning rule applies a weight update:
In the most general iterated model, they augment HyperNEAT with pre- and post-synaptic activation, and with the weight value, and have it output a delta to the weight value. At the initial step pre,post and w are set to 0, and the conenctivity is initialized like in HyperNEAT, but the network is also queried every subsequent timestep.
A more restricted model sets the weights of a hebbian ABC(why no D?) model once, setting fixed dynamics for lifetime weight changes:
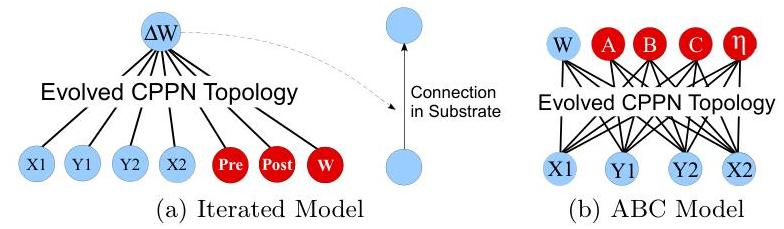
They also test a minimal plain hebbian model:
The models they train have no hidden units, and they train in T-maze with linear and nonlinear reward signatures:
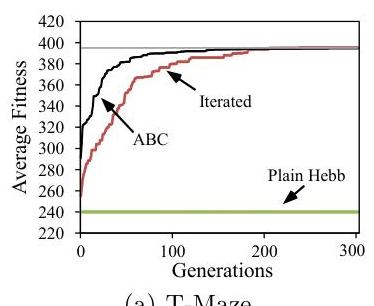
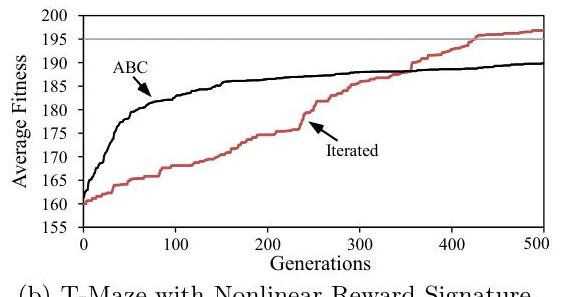
The change in performance over evaluations for both scenarios is shown in this figure. All results are averaged over 20 runs. The horizontal line (top) indicates at what fitness the domain is solved. The iterated and ABC model are both able to solve the standard T-Maze domain (a) in about the same number of generations whereas the plain Hebbian approach does not show the necessary dynamics. The T-Maze domain with a nonlinear reward signature (b) requires a nonlinear learning rule, which only the iterated model discovers.
….
The computational complexity for every time step is O(n) + nO(m), where O(n) and O(m) are the costs of simulating an ANN with n connections and an underlying CPPN with m connections, respectively.
While reading I asked myself why sth like this hasn’t been tried again more recently (like in comparison to Meta-Learning through Hebbian Plasticity in Random Networks).
In a recent talk, Risi mentioned they’re exploring this again! (adding location)