year: 2021/06
paper: https://arxiv.org/pdf/2104.04657
website:
code: https://github.com/google-research/google-research/tree/master/blur
connections: cma-es, hebbian learning, meta learning, backpropagation, VSML, self-organization
TLDR
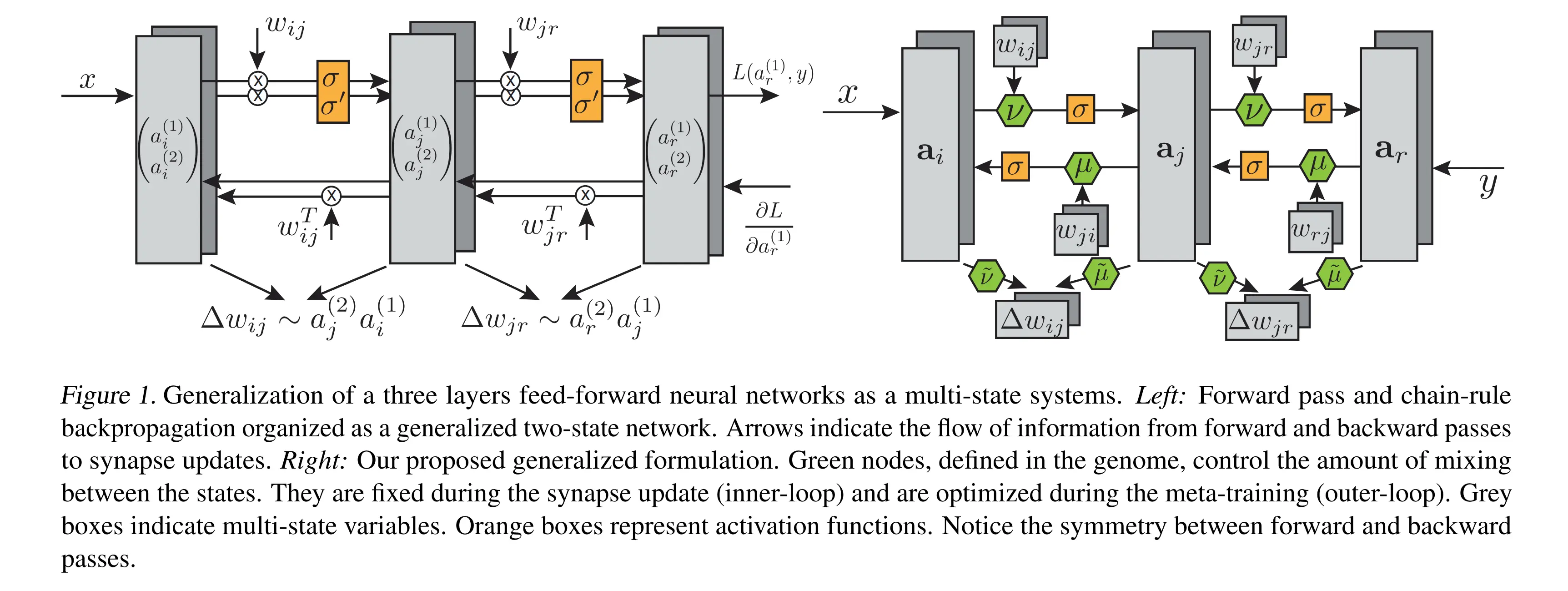
Sandler et al. introduce a new type of generalized artificial neural network where both neurons and synapses have multiple states. Traditional artificial neural networks can be viewed as a special case of their framework with two-states where one is used for activations, the other is used for gradients produced using the backpropagation learning rule. In the general framework, they do not require the backpropagation procedure to compute any gradients, and instead rely on a shared local learning rule for updating the states of the synapses and neurons. This Hebbian-style bi-directional local update rule would only require that each synapse and neuron only requires state information from their neighboring synapse and neurons, similar to cellular automata. The rule is parameterized as a low-dimensional genome vector, and is consistent across the system. They employed both evolution strategies, or conventional optimization techniques to meta-learn this genome vector, and their main result is that the update rules meta-learned on the training tasks generalize to unseen novel test tasks. Furthermore, the update rules perform faster than gradient-descent based learning algorithms for several standard classification tasks. - Survey of Collective Intelligence
What if neurons could store more than just their activation? What if they could simultaneously track multiple pieces of information - like both their forward signal and the error signal flowing backward? BLUR explores this by giving neurons multiple “states” and discovering what update rules emerge.
Backpropagation is secretly Hebbian
During the forward pass, neuron computes:
During backprop, we compute the gradient and update weights:
where is the derivative of the activation function.
This is Hebbian! The update depends on pre-synaptic activity () times post-synaptic activity (). We can reformulate this using two neuron states:
- Forward activation
- Gradient times derivative
Now backprop is just fixed rules for how these states interact.
Generalizing beyond backprop: states per neuron, learned interactions
Instead of hardcoding that neurons have exactly 2 states (activation + gradient), BLUR allows states per neuron.
Instead of fixed rules for how states interact, it learns small matrices that control information flow:Forward pass: Each neuron updates all its states using:
Where:
- : State of neuron (e.g., might be activation, might be error)
- : Channel of the synapse from neuron to (synapses also have multiple channels!)
- : Element of the matrix controlling how state from upstream influences state here
- : Forget gate - how much of the previous state to keep
- : Update gate - how strongly new information affects the state
- : Activation function
- Sum over : All upstream neurons; sum over : All state dimensions
Example: If , only state 1 flows forward (like activations in backprop), while state 2 is isolated.
Backward pass: Similar update but information flows from downstream neurons :
Matrix controls backward information flow. Notice can differ from - forward and backward weights need not be symmetric! Here denotes all neurons downstream of .
Weight update: Generalizes Hebbian learning across all state pairs:
This says: (TODO … had a mistake here)
Forward and backward passes use the same type of update rule, just with different connectivity patterns.
This symmetry is more biologically plausible than backprop’s asymmetry.
The system can discover update rules where information flows bidirectionally during both passes, where weights for forward and backward differ (), or where more than 2 states track different aspects of computation.Since the genome doesn’t encode a loss function, the backward pass just propagates whatever signal you inject at the output layer. During meta-training, this is the true label, but the learned rules generalize to propagate any feedback signal.
These aren't gradient descent in disguise
In gradient descent, if changing weight affects how much we update weight , then the reverse must be equally true - changing must affect ‘s update by the exact same amount. Mathematically:
This symmetry is forced by calculus - if you’re minimizing any function , the order of taking derivatives doesn’t matter: .
But BLUR’s discovered genomes violate this symmetry! The update to might strongly depend on , while ‘s update completely ignores . This proves they’re not minimizing any hidden loss function - they’re doing something fundamentally different.
Traditional optimizers can only move “downhill”. BLUR’s learned rules could temporarily increase loss to escape local minima, exploit asymmetries in forward/backward passes, or optimize for multiple objectives simultaneously (learning speed, final accuracy, robustness). This is why BLUR often learns faster than SGD early in training - it’s following update rules that evolution discovered work well across many tasks, not trying to minimize a specific function.
Meta-learning: Finding the learning algorithm
The “genome” is tiny (~100 parameters) but controls how the entire network learns:
Forget gates : Control memory retention. for neuron states (how much activation/error to keep between updates), for synapse weights (how much of the old weight to retain). means perfect memory, means complete reset.
Update gates : Control learning strength. scales how much new information affects neuron states, scales weight updates. Similar to learning rate but state-specific.
Transform matrices : Route information between neuron states. controls how upstream state influences current state during forward pass. does the same for backward pass. For , backprop uses specific values that keep activations and gradients separate.
Synaptic transforms : Determine which state combinations drive weight updates. weights post-synaptic state , weights pre-synaptic state . Backprop would use values that make activation × gradient produce the update.
Meta-training works by sampling many learning problems: initialize random weights, apply BLUR rules for some steps, evaluate performance. The genome that produces networks that learn well across many problems survives. They use either gradient descent on the genome parameters or evolution strategies (CMA-ES) which treats the genome as DNA to evolve.
Trained only on MNIST digits, they generalize to Fashion-MNIST and letter recognition without modification.
Architectural insights from experiments
Genomes trained on deeper networks (4 layers) successfully train shallower networks (1-3 layers) but not vice versa - suggesting they learn more general update rules when forced to handle deeper credit assignment.
Surprisingly, symmetric single-state synapses with backprop initialization often outperform more complex multi-state variants. The sweet spot seems to be minimal deviation from backprop that adds just enough flexibility to discover better dynamics.
In early training, BLUR consistently outpaces SGD - the learned rules excel at rapid initial learning, though SGD often catches up given enough steps (similar to VSML). This suggests the discovered algorithms optimize for different objectives than minimizing final loss.
Difference to VSML
Both approaches meta-learn update rules, but with different philosophies.
VSML says “replace each weight with a tiny RNN and let them figure out backprop”, while BLUR says “give neurons multiple states and learn the wiring diagram between them”.
BLUR’s genome is more interpretable - you can see which states talk to which during forward/backward passes, but imposes more structure.