Mixture of A Million Experts

year: 2024/07
paper: https://arxiv.org/pdf/2407.04153
website:
code:
connections: Mixture of Experts, scaling laws, product key memory

---

Motivation

…increasing the number of experts is an effective way to improve performance without increasing the inference cost. However, their experiments showed that the efficiency gains provided by MoEs plateau after a certain model size is reached.
More recently, Krajewski et al. (2024) discovered that this plateau was caused by using a fixed number of training tokens. When the number of training tokens is compute-optimal, MoEs consistently outperform dense models in terms of FLOP efficiency. Moreover, they introduced granularity (the number of active experts) as a new scaling axis and empirically showed that using higher granularity improves performance. Extrapolating this fine-grained MoE scaling law suggests that continued improvement of model capacity will ultimately lead to a large model with high granularity, corresponding to an architecture of an immense number of tiny experts.

Beyond efficient scaling, another reason to have a vast number of experts is lifelong learning, where MoE has emerged as a promising approach. For instance, Chen et al. (2023) showed that, by simply adding new experts and regularizing them properly, MoE models can adapt to continuous data streams. Freezing old experts and updating only new ones prevents catastrophic forgetting and maintains plasticity by design. In lifelong learning settings, the data stream can be indefinitely long or never-ending (Mitchell et al., 2018), necessitating an expanding pool of experts..

Totally not inefficient, lol.

Results

This design is supported by the recent discovery of the fine-grained MoE scaling law. To overcome the computational overhead of routing to a large number of experts, we apply the product keys to efficiently select a small subset of hidden neurons within a wide MLP layer. Empirical analysis using language modeling tasks demonstrate that given the same compute budget, PEER significantly outperforms dense transformers, coarse-grained MoEs and product key memory layers.

$$\mathbb{I}={\mathcal{T}}_k(\{q(x{)}^T{k}_i{\}}_{i=1}^N)$$

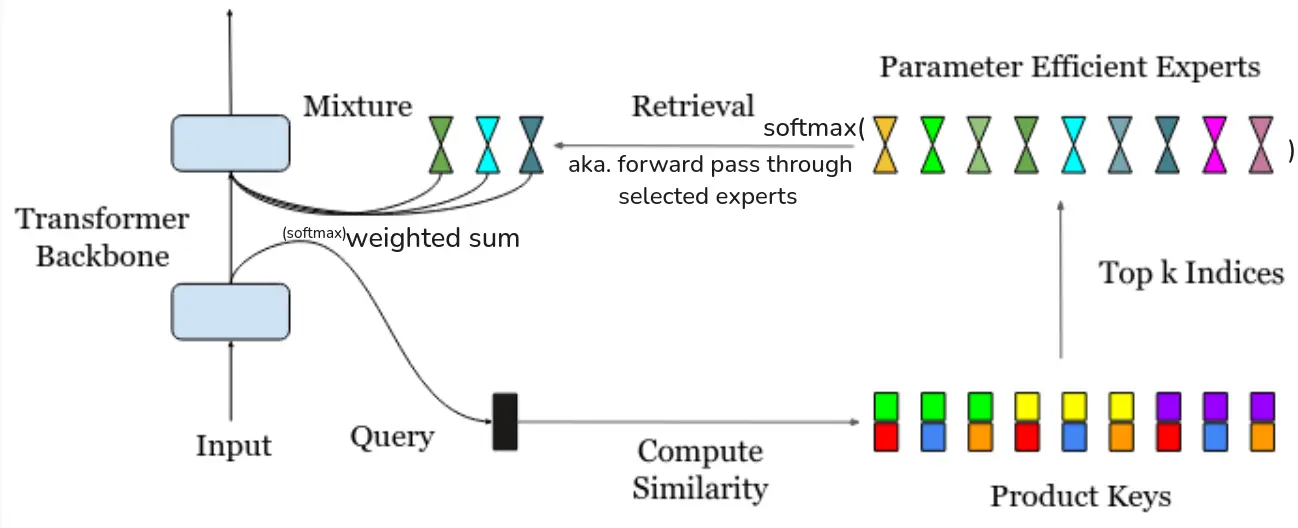
… get the top-K ${\mathcal{T}}_k$ out of $N$ experts $\mathbb{E}:=\{k_i{\}}_{i=1}^N$ by taking the dot-product between their product keys $\mathbb{K}:=\{k_i{\}}_{i=1}^N$ with the query vector $q(x)$ from the input vector $x\in {\mathbb{R}}^n$.

$$g_i(x)=\sigma (q(x{)}^T{k}_i)$$

… then take the softmax or sigmoid to those similarities, giving us the router scores (ofc we don’t recompute anything).

$$f(x)=\sum _{i\in \mathbb{I}}{g}_i(x)e_i(x)$$

… expert outputs are then aggregated via a weighted sum.

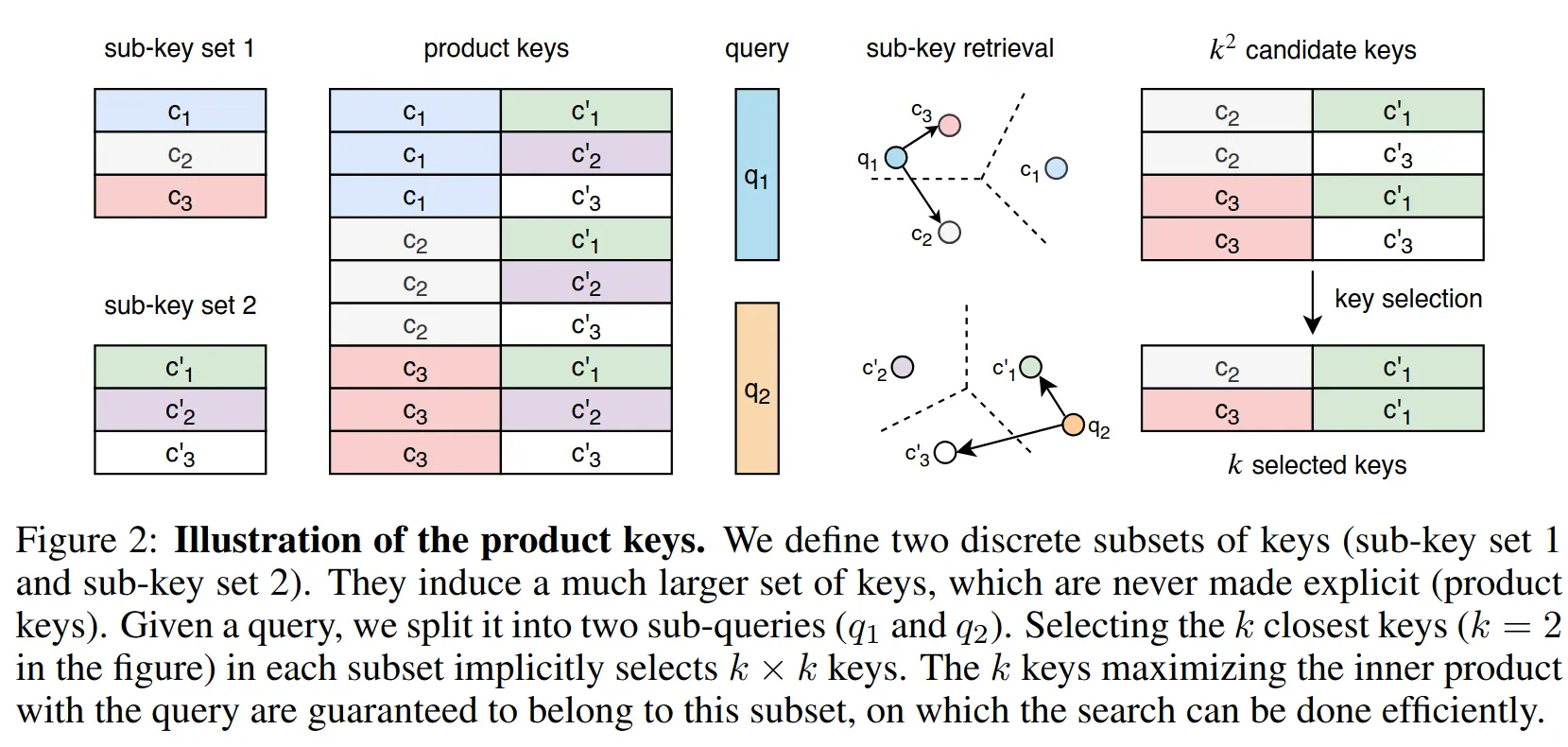
Problem: Large number of $N$ experts, each with a $d$-dim key, computing every product takes $O(Nd)$, very slow.
Solution:
We create two matrices to replace the key matrix $c\in \mathbb{C},c^{\prime }\in {\mathbb{C}}^{\prime }\subset {\mathbb{R}}^{d/2}$, which have a cardinality of $\sqrt{N}$, $c,c^{\prime }$ have dimensionality $\frac{d}{2}$.

$$\mathbb{K}=\{\left[\begin{array}{c}c\\ c^{\prime }\end{array}\right]\}$$ $${\mathbb{I}}_{\mathbb{C}}={\mathcal{T}}_k((q_1^T{c}_i)),{\mathbb{I}}_{{\mathbb{C}}^{\prime }}={\mathcal{T}}_k((q_2^T{c}_i^{\prime }))$$

where $q_1,q_2$ are the first and second half of the query vector $q(x)$. So in this equation, we are doing the dot products with halfed dimensionality and only $\sqrt{N}$ times each.
This creates $k^2$ candidate keys ${\mathbb{K}}^{\prime }:=\{\left[\begin{array}{c}{c}_i\\ c_j\end{array}\right]|i\in {\mathbb{I}}_{\mathbb{C}},j\in {\mathbb{I}}_{\mathbb{C}}^{\prime }\}$ (i.e. containing all the combinations) which contain the $k$ most similar keys from $\mathbb{K}$ to $q(x)$. We can then simply apply the top-k operator again on this set of candidates, leaving us with a runtime complexity of $O(\sqrt{N}+k^2)d$, as opposed to the original $O(Nd)$, which is much better for large $N$ - remember, $k$ is just the number of experts we choose, so way less.
This could even be done in $O(k\log (k))$ with a priority queue, but is not so GPU-friendly.

In this paper, “each expert is only a single neuron”:

$$e_i:=\sigma (u_i^T)v_i+b$$

$v_i,u_i$ are vectors with the same dim as $x$, $\sigma$ is ReLU / GELU.

???? Single neuron but the are vectors and there are two of them ???

Ig there is a single neuron for each input dimension → scalar activation output → multiplied with second vector to pull up dimensionality again (prlly $v_i$ stores information and $\sigma$ is like a gate???)

That’s prlly it - matches this figure. The “singleton” is the squashing of the input to just the scalar activation.

They increase the expressiveness of the network not by adjusting the size of the experts, but adding multiple query heads (similar to MHA / Product Key Memories), by just running them in parallel - the results get summed:

$$f(x):=\sum _{i=1}^h{f}^i(x)=\sum _{i=1}^h\sum _{j\in {\mathbb{I}}^i}{g}_j(x)e_j(x)$$

One such “PEER” layer with $h$ heads is equivalent to using one expert with $h$ hidden neurons:

$$f(x)=\sum _{i=1}^h{e}_i(x)=\sum _{i=1}^h\sigma (u_i^{T}x)v_i=V\sigma (W^{T}x)$$

where $W=\left[\begin{array}{c}{u}_1,\dots ,u_h\end{array}\right],V=\left[\begin{array}{c}{v}_1,\dots ,v_h\end{array}\right]$.
→ PEER dynamically assembles an MLP with $h$ neurons by aggregating $h$ singleton MLPs retrieved from a shared repository.
Allows sharing of hidden neurons among experts, enhancing knowledge transfer and parameter efficiency.

k