set

Prerequisites: logic

Set

A set is a collection of distinct objects, considered as an object in its own right. Sets are usually denoted by capital letters, e.g. $A,B,C$.
The objects in a set are called the elements or members of the set. We write $a\in A$ if $a$ is an element of the set $A$, and $a\notin A$ if $a$ is not an element of $A$.
$\varnothing$ denotes the empty set, which contains no elements.
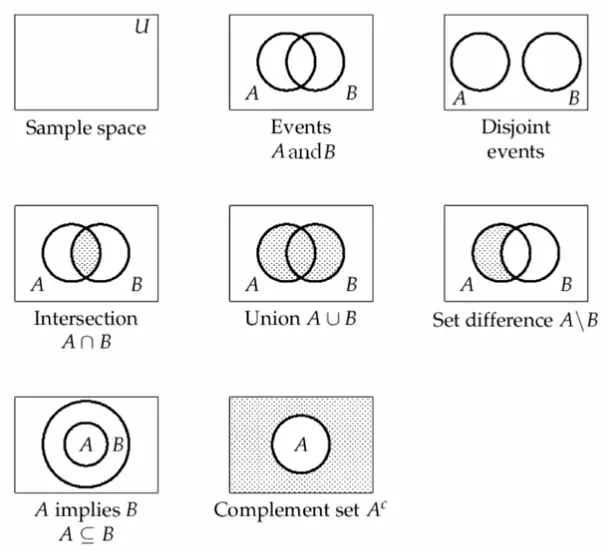
$A\subseteq$ B means that every element of $A$ is also an element of $B$.

Cardinality

The cardinality of a set $A$ is the number of elements in $A$.
We denote the cardinality of $A$ by $|A|$, also denoted by $\text{card}(A)$ or $\#A$.

Link to original

Two sets $A$ and $B$ are equal if and only if both are subsets of each other.

$$A=B⟺A\subseteq B\wedge B\subseteq A$$

Ways of denoting sets.

Roster notation: $A=\{1,2,3\}$ or $B=\{1,4,9,16,\dots \}$ listing elements (“aufzählend”)
Set builder notation: $A=\{x\mid P(x)\}$, where $P(x)$ is a property that $x$ must satisfy (“beschreibend”), e.g.: $\{1,2,3\}=\{x\mid x\in \mathbb{Z}\wedge 1\le x\le 3\}$
Subsets: $A=\{x\in E\mid Q(x)\}$ e.g.: $\{1,2,3\}=\{x\in \mathbb{Z}\mid 1\le x\le 3\}$ (more common)
Interval notation: $A=[1,3]=\{x\mid 1\le x\le 3\}$

Union (Vereinigung)

The union of two sets $A$ and $B$, denoted by $A\cup B$, is the set of all elements that are in $A$ or in $B$ or in both:

$$A\cup B=\{x\mid x\in A\vee x\in B\}$$

Or for set systems (more than two sets):

$$\bigcup _{i\in I}{A}_i=\{x\mid \exists i\in I:x\in A_i\}$$

$I$ is the index set (the set of indices for the sets which we are taking the union of).

Intersection ((Durch)Schnitt)

The intersection of two sets $A$ and $B$, denoted by $A\cap B$, is the set of all elements that are in both $A$ and $B$:

$$A\cap B=\{x\mid x\in A\wedge x\in B\}$$

Or for set systems (more than two sets):

$$\bigcap _{i\in I}{A}_i=\{x\mid \forall i\in I:x\in A_i\}$$

Complement

Let’s call $E$ the set of all elements we are working with (Grundmenge / basic set). Then we can define the complement of a set $A\subseteq E$ as the set of all elements in $E$ that are not in $A$:

$$A^{\prime }=\{x\in E\mid x\notin A\}$$

Other notations for the complement: $A^c,\overline{A}$

Difference

The difference of two sets $A$ and $B$, denoted by $A\setminus B$, is the set of all elements that are in $A$ but not in $B$:

$$A\setminus B=\{x\mid x\in A\wedge x\notin B\}$$

Symmetric difference

The symmetric difference of two sets $A$ and $B$, denoted by $A△B$, is the set of all elements that are in exactly one of the two sets (like an xor):

$$A△B=(A\setminus B)\cup (B\setminus A)=(A\cup B)\setminus (A\cap B)$$

(NOTE: Due to a bug in Obsidian-tikzjax, the symmetric difference only renders correctly in live-preview mode… click the link for correct rendering)

Properties of sets

$$\text{Satz:}\text{Seien }A,B,C\text{ und }{A}_i,i\in I,\text{ Teilmengen einer Menge }E.\text{ Dann gilt:}$$ $$\begin{array}{llllll}A\cup B& =& B\cup A,& A\cap B& =& B\cap A,\\ A\cup (B\cup C)& =& (A\cup B)\cup C,& A\cap (B\cap C)& =& (A\cap B)\cap C,\\ A\cap (B\cup C)& =& (A\cap B)\cup (A\cap C),& A\cup (B\cap C)& =& (A\cup B)\cap (A\cup C),\\ A\cap {\bigcup }_{i\in I}{A}_i& =& {\bigcup }_{i\in I}(A\cap A_i),& A\cup {\bigcap }_{i\in I}{A}_i& =& {\bigcap }_{i\in I}(A\cup A_i),\\ A\cup \varnothing & =& A,& A\cap E& =& A,\\ A\cup A^{\prime }& =& E,& A\cap A^{\prime }& =& \varnothing ,\\ A\cup A& =& A,& A\cap A& =& A,\\ A\cup E& =& E,& A\cap \varnothing & =& \varnothing ,\\ A\cup (A\cap B)& =& A,& A\cap (A\cup B)& =& A,\\ (A\cup B{)}^{\prime }& =& A^{\prime }\cap B^{\prime },& (A\cap B{)}^{\prime }& =& A^{\prime }\cup B^{\prime },\\ {\left({\bigcup }_{i\in I}{A}_i\right)}^{\prime }& =& {\bigcap }_{i\in I}{A}_i^{\prime },& {\left({\bigcap }_{i\in I}{A}_i\right)}^{\prime }& =& {\bigcup }_{i\in I}{A}_i^{\prime }.\end{array}$$

Proving set identities

“Rückführung auf logische Regeln” (reduction to logical rules):

$$A\cup B=\{x\mid x\in A\vee x\in B\}=\{x\mid x\in B\vee x\in A\}=B\cup A$$

“Anwenden der Äquivalenz” (applying the equivalence):

$$A=B⟺A\subseteq B\wedge B\subseteq A$$

Element table: Create a table with $\in$ and $\notin$ for each set, then compare the tables, just like a truth table in logic.

cartesian product

Cartesian product

The cartesian product of two sets $A$ and $B$, denoted by $A\times B$, is the set of all possible ordered pairss $(a,b)$ where $a\in A$ and $b\in B$:
$A\times B:=\{(x,y):x\in A\wedge y\in B\}$
$B\times A:=\{(y,x):x\in A\wedge y\in B\}\ne A\times B$
e.g.: $A=\{1,2,3\}$ and $B=\{a,b\}$, then $A\times B=\{(1,a),(1,b),(2,a),(2,b),(3,a),(3,b)\}$

The cartesian product is not commutative: $A\times B\ne B\times A$

Taking the cartesian product of mutiple sets:
$A_1\times A_2\times \cdots \times A_n=\{(a_1,a_2,\dots a_n)\mid \forall i:a_i\in A_i\}$

Link to original

---

Further reading:
power set
multiset
…

A note on terminology

https://mathworld.wolfram.com/Collection.html says that a collection refers to a multiset.
But gpt5 says that’s almost certainly not the case in most contexts, a collection just a set.
But collection is so generic and context dependent, I only use it as “a bunch of things” and then define if necessary, else use a more specific term.