adjacency matrix

Any graph is fully specified by its adjacency matrix.

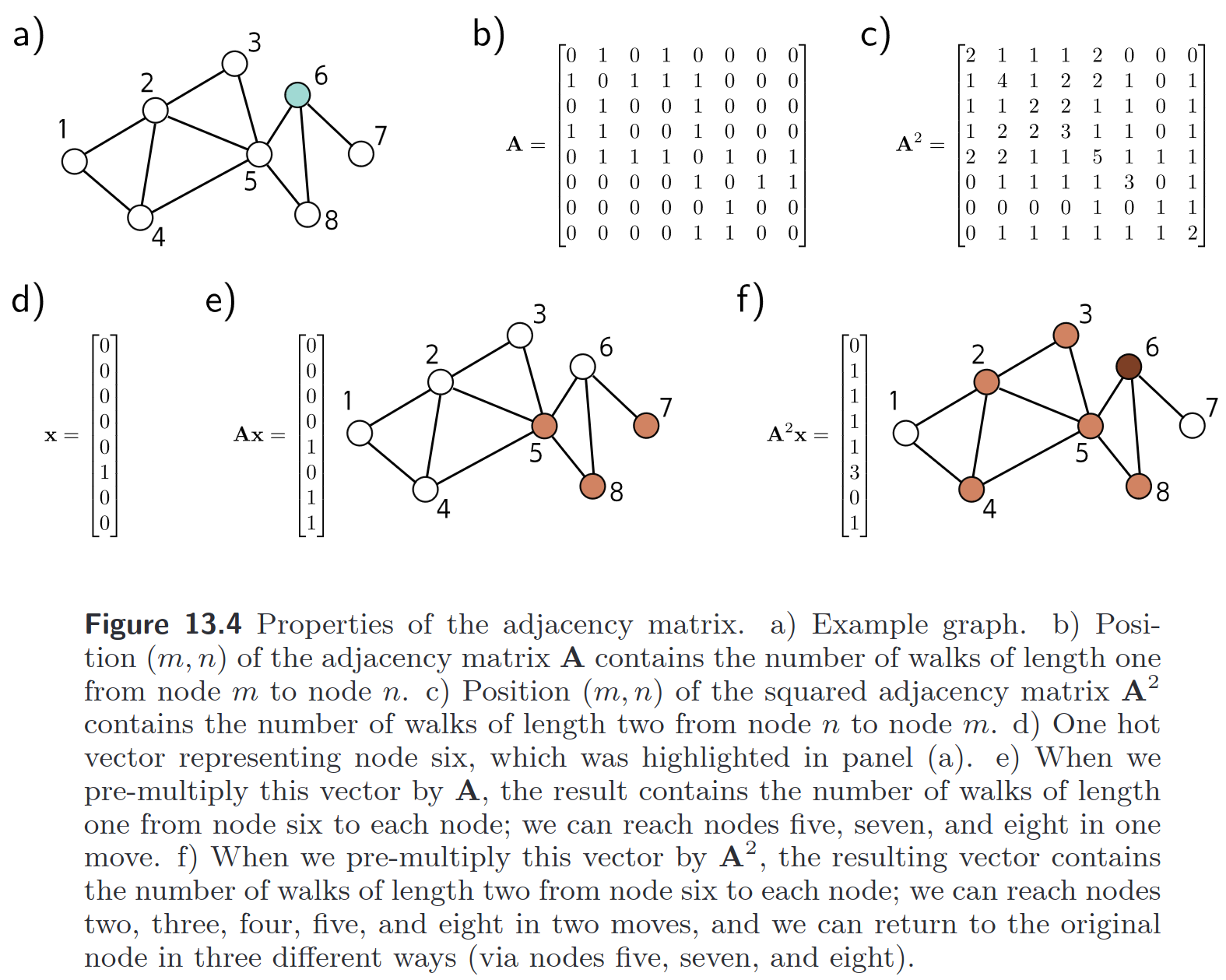
• Undirected graphs always have a symmetric adjecency matrix, the identity is all nodes having only a connection to themselves.
• All 1s in $A$ show the one-step connections to a node.
• The values on the diagonal in $A^2$ are the number of connections node $n$ has (degree).
• Other values of $A^2$ show the two-step connections node $n$ has with node $m$.

Generally: $A^L$ shows the how many $L$-step paths there are from node $n$ back to itself on the diagonal - or generally - how many paths of length $L$ from node $n$ to node $m$ (not unique; nodes can be visited multiple times, etc.). See also: matrix exponential & communicability!
A non-zero entry at position ($m$, $n$) indicates that the distance from $m$ to $n$ must be less than or equal to $L$.

Not sure what I did here… some example from the UDL book, ig.

$$\text{displaylines}\begin{array}{r}X=\left[\begin{array}{cc}{x}_{11}& x_{12}\\ x_{21}& x_{22}\\ x_{31}& x_{32}\end{array}\right],A=\left[\begin{array}{ccc}0& 1& 0\\ 1& 0& 1\\ 0& 1& 0\end{array}\right],P=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right]\\ \\ X^{\prime }=XP=\left[\begin{array}{cc}{x}_{11}& x_{12}\\ x_{21}& x_{22}\\ x_{31}& x_{32}\end{array}\right]\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right]=\left[\begin{array}{cc}{x}_{21}& x_{22}\\ x_{31}& x_{32}\\ x_{11}& x_{12}\end{array}\right]\end{array}$$ $$\text{displaylines}\begin{array}{r}{A}^{\prime }=P^{T}AP=\left[\begin{array}{ccc}0& 0& 1\\ 1& 0& 0\\ 0& 1& 0\end{array}\right]\left[\begin{array}{ccc}0& 1& 0\\ 1& 0& 1\\ 0& 1& 0\end{array}\right]\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right]=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right]\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\end{array}$$

There are many adjacency matrices that can encode the same connectivity.

This is the case when there is no natural order for the nodes, and is an issue for neural networks which are not permutation invariant.
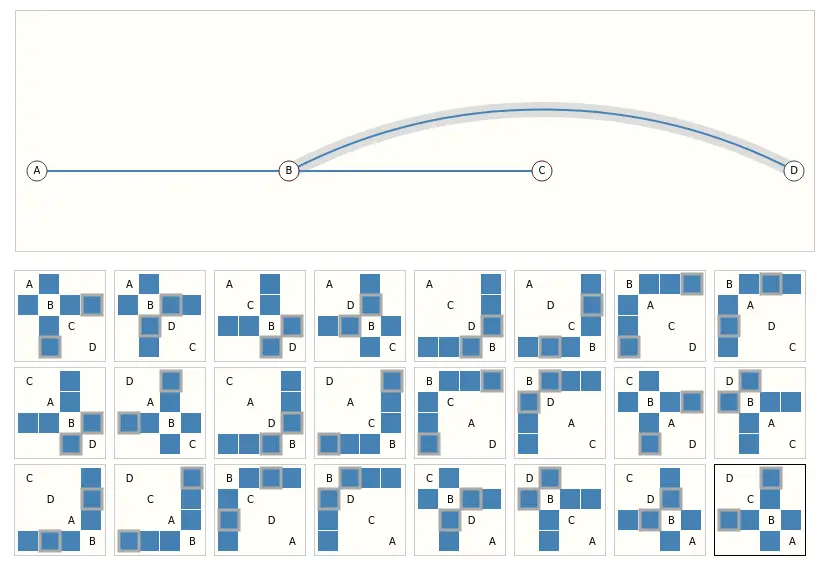
Every adjacency matrix that can describe this small graph of only 4 nodes: ($4!$)

adjacency list

Adjacency list

Adjacency matrices are usually quite sparse, wasting space and compute.
We can instead also store the graph as an adjacency list, where we store $n_{\text{edges}}$ tuples of $(i,j)$, the $k$-th entry describing the edge $e_k$ between nodes $n_i$ and $n_j$.

$$O(n_{\text{edges}})<O(n_{\text{nodes}}^2)\text{ for }{n}_{\text{edges}}<\frac{n_{\text{nodes}}^2}{2}$$

In other words, it grows with the number of existing edges rather than the number of possible edges!
This format is also permutation invariant!

Link to original

References

UDL book
https://distill.pub/2021/gnn-intro/