graph

Graph

A graph $G=(V,E)$ consists of a set of vertices $V$ and a set of edges $E$ between them. An edge $e_{ij}$ connects vertex $v_i$ with vertex $v_j$.

Terminology

An edge is incident to a vertex if it is directly connected.
Two (distinct) edges are adjacent if they share a vertex.
An induced subgraph is a subset of a graph that includes all the vertices of a given subset, along with every edge that exists between them in the original graph.
The dual of a graph is a graph where the vertices and edges are swapped. The dual contains the same information, represented differently.
In a complete graph, every pair of distinct vertices is connected by a unique edge, i.e. it’s fully connected.
A graph is homogenous if all vertices are of the same type.
If all vertices in a graph have the same degree, the graph is regular.
A cycle is a connected subgraph where every vertex has exactly two neighbours.
A k-partite graph is a graph where the vertices can be partitioned into k disjoint sets such that no two vertices in the same set are adjacent.
$a_0:=|V|$ is sometimes used as a notation for the number of vertices in a graph.
$a_1:=|E|$ is sometimes used as a notation for the number of edges in a graph.
$ϵ(G)=\frac{|E|}{|V|}$ is the density or average degree of a graph.
Simple graphs are graphs without loops or multiple edges between the same vertices.
Adjacency means two vertices are connected by an edge.
Incidence means a vertex is connected to an edge.

Transclude of reachable

Transclude of connected

Transclude of strongly-connected#^d42a8d

https://www.dmg.tuwien.ac.at/gittenberger/Folien/GrTh_u_NW.pdf

Graphs are Matrices

Graph paper reading list

Nice visualization tool: https://csacademy.com/app/graph_editor/

multigraph, hierarchical graph:

---

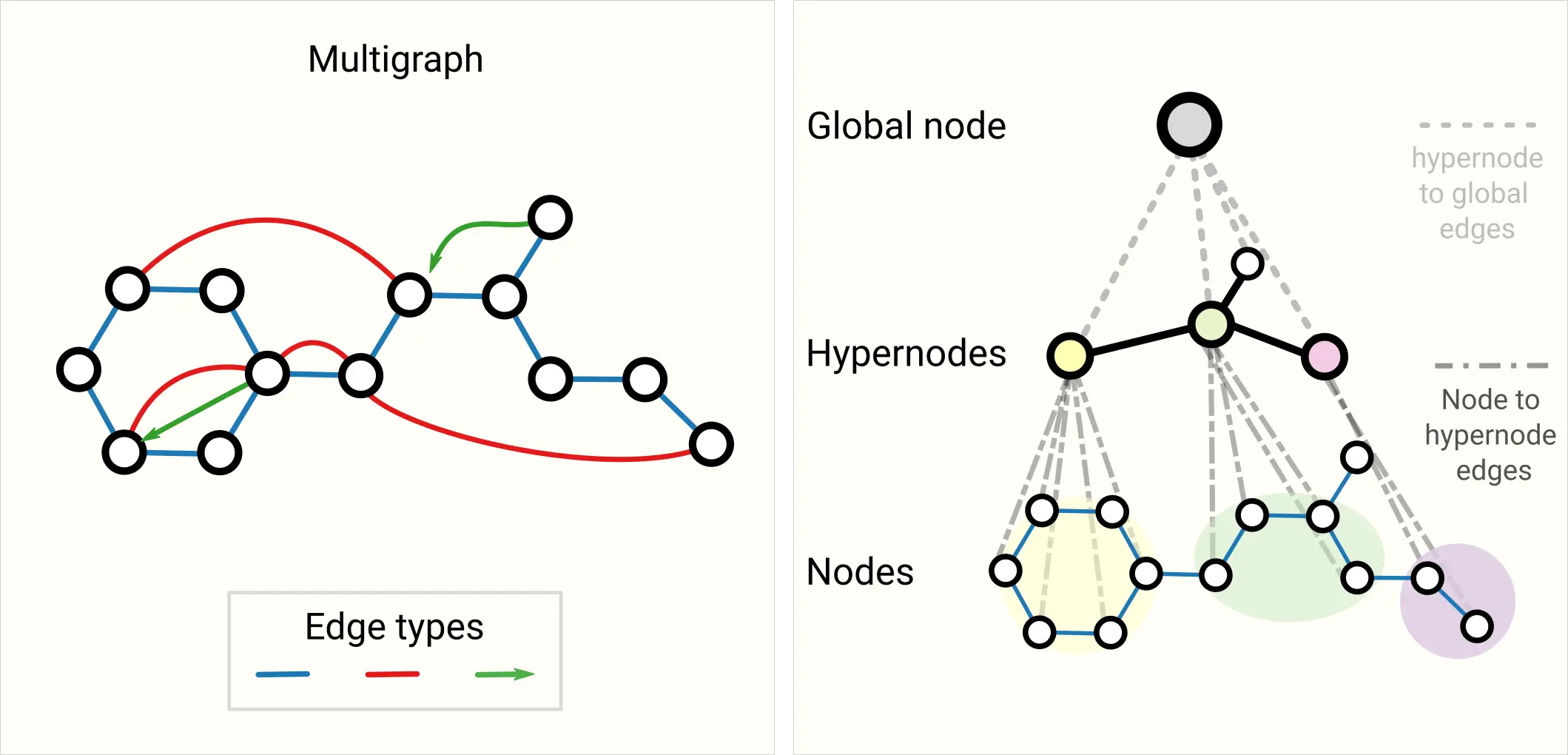
Some basic graph notes:

Neighbourhood of a vertex

The neighbourhood $N_i$ of a vertex $v_i$ in a graph is defined as its immediately connected neighbours:

$$N_i=\{v_j:e_{ij}\in E\vee e_{ji}\in E\}$$

Read: ”The neighbourhood $N_i$ of vertex $v_i$ is the set of all vertices $v_j$, such that there is an edge $e_{ij}$ from $v_i$ to $v_j$ in the set of edges $E$ or there is an edge $e_{ji}$ from $v_j$ to $v_i$ in the set of edges $E$.” (for undirected graphs, $e_{ij}=e_{ji}$)
Sometimes this is denoted as $\Gamma (v)$.
The number of verticies in the neighbourhood is called the degree.

When $v_i$ itself is not part of the neighbourhod, we call it the open neighbourhood (default). If it is, then we call it the closed neighbourhood, denoted by $N_G[v]$ (as opposed to $N_G(v)$).

Link to original

Transclude of triplet

Transclude of triangle#^9c96d8

clustering coefficient