bias refers to the error introduced by approximating a real-world problem with a simplified model. A high-bias model makes strong assumptions about the data and tends to underfit - it’s too simple to capture the underlying patterns. Think of a linear regression trying to fit clearly non-linear data.
variance refers to how much the model’s predictions would change if we trained it on different training data. A high-variance model is very sensitive to the training data and tends to overfit - it learns the noise in the training data rather than the true underlying patterns. Think of a complex polynomial that perfectly fits every training point but wildly oscillates between them.
In a nutshell
→ As we make our model more complex (reducing bias), it becomes more sensitive to the training data (increasing variance).
→ As we make our model simpler (reducing variance), it makes stronger assumptions (increasing bias).
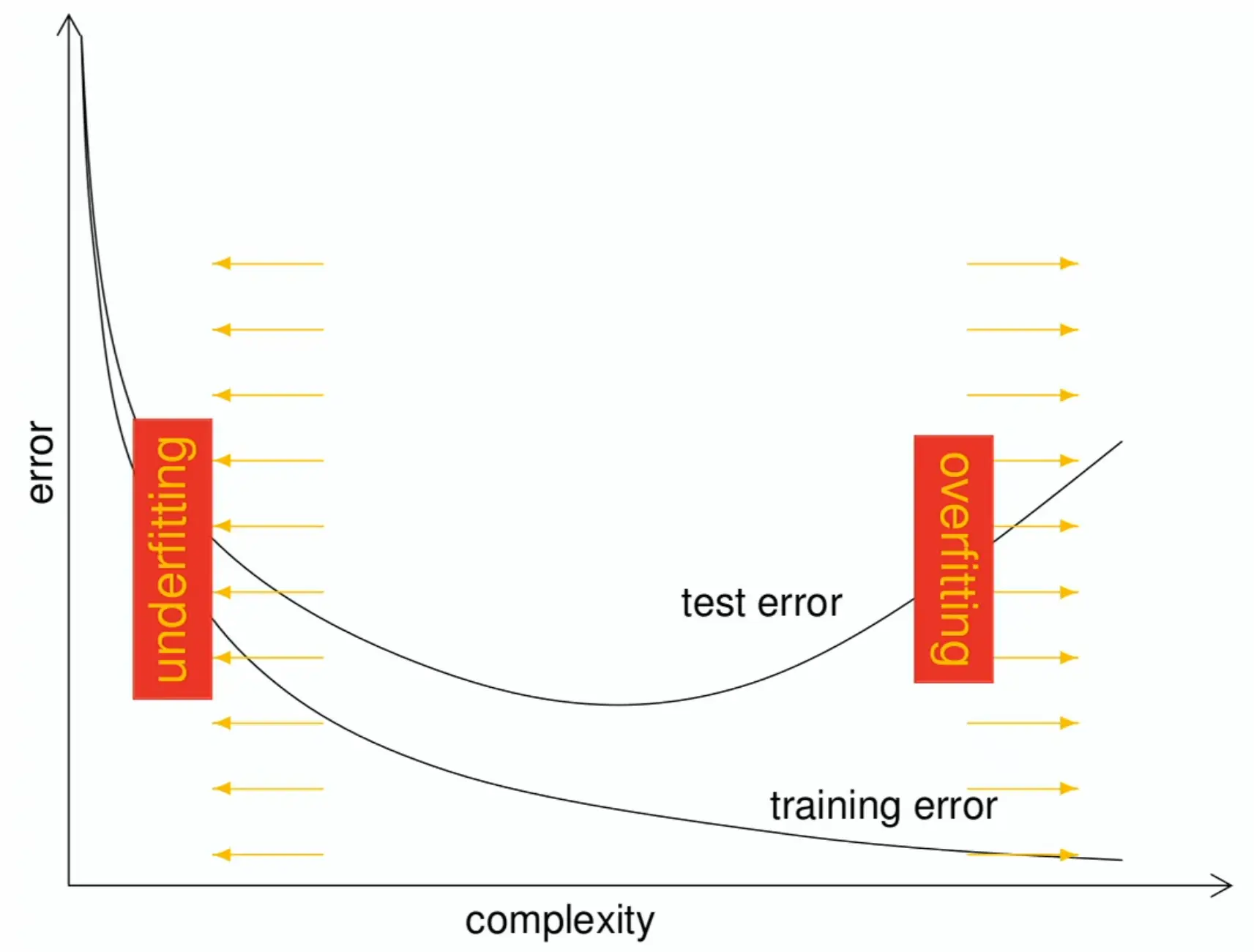
The bias-variance tradeoff in supervised learning
If we train plain empirical risk minimization (ERM), we run the risk of overfitting, where the model fits the training data well (low empirical risk) but performs poorly on unseen data (high generalization error), aka high variance.
→ Assume data samples are iid and partition data into training and validation/test sets to estimate generalization error, e.g. using cross-validation. Validation sets for hyperparameter tuning, to avoid data overlaps/leakage.
→ Use regularization techniques (like L2 regularization, dropout, data augmentation) to reduce overfitting and improve generalization.
The sweetspot is where train and test errors align.
“model” can also refer to different things, like a reward function:
Bias variance tradeoff in policy optimization
→ Using actual returns (vanilla policy gradient) gives high variance because returns depend on many random events (and timing / credit assignment is unclear), but no bias because we’re using real data.
→ Using a value function (like actor critic) reduces variance because we’re using a simpler, more stable estimate, but introduces bias because our value function doesn’t match to the true returns.
→ While variance is annoying as it makes your training potentially unstable and requires more examples to train on, bias can be a bigger problem, as you model might learn the wrong thing, and even with infinite samples never find the optimal policy (fail to converge, or converge to a suboptimal solution).