cumulative distribution function

Cumulative Distribution Function (CDF)

The cumulative distribution function (CDF) of a random variable $X$ is a function that gives the probability that $X$ will take a value less than or equal to $x$. It is defined as:

$$\begin{array}{rl}{F}_X(x)& =P(X\le x)={\int }_{-\infty }^x{f}_X(t)dt\end{array}$$

where $f_X(t)$ is the probability density function (PDF) of $X$.

standard normal distribution CDF ($\Phi$)

For the standard normal distribution ($\mu =0,\sigma =1$), the CDF is often denoted as $\Phi (x)$.

For the interval $[-1,1]$, which represents 1 standard deviation from the mean:

$$P(-1\le X\le 1)=\Phi (1)-\Phi (-1)\approx 0.8413-0.1587=0.6826$$

This shows that approximately 68% of values drawn from a standard normal distribution lie within one standard deviation of the mean.

The CDF is a non-decreasing function with a range of $[0,1]$

For any real-valued random variable, the CDF has the following properties:

• ${\lim }_{x\to -\infty }{F}_X(x)=0$
• ${\lim }_{x\to \infty }{F}_X(x)=1$
• $F_X(x)$ is non-decreasing (i.e., $F_X(a)\le F_X(b)$ for all $a\le b$)

Relationship between PDF and CDF

The PDF is the derivative of the CDF (when the derivative exists):

$$f_X(x)=\frac{d}{dx}{F}_X(x)$$

Conversely, the CDF is the integral of the PDF:

$$F_X(x)={\int }_{-\infty }^x{f}_X(t)dt$$

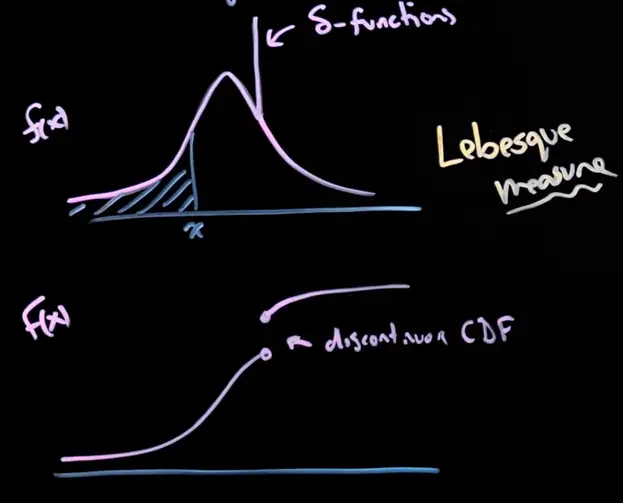
CDFs are often nicer to work with than PDFs for discontinuous distributions

For PDFs, you’d need ugly delta functions to represent jumps, which are nicer to work with if integrated over.
Another approach is lebesgue integration, which is more general than riemann integration and can handle discontinuities better.