standard normal distribution

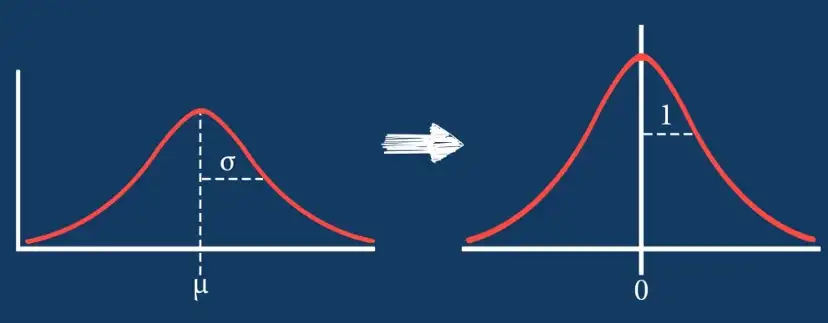
A standard normal distribution is a normal distribution with a mean $\mu =0$ and unit standard deviation $\sigma =1$.

standard normal distribution CDF ($\Phi$)

For the standard normal distribution ($\mu =0,\sigma =1$), the CDF is often denoted as $\Phi (x)$.

For the interval $[-1,1]$, which represents 1 standard deviation from the mean:

$$P(-1\le X\le 1)=\Phi (1)-\Phi (-1)\approx 0.8413-0.1587=0.6826$$

This shows that approximately 68% of values drawn from a standard normal distribution lie within one standard deviation of the mean.

Link to original

Isotropic gaussians are rotation invariant around their mean. E.g. standard normal distribution: If $X\sim \mathcal{N}(0,I)$ and $Q$ is an orthogonal matrix, then $QX\sim \mathcal{N}(0,I)$.

Link to original

Standard normal distribution is an isotropic gaussian

Let $f_X(x)=\frac{1}{\sqrt{2\pi }}{e}^{-x^2/2}$ and $f_Y(y)=\frac{1}{\sqrt{2\pi }}{e}^{-y^2/2}$ be two independent standard normal distributions.
Then the joint distribution $f_{X,Y}(x,y)=f_X(x)f_Y(y)$ is an isotropic gaussian:

$$f_{X,Y}(x,y)=\frac{1}{2\pi }{e}^{-(x^2+y^2)/2}$$

$(x^2+y^2)$ is the squared distance from the origin, so the density is constant on circles around the origin.

Link to original