random variable

A random process, where each outcome is associated with some number.

Random Variable

A random variable $X$ is a function that maps outcomes from a probability space to real numbers.
Formally, $X:\Omega \to \mathbb{R}$ where $\Omega$ is the sample space.

Technical requirement: For any Borel set $B\subseteq \mathbb{R}$, the preimage $X^{-1}(B)=\{\omega \in \Omega :X(\omega )\in B\}$ must be measurable (i.e., it must be an event we can assign probability to).

Types of Random Variables

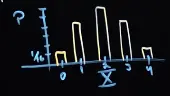
discrete: Takes countably many values (e.g., coin flips, die rolls)

• Has a probability mass function (PMF): $P(X=x)$
• CDF is a step function

continuous: Takes any value in an interval (e.g., height, temperature)

• Has a probability density function (PDF): $f_X(x)$
• CDF is continuous: $F_X(x)=P(X\le x)={\int }_{-\infty }^x{f}_X(t)dt$

Rolling a fair six-sided die

$\Omega =\{\text{face1},\text{face2},\text{face3},\text{face4},\text{face5},\text{face6}\}$
$X:\Omega \to \{1,2,3,4,5,6\}$ maps each face to its number

Each outcome has probability $P(X=k)=\frac{1}{6}$ for $k\in \{1,2,3,4,5,6\}$ (uniform distribution)

expected value: $E[X]={\sum }_{k=1}^{6}k\cdot P(X=k)=\frac{1}{6}(1+2+3+4+5+6)=3.5$

Flipping a coin 4 times and counting the number of heads:

The sample space $\Omega$ contains all $2^4$ possible sequences of 4 flips $\{HHHH,HHHT,\dots ,TTTT\}$.
Let $X$ be the random variable counting the number of heads.
For $X\in \{0,1,2,3,4\}$, the probability distribution is:

$$\begin{array}{rl}P(X=0)& =1/16\text{(TTTT)}\\ P(X=1)& =4/16\text{(HTTT, THTT, TTHT, TTTH)}\\ P(X=2)& =6/16\text{(HHTT, HTHT, HTTH, THHT, THTH, TTTH)}\\ P(X=3)& =4/16\text{(HHHT, HHTH, HTHH, THHH)}\\ P(X=4)& =1/16\text{(HHHH)}\end{array}$$

This follows a binomial distribution with $n=4$ trials and probability $p=1/2$ of heads on each trial.

Random variables are a concise summary of probabilitiies / useful abstractions…

They let us:

• Apply functions and transformations
  • e.g. the probability function → probability distribution.
  • Calculate expected value, variance, standard deviation
  • Answer practical questions like “What’s the probability of getting 10-15 emails in the next hour?”
  • what’s the probability of being in a range of values?
  • what value do I expect, if I just sample a random item?
  • how much spread does the distribution have?
  • how surprised would I be if the sampled item differs by so much?
  • how many emails do I expect to get in the next 10 minutes, given a certain rate of email?
  • would I be surprised if I got no emails in that time?

Two random variables can be independent, meaning the outcome of one does not affect the probability distribution of the other.

$X$ and $Y$ are independent if:

$$P(X\in A,Y\in B)=P(X\in A)P(Y\in B)$$

for all Borel sets $A,B\subseteq \mathbb{R}$. For discrete random variables, this simplifies to $P(X=a,Y=b)=P(X=a)P(Y=b)$ for all possible values $a,b$.

Functions of Random Variables

If $X$ is a random variable and $g:\mathbb{R}\to \mathbb{R}$, then $Y=g(X)$ is also a random variable.

Notatio:
$X\dots Y=g(X)$
PDF: $f_X$
CDF: $F_X=P(X<x)={\int }_{-\infty }^x{f}_X(x)dx$
We can go from $F_X\underset{g}{\to }{F}_Y$ directly, and then from $F_Y$ to $f_Y$. by taking the derivative, but we can’t go from $f_X$ to $f_Y$ directly
why?
Example: Mapping distribution of probability in C to F: $X\sim \mathcal{N}(\mu ,{\sigma }^2)⟹Y=aX+b$
If you just do it naively like that the result might no longer be a normal / probability distribution.

Finding the distribution of $Y=g(X)$

Method 1: Through CDFs (always works)
$F_Y(y)=P(Y\le y)=P(g(X)\le y)=P(X\le g^{-1}(y))=F_X(g^{-1}(y))$
Then differentiate to get $f_Y(y)=\frac{d}{dy}{F}_Y(y)$

Method 2: Direct PDF transformation (when $g$ is monotonic)

$$f_Y(y)=f_X(g^{-1}(y))\cdot \left|\frac{d}{dy}{g}^{-1}(y)\right|$$

The derivative term (Jacobian) accounts for how $g$ stretches/compresses probability density.

Standardizing a normal distribution

Given $X\sim \mathcal{N}(\mu ,{\sigma }^2)$, we want $Y=\frac{X-\mu }{\sigma }\sim \mathcal{N}(0,1)$

Using Method 1:

$$F_Y(y)=P\left(\frac{X-\mu }{\sigma }\le y\right)=P(X\le \sigma y+\mu )=F_X(\sigma y+\mu )$$

Differentiating:

$$f_Y(y)=f_X(\sigma y+\mu )\cdot \sigma =\frac{1}{\cancel{\sigma }\sqrt{2\pi }}{e}^{-\frac{(\sigma y+\cancel{\mu }-\cancel{\mu }{)}^2}{2{\sigma }^2}}\cdot \cancel{\sigma }=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{y^2}{2}}$$

This is the standard normal PDF, confirming $Y\sim \mathcal{N}(0,1)$.