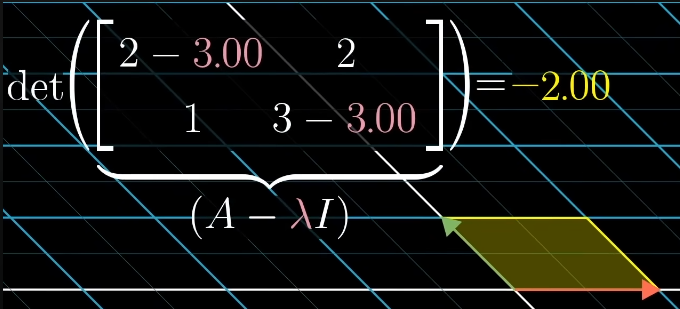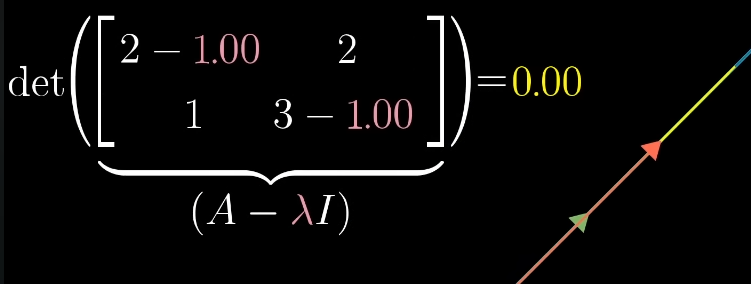eigenvalue

Eigenvectors are vectors who’s span is unchanged by a linear transformation.

Eigenvectors only get stretched/squished (scaled) or are left unchanged.
The eigenvalue $\lambda$ is the value by which the vector is scaled.
You can think of it as the axis of rotation.
For a true rotation however, the eigenvalue needs to be $\pm 1$, as rotations don’t scale vectors (we call those transformation matrices unitary)

Applying the transformation matrix $A$ to the eigenvector $\vec{v}$ is equivalent to simply scaling it by its eigenvalue $\lambda$:

$$A\vec{v}=\lambda \vec{v}$$

We want to figure out the eigenvector $\vec{v}$ and the eigenvalue $\lambda$:
For that we make both sides look like matrix-vector multiplication, by multiplying $\lambda$ with the identity.

$$A\vec{v}=(\lambda I)\vec{v}$$

We now want the nonzero solution for $\vec{v}$:

$$\begin{array}{rl}A\vec{v}-(\lambda I)\vec{v}& =\vec{0}\\ (A-\lambda I)\vec{v}& =\vec{0}\end{array}$$

The product of a nonzero vector with a nonzero matrix can only be zero if the determinant is zero, so we are looking for a $\lambda$ that satisfies: $\det (A-\lambda I)=0$
Meaning we tweak lambda in such a way, that the resulting transformation squishes space to a lower dimension:

If $\det (A\vec{v})=0$, then the transformation changes the space in a way that it collapses to a lower dimension (for the case of ${\mathbb{R}}^3$ it may be a plane, line or point: anything with 0 volume).

Link to original

So we need to solve the equation $\det (A-\lambda I)=0$ for $\lambda$, then we can find the eigenvector $\vec{v}$, which stays on its span, scaled by $\lambda$, by solving the equation $(A-\lambda I)\vec{v}=\vec{0}$.

Not every transformation has a real eigenvector.

A $90°$ rotation e.g.

$$\begin{array}{rl}\det \left(\left[\begin{array}{cc}-\lambda & -1\\ 1& -\lambda \end{array}\right]\right)& =(-\lambda \cdot -\lambda )-(-1\cdot 1)={\lambda }^2+1=0\\ & \to \lambda =i\text{ or }\lambda =-i\end{array}$$

only has the imaginary eigenvectors $i$ and $-i$:
The axis of rotation is around the complex plane, at the origin.
So multiplying with $i$ usually means some kind of rotation. This is also the case within the complex plane (the angles get added together).

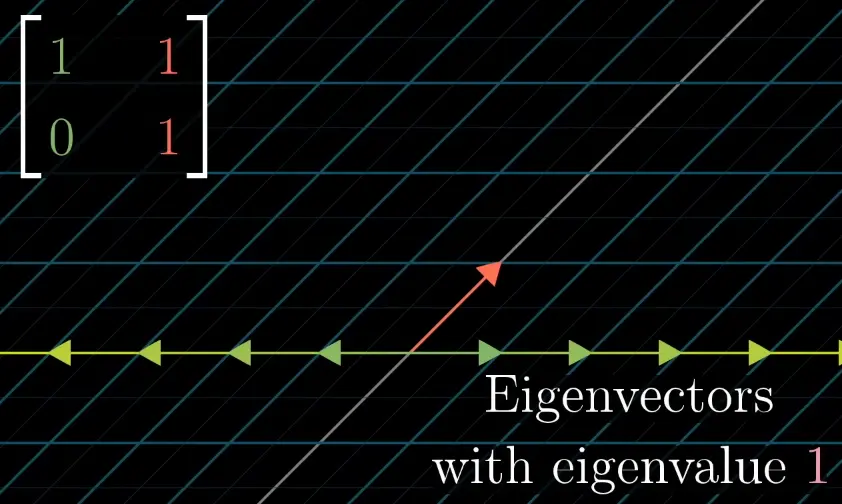
A shear like $\left[\begin{array}{cc}1& 1\\ 0& 1\end{array}\right]$ only has a single eigenvalue.

$$\begin{array}{rl}& \det \left(\left[\begin{array}{cc}1-\lambda & 1\\ 0& 1-\lambda \end{array}\right]\right)=(1-\lambda )\cdot (1-\lambda )=0\\ & \to \lambda =1\end{array}$$

The eigenspace is 1-dimensional … a single eigenline:

In a diagonal matrix, all vectors are eigenvectors, and the diagonal entries are the eigenvalues.

Diagonal matrices only scale what they are being multiplied with, since the basis vectors are also eigenvectors. For diagonal matrices, every vector is an eigenvector.

The matrix $\left[\begin{array}{cc}2& 0\\ 0& 2\end{array}\right]$ scales every vector by 2. Every vector is an eigenvector with $\lambda =2$.

Diagonal matrices have nice computational properties when taking large powers.

$${\left[\begin{array}{cc}a& 0\\ 0& b\end{array}\right]}^k\cdot \left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{cc}{a}^{100}& 0\\ 0& b^{100}\end{array}\right]\cdot \left[\begin{array}{c}x\\ y\end{array}\right]$$

Link to original

Transclude of diagonal-matrix#^90bb0f

Eigenvector puzzle

3b1b’s solution: Eigenvalue puzzle solution.pdf

Highlights from the solution / my take:

$$\begin{array}{rl}A& =\left[\begin{array}{cc}0& 1\\ 1& 1\end{array}\right]\\ A^2& =\left[\begin{array}{cc}1& 1\\ 1& 2\end{array}\right]\\ A^3& =\left[\begin{array}{cc}1& 2\\ 2& 3\end{array}\right]\\ A^4& =\left[\begin{array}{cc}2& 5\\ 5& 8\end{array}\right]\\ A^5& =\left[\begin{array}{cc}5& 7\\ 7& 13\end{array}\right]\end{array}$$

The terms form the fibonacci sequence:

$$\left[\begin{array}{cc}0& 1\\ 1& 1\end{array}\right]\left[\begin{array}{c}a\\ b\end{array}\right]=\left[\begin{array}{c}b\\ a+b\end{array}\right]$$

The eigenvalues of $A$ were computed by:

$$\begin{array}{rl}& \det ([A-\lambda I])=\det \left(\left[\begin{array}{cc}0-\lambda & 1\\ 1& 1-\lambda \end{array}\right]\right)={\lambda }^2-\lambda -1=0\\ & \to {\lambda }_{1,2}=\frac{1\pm \sqrt{5}}{2}\end{array}$$

… ${\lambda }_1$ is the golden ratio $\varphi =1.618\dots$, and ${\lambda }_2$ is $-\frac{1}{\varphi }=-0.618\dots$.

(after calculating the eigenvectors …)

Converting to the eigenbasis:

$$\begin{array}{rl}D& =S^{-1}AS\\ & ={\left[\begin{array}{cc}2& 2\\ 1+\sqrt{5}& 1-\sqrt{5}\end{array}\right]}^{-1}\left[\begin{array}{cc}0& 1\\ 1& 1\end{array}\right]\left[\begin{array}{cc}2& 2\\ 1+\sqrt{5}& 1-\sqrt{5}\end{array}\right]\\ & ⋮\\ & =\left[\begin{array}{cc}{\lambda }_1& 0\\ 0& {\lambda }_2\end{array}\right]\end{array}$$

Now we can compute:

$$D^n=\left[\begin{array}{cc}{\lambda }_1^n& 0\\ 0& {\lambda }_2^n\end{array}\right]$$

…instead of tedious matrix multiplication.

To translate back into the original cordinate system: $A^n=S(D^n)S^{-1}$

Okay I’m not typing this shit, looks sick tho (look at the solution pdf for the equation).
It’s a really interesting / funny way of computing fibonacci.
(And ig probably the most efficient? As you don’t need any recursion)

References

vector

3b1b: Eigenvectors and eigenvalues | Chapter 14, Essence of linear algebra

https://www.khanacademy.org/math/linear-algebra/alternate-bases/eigen-everything/v/linear-algebra-introduction-to-eigenvalues-and-eigenvectors