determinant

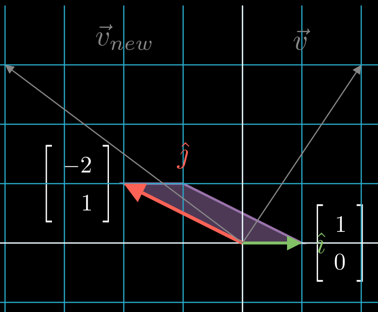
Notation: $det(A)=|A|$

TLDR:

• A square matrix $A$ is invertible $⟺$ its determinant is non-zero $⟺$ its rank is full (equals its size $n$).
• It is the product of its eigenvalues (If $A$ is a diagonal matrix, its determinant is $\prod \mathrm{diag}(A)$).
• This tells us how volume in $n$-dimensional space changes when transformed by the matrix.
• Defined only for square matrices because only they map $n$-dimensional space to itself.

Determinant

Properties 4-10 are derived from the first three, which form the basis of the determinant definition.

1] $\det (I)=1$

2] Exchanging two rows changes the sign of the determinant
→The determinant of a permutation matrix is $+1$ if the number of row exchanges is even, else $-1$.

3a] $\left|\begin{array}{cc}ta& tb\\ c& d\end{array}\right|=t\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|$ … multiplying a row by a scalar is the same as multiplying the entire determinant by that scalar.
→ The determinant behaves like volume: $\det (2A)=2^n\det (A)$.
3b] $\left|\begin{array}{cc}a+a^{\prime }& b+b^{\prime }\\ c& d\end{array}\right|=\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|+\left|\begin{array}{cc}{a}^{\prime }& b^{\prime }\\ c& d\end{array}\right|$ … determinants are column.
Note: $\det (A+B)\ne \det (A)+\det (B)$)

4] Two equal rows → $\det =0$
By property 2, if the sign changes but the matrix is the same, the determinant must be zero.
Confirmed by the fact that the rank of the matrix is less than it’s size $n$.

5] Subtracting a multiple of one row from another does not change the determinant.

$$\left|\begin{array}{cc}a& b\\ c-\lambda a& d-\lambda b\end{array}\right|\stackrel{(3b)}{=}\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|+\left|\begin{array}{cc}a& b\\ -\lambda a& -\lambda b\end{array}\right|\stackrel{(3a)}{=}\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|-\lambda \left|\begin{array}{cc}a& b\\ a& b\end{array}\right|\stackrel{(4)}{=}0$$

6] Row of zeros → $\det (A)=0$

$$\left|\begin{array}{cc}0\cdot a& 0\cdot b\\ c& d\end{array}\right|\stackrel{(3a)}{=}0\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|$$

7]

$$\text{Let }U=\left|\begin{array}{cccc}{d}_1& \ast & \ast & \ast \\ 0& d_2& \ast & \ast \\ 0& 0& \ddots & \ast \\ 0& 0& 0& d_n\end{array}\right|=(d_1,d_2,\dots ,d_n)$$

… the determinant of a triangular matrix is the product of its pivots.
We can simply eliminate the stars by multiplying the rows with the corresponding $d_i$. This leaves us with a diagonal matrix. By rule 3a) we can pull out the $d_i$ from the determinant, leaving us with the product of the pivots times $\det (I)=1$ (property 1). You need to keep track of row exchanges made (property 2).
→ So the algorithm for finding the determinant, when $A$ is invertible is $A\to U\to D\to d_1{d}_2\dots d_n$.
For a $2\times 2$ matrix: $\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|\to \left|\begin{array}{cc}a& b\\ 0& d-\frac{c}{a}b\end{array}\right|=ad-bc$
→ If $a$ is $0$, we can exchange rows (property 2) first, if $c$ is also $0$, then the determinant is $0$ (property 6).
8] $\det (A)=0$ iff $A$ is singular (not invertible).
The determinant is zero if one of the $d_i$ is zero, which means we can construct a row of zeros → not linearly independent.
9] $\det (AB)=\det (A)\det (B)$
For diagonal matrices it’s easy to see why:
$\det (A)=a_1{a}_2\cdots a_n,\det (B)=b_1{b}_2\cdots b_n,\det (AB)=(a_1{b}_1)(a_2{b}_2)\cdots (a_n{b}_n)=\det (A)\det (B)$.

This tells us how we can calculate $\det (A^{-1})$:
$\det (A^{-1})\det (A)=\det (A^{-1}A)=\det (I)=1⟹\det (A^{-1})=\frac{1}{\det (A)}$
Which, again, is easy to see for diagonal matrices: $\det (A)=a_1{a}_2\cdots a_n$, $\det (A^{-1})=\frac{1}{a_1}\cdot \frac{1}{a_2}\cdots \frac{1}{a_n}=\frac{1}{\det (A)}$.

What’s more, it shows us that:
$\det (A^n)=\det (A{)}^n$, and
$\det (2A)=2^n\det (A),A\in {\mathbb{R}}^{n\times n}$ … from 3a … behaves like volume!

10] $\det (A^T)=\det (A)$
There is nothing special about “row1”, because we can exchange rows (property 2) and there is nothing special about rows in general, because we can exchange rows for columns.
The proof for 10) is also about bringing the matrices into triangular forms (1s on the diagonal).

Visual Intuition.

The absolute value of the determinant is the Area/Volume/… in ${\mathbb{R}}^2/{\mathbb{R}}^3$/… etc after the transformation described by the matrix has taken place on the unit square/cube/… etc.

It is easiest to grasp the changes of a matrix multiplied with another matrix / set of vectors does, by visualizing how it transforms the unit vectors of of the vector space:

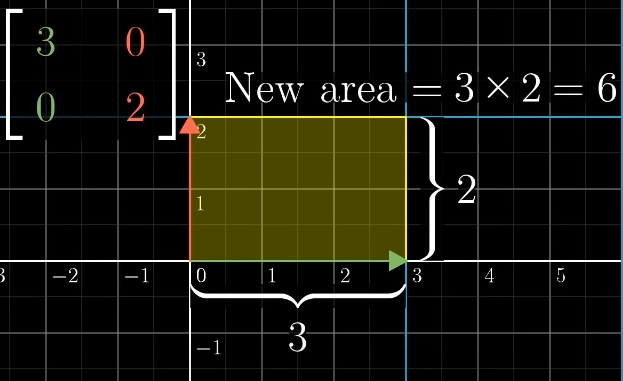
The matrix $A=\left[\begin{array}{ccc}3& & 0\\ 0& & 2\end{array}\right]$ multiplies $\hat{i}$ by 2 and $\hat{j}$ by 3, scaling the area of the unit square by $\det (A)=6$:

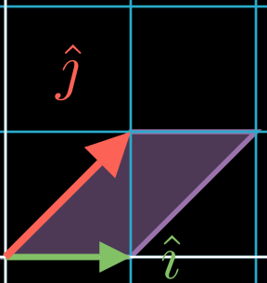
A shear matrix like $A=\left[\begin{array}{ccc}1& & 1\\ 0& & 1\end{array}\right]$ tilts the coordinate system and the unit square into a paralellogram.
For this particular $A$, the Area of the resulting parallelogram will stay the same
($P_x\cdot P_h=1\cdot 1=1$):

The determinant tells us how every area on the entire space changes in size.
The elements of the transformation matrix tell us about the shape. As we are dealing with linear transformations, the grid lines always remain parallel and evenly spaced.

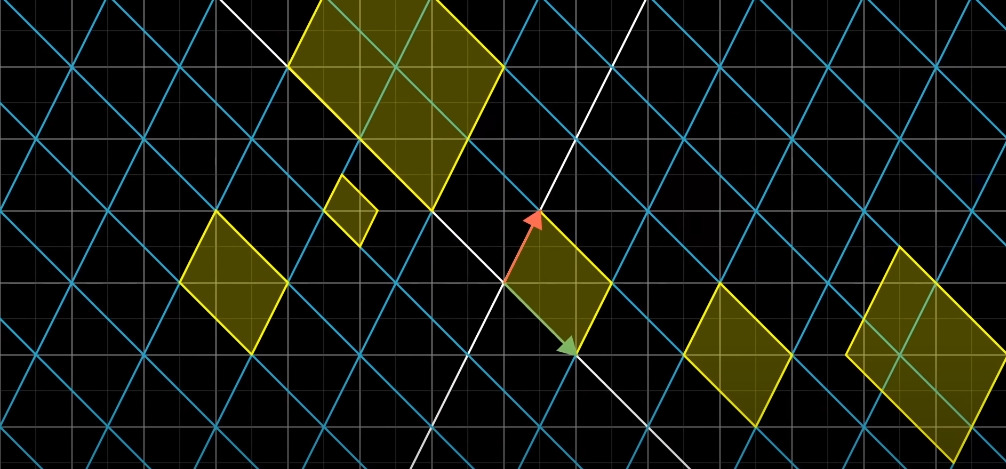
If $\det (A\vec{v})=0$, then the transformation changes the space in a way that it collapses to a lower dimension (for the case of ${\mathbb{R}}^3$ it may be a plane, line or point: anything with 0 volume).

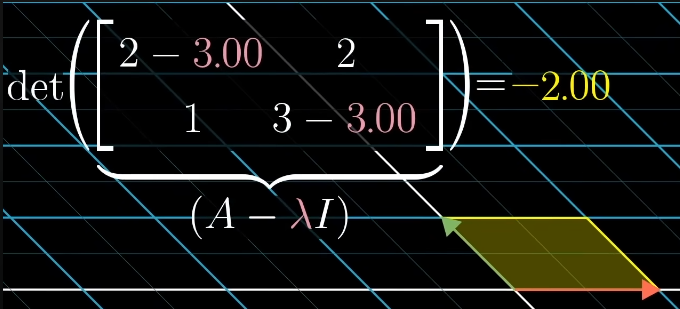
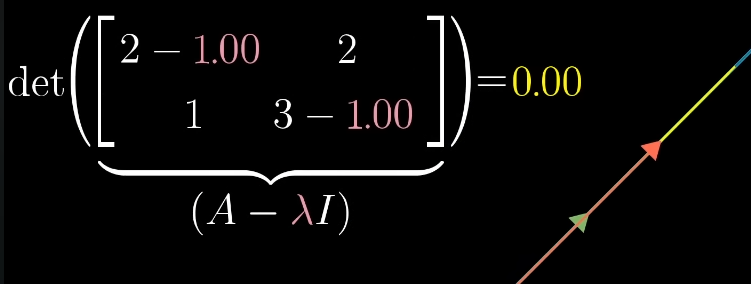
Negative elements mean that the positions of $\hat{i}$ and $\hat{j}$ have been switched.
$A=\left[\begin{array}{ccc}-2& & 0\\ 0& & 1\end{array}\right]$ for example puts $\hat{i}$ to the left and multiplies it by two. The resulting determinant/area will be $-2$:

---

Computation.

Elimination gaussian elimination to obtain a triangular matrix. The product of its pivots is the determinant.

We can use

If you interchange (swap positions) of two rows, you need to multiply the resulting determinant by $-1$.
So for an even number of swaps, the sign stays the same.

For $2\times 2$ matrices:

$$\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|\to \left|\begin{array}{cc}a& b\\ 0& d-\frac{c}{a}b\end{array}\right|=ad-bc$$

Intuition:
$a$ scales $\hat{i}$, $d$ scales $\hat{j}$. Multiplying them gives the area of the bigger / smaller rectangle.
If $b$ or $c$ is $0$, we have a parallelogram, still with area $ad$. (If only $b$ or $c$ changes in general, the paralellogram gets more / less stretched out, but area stays $1$.

Squished rectangle / parallelogram:

$$\begin{gathered} A=\left[\begin{array}{cc}1& -2\\ 0& 1\end{array}\right] \\ \vec{v}=\left[\begin{array}{c}2\\ 3\end{array}\right] \\ {\vec{v}}_{new}=A\vec{v}=\left[\begin{array}{c}-4\\ 3\end{array}\right]=(A\left[\begin{array}{cc}\hat{i}& \hat{j}\end{array}\right])\vec{v} \end{gathered}$$

$det(A)=1\cdot 1-(-2)\cdot 0=1$
→ Area stays the same.
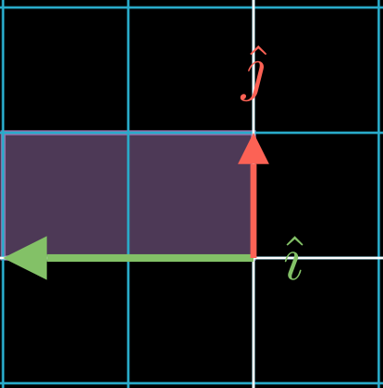
→ The unit vectors of the original vector space form the identity matrix.
→ The new unit vectors equal the columns of the transformation matrix:

If any of the diagonal entries are $0$, the matrix is not invertible/squashes the space to a lower dimension. If it is different from $0$, the matrix has full rank.

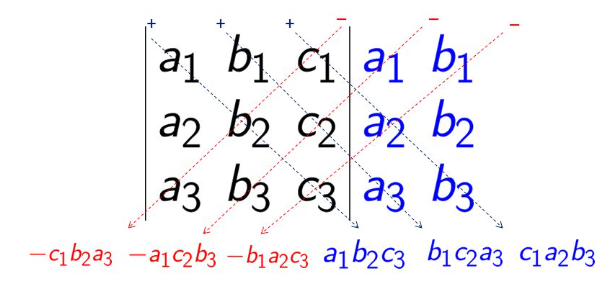
Rule of Sarrus for calculating determinantes for matrices up to $3\times 3$:

$$A=\left[\begin{array}{ccc}a& b& c\\ d& e& f\\ g& h& i\end{array}\right]$$ $$\det (A)=aei+bfg+cdh-ceg-bdi-afh$$

See cofactor expansion for a recursive method to compute determinants of larger matrices.

Determinant x linear systems of equations | Cramer’s Rule

A system of linear equations can be represented as a matrix equation $A\vec{x}=\vec{b}$.
If $A$ is invertible, we can solve for $\vec{x}$:

$$\vec{x}=A^{-1}\vec{b}$$

If $A$ is not invertible, there is either no solution or infinitely many solutions.
The determinant tells us whether $A$ is invertible (non-zero determinant) or not (zero determinant).

More concretely, consider the system of equations:

\begin{align} \text{I:}\quad & a_{11}x_{2} + a_{12}x_{2} = b_{1} \\ \text{II:}\quad & a_{21}x_{1} + a_{22}x_{2} = b_{2} \end{align} $$ We can solve for $x_{1}$ by multiplying I by $a_{22}$ and II by $-a_{12}$ and adding them: $$ \begin{align*} a_{22}(a_{11}x_{1} + a_{12}x_{2}) & = a_{22}b_{1} \\ -a_{12}(a_{21}x_{1} + a_{22}x_{2}) & = -a_{12}b_{2} \\ \hline (a_{11}a_{22} - a_{12}a_{21})x_{1} & = a_{22}b_{1} - a_{12}b_{2} \\ x_{1} & = \frac{a_{22}b_{1} - a_{12}b_{2}}{a_{11}a_{22} - a_{12}a_{21}} \end{align*} $$ Similarily, for $x_{2}$, we get: $$ x_{2} = \frac{a_{11}b_{2} - a_{21}b_{1}}{a_{11}a_{22} - a_{12}a_{21}} $$ Their common denominator for $x_{1}$ and $x_{2}$, $a_{11}a_{22} - a_{12}a_{21}$, is the determinant of the coefficient matrix! → If the determinant is zero, the equations are either parallel (no solution) or identical (infinitely many solutions). → There is redundancy in the equations, they do not span the entire 2D space. Furthermore, the numerators can be interpreted as determinants as well, so we can write the solutions as:

\begin{align*}
x_{1} &= \frac{\begin{vmatrix} b_{1} & a_{12} \ b_{2} & a_{22} \end{vmatrix}}{\begin{vmatrix} a_{11} & a_{12} \ a_{21} & a_{22} \end{vmatrix}} = \frac{1}{\det A} \begin{vmatrix} b_{1} & a_{12} \ b_{2} & a_{22} \end{vmatrix}, \quad \ \
x_{2} &= \frac{\begin{vmatrix} a_{11} & b_{1} \ a_{21} & b_{2} \end{vmatrix}}{\begin{vmatrix} a_{11} & a_{12} \ a_{21} & a_{22} \end{vmatrix}} = \frac{1}{\det A} \begin{vmatrix} a_{11} & b_{1} \ a_{21} & b_{2} \end{vmatrix}
\end{align*}

Or generally: > [!definition] Cramer's Rule > > Let $A \in \mathbb{R}^{n\times n}$ with $\det \ne 0$, and $b \in \mathbb{R}^{n}$. > Then, the linear system $A x = b$ has the *unique* solution $x = (x_{1}, \dots, x_{n})^{T}$ given by >$$ > x_{k} = \frac{\det(A_{k})}{\det(A)} >$$ > where $A_{k}$ is the matrix obtained by replacing the $k$-th column of $A$ with the vector $b$: >$$ > A_{k} = \begin{bmatrix} > | & & | & | & | & & | \\ > a_{1} & \dots & a_{k-1} & b & a_{k+1} & \cdots & a_{n} \\ > | & & | & | & | & & | > \end{bmatrix} >$$ > >> [!theorem]- Proof >>Define $X_k = (e_1, \ldots, e_{k-1}, x, e_{k+1}, \ldots, e_n)$ — the identity matrix with column $k$ replaced by the solution vector $x$. >> >>*Claim:* $\det(X_k) = x_k$ >> >>Row $k$ of $X_k$ is $(0, \ldots, 0, x_k, 0, \ldots, 0)$ since $e_j$ has a 1 only in row $j$, so columns $j \ne k$ contribute 0 to row $k$. >> Eliminate column $k$ using row $k$ (doesn't change det). >> Result: diagonal matrix with entries $(1, \ldots, 1, x_k, 1, \ldots, 1)$, so $\det(X_k) = x_k$. >> >>*Connection to $A_k$:* >>Column $j$ of $A \cdot X_k$ is $A e_j = a_j$ for $j \ne k$, and column $k$ is $Ax = b$. >>So $A \cdot X_k = A_k$, giving $\det(A_k) = \det(A) \cdot \det(X_k) = \det(A) \cdot x_k$, $\implies x_k = \frac{\det(A_k)}{\det(A)}$. >> >>> [!example]- Extra explicit >>>Why $\det(X_k) = x_k$ >>>$X_2 = \begin{pmatrix} 1 & x_1 & 0 \\ 0 & x_2 & 0 \\ 0 & x_3 & 1 \end{pmatrix}$ >>>we can just eliminate column 2 with row. >>>Why is $A \cdot X_{k} = A_{k}$? >>>E.g. $A \cdot X_2$: >>>$$ > A \cdot X_2 = A \cdot \begin{pmatrix} | & | & | \\ e_1 & x & e_3 \\ | & | & | \end{pmatrix} = \begin{pmatrix} | & | & | \\ Ae_1 & Ax & Ae_3 \\ | & | & | \end{pmatrix} >>> > $$ ___ In this concrete form we can also see the relation to the inverse matrix:

A^{-1} = \frac{1}{\det(A)} \begin{bmatrix} d && -b \ -c && a \end{bmatrix} = \frac{1}{ad-bc} \begin{bmatrix} d && -b \ -c && a \end{bmatrix}

## References [3b1b: The determinant | Chapter 6, Essence of linear algebra](https://youtu.be/Ip3X9LOh2dk) [18. Properties of Determinant (Gilbert)](https://youtu.be/srxexLishgY)