inverse matrix

Some square matrices have an inverse, which produce the identity matrix if you multiply them:

$$A^{-1}A=I$$

The inverse is commutative: $A^{-1}A=A{A}^{-1}$
Matrices that have an inverse are called invertible or non-singular.

A matrix is non-invertible / singular if:

• It is not a square matrix
• The determinant is 0
• $Ax=0$ | $x\ne 0$
• Its rows are not linearly independent (rows can be written as a linear combination of eachother? → dependent → singular)
  A matrix is invertible if:
• gaussian elimination produces a full set of pivots (a full-rank matrix)

The inverse of a diagonal matrix is easy:

$${\left[\begin{array}{cc}a& 0\\ 0& b\end{array}\right]}^{-1}=\left[\begin{array}{cc}\frac{1}{a}& 0\\ 0& \frac{1}{b}\end{array}\right]$$

Or generally: $D_{i,j}^{-1}=\frac{1}{D_{i,j}}$

Intuition + Examples

Negative case

Let’s have a look at a singular matrix:

$$A=\left[\begin{array}{cc}1& 3\\ 2& 6\end{array}\right]$$

Why is it not invertible?

a) Linear dependance

Its rows are a linear combination of eachother. They both lie on the same line going through the vector [1 2].

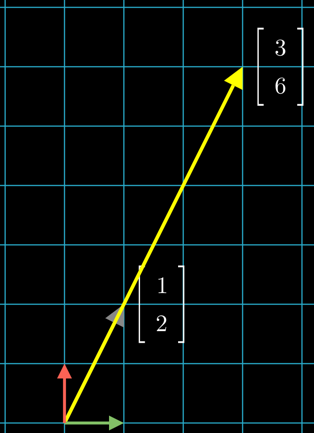
There is no combination of these vectors, which would yield the vectors of the identity matrix (red and green basis vectors).

There is redundancy in the information provided by the columns, and you can’t uniquely solve a system of linear equations that uses the matrix. This redundancy means that there is no unique inverse for this matrix.

b) $Ax=0$ | $x\ne 0$

We can find an $x$ that satisfies the above equation:

$$Ax=\left[\begin{array}{cc}1& 3\\ 2& 6\end{array}\right]\left[\begin{array}{c}3\\ -1\end{array}\right]=\left[\begin{array}{c}0\\ 0\end{array}\right]$$

Now suppose $A^{-1}$ exists, then $A^{-1}Ax=0$ only works if $x=0$.
→ If there is some $x$ for which $Ax=0$, there is no inverse matrix (such an $x$ exists due to the linear dependence of A’s vectors).

Positive case (finding the determinant)

Gauss-Jordan

$$\underset{A}{\underbrace{\left[\begin{array}{cc}1& 3\\ 2& 7\end{array}\right]}}\underset{A^{-1}}{\underbrace{\left[\begin{array}{cc}a& c\\ b& d\end{array}\right]}}=\underset{I}{\underbrace{\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]}}$$

A is invertible, since $det(A)$ is positive / the vectors are pointing in different directions.

Now finding the Inverse is just like solving two systems of linear equations!

$$\begin{gathered} \left[\begin{array}{cc}1& 3\\ 2& 7\end{array}\right]\left[\begin{array}{c}a\\ b\end{array}\right]=\left[\begin{array}{c}1\\ 0\end{array}\right] \\ \left[\begin{array}{cc}1& 3\\ 2& 7\end{array}\right]\left[\begin{array}{c}c\\ d\end{array}\right]=\left[\begin{array}{c}0\\ 1\end{array}\right] \end{gathered}$$

By the gauss-jordan method, we can solve them at once, by augmenting the matrix, i.e. carrying the right side of the equations with us / applying the same elimination steps to it. Our goal is to transform $A$ into $I$. By the end of the elimination, the augmented part will have turned into the inverse matrix:

$$\begin{gathered} \left[\begin{array}{cccc}1& 3& 1& 0\\ 2& 7& 0& 1\end{array}\right]\stackrel{E_{2,1}}{\to }\left[\begin{array}{cccc}1& 3& 1& 0\\ 0& 1& -2& 1\end{array}\right]\stackrel{E_{1,2}}{\to }\left[\begin{array}{cccc}1& 0& 7& -1\\ 0& 1& -2& 1\end{array}\right] \\ {A}^{-1}=\left[\begin{array}{cc}7& -1\\ -2& 1\end{array}\right] \end{gathered}$$

So we applied an elimination $E=E_{2,1}{E}_{1,2}$ to $[AI]$, such that $A$ turns into the inverse, so by definition, $E$ is the inverse:

$$E\left[AI\right]=\left[I{A}^{-1}\right]$$

We discovered it step by step, as we multiplied the partial $E$‘s with the identity.
$EA=I\to E=A^{-1}$

My first intuition was to view it like this:
It’s just like the usual transformations when solving equations
($\underset{(I)}{\frac{A}{A}}(A^{-1})=\underset{(A^{-1})}{\frac{I}{A}}$, just imagine matrices being divisible).

Solving the systems of equations traditionally / explicitly

Another (crude) way of solving it.
This is how we did it in class (first):

$$\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right]\left[\begin{array}{ccc}a& b& c\\ d& e& f\\ g& h& i\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$

The matrix multiplication consists of 3 separate systems of equations:

$$\begin{array}{rl}1a+2d+3g& =1\\ 4a+5d+6g& =0\\ 7a+8d+9g& =0\\ a=\dots ,d=\dots & ,g=\dots \\ 1b+2e+3h& =0\\ 4b+5e+6h& =1\\ 7b+8e+9h& =0\\ b=\dots ,e=\dots & ,h=\dots \\ 1c+2f+3i& =0\\ 4c+5f+6i& =0\\ 7c+8f+9i& =1\\ c=\dots ,g=\dots & ,i=\dots \end{array}$$

Adjugate determinant method

Another “interesting” method we learned in school:

One can write down the inverse of an invertible matrix by computing its cofactors by using Cramer’s rule, as follows. The matrix formed by all of the cofactors of a square matrix A is called the cofactor matrix (also called the matrix of cofactors or, sometimes, comatrix):
Then the inverse of A is the transpose of the cofactor matrix times the reciprocal of the determinant of A: ¹

$$\begin{array}{rl}{A}^{-1}& =\frac{1}{\det (A)}{C}^T\\ & \\ \text{e.g.:}& \\ A& =\left[\begin{array}{cc}{a}_{1,1}& a_{1,2}\\ a_{2,1}& a_{2,2}\end{array}\right]\\ A^{-1}& =\frac{1}{\det (A)}\cdot \left[\begin{array}{cc}{a}_{2,2}& -a_{1,2}\\ -a_{2,1}& a_{1,1}\end{array}\right]\end{array}$$

The transpose of the cofactor matrix $C^T$ is called the adjucate.

References

Gilbert Strang Lecture 3: Multiplication and inverse matrices
Quote of the lecture (that some math teachers should rlly take to heart): “It’s good to keep the computations manageable and let the ideas come out”

matrix

Footnotes

1. https://en.wikipedia.org/wiki/Minor_(linear_algebra)#Inverse_of_a_matrix ↩