generalization error

The generalization error or risk is the exptected loss on future data for a given model $f(\cdot ;\theta )$ with parameters $\theta$, defined as:

$$\begin{array}{rl}R(f(\cdot ;\theta ))& =\mathbb{E}[\mathcal{L}(f(x;\theta ),y)]\\ & ={\int }_{\mathcal{X}}{\int }_{\mathcal{Y}}\mathcal{L}(f(x;\theta ),y)p(x,y)dydx\end{array}$$

where $\mathcal{L}(\hat{y},y)$ is the loss function, and $p(x,y)$ is the true (unknown) joint distribution of inputs $x$ and outputs $y$.

We estimate the generalization error using the empirical risk (or training error) computed on a finite training dataset $\{(x_i,y_i){\}}_{i=1}^n$:

$$\hat{R}(f(\cdot ;\theta ))=\frac{1}{n}\sum _{i=1}^n\mathcal{L}(f(x_i;\theta ),y_i)$$

This works under the assumption that the training data is drawn iid from the same distribution as future data, and by the law of large numbers, the empirical risk converges to the true risk as $n\to \infty$.

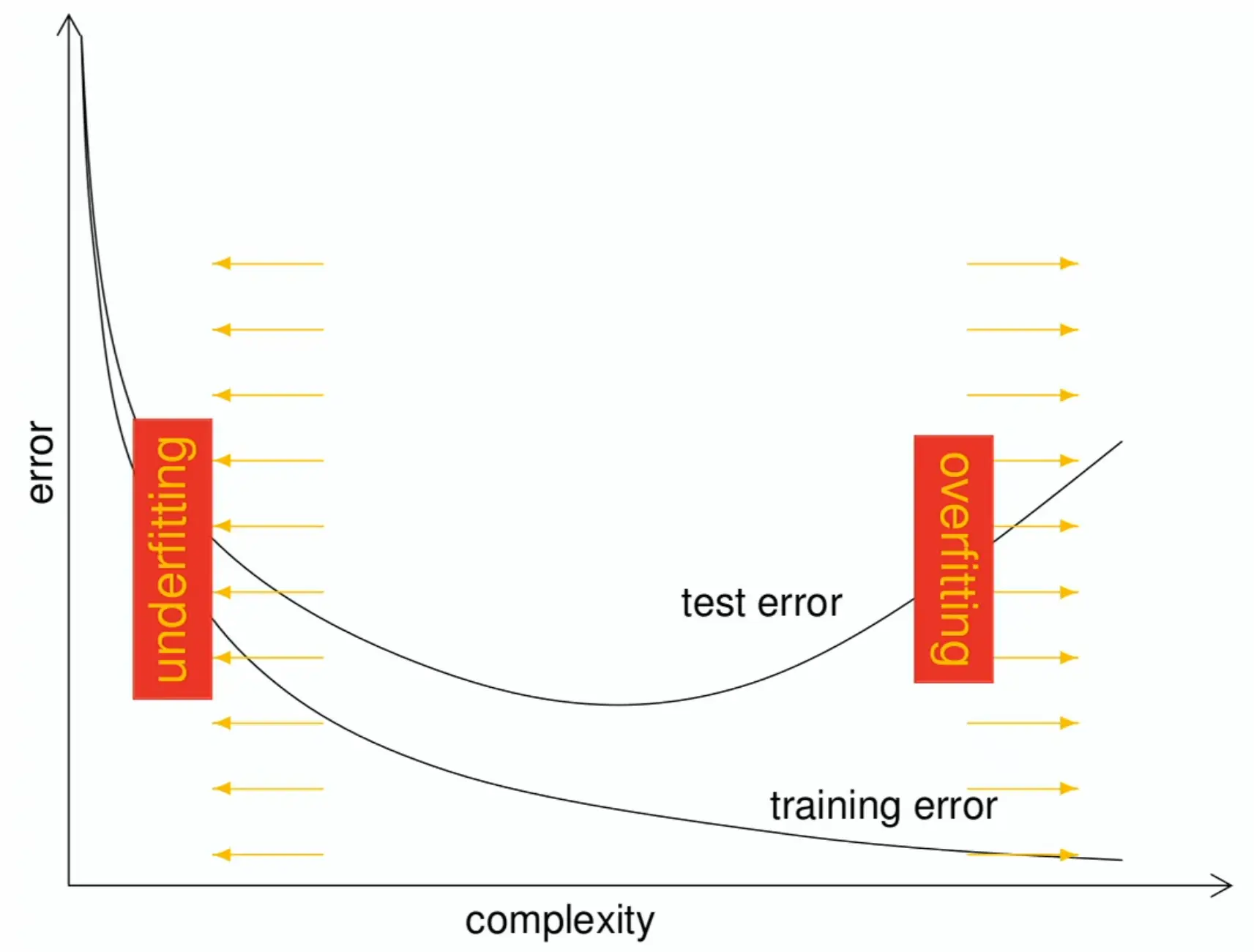
The bias-variance tradeoff in supervised learning

If we train plain empirical risk minimization (ERM), we run the risk of overfitting, where the model fits the training data well (low empirical risk) but performs poorly on unseen data (high generalization error), aka high variance.

→ Assume data samples are iid and partition data into training and validation/test sets to estimate generalization error, e.g. using cross-validation. Validation sets for hyperparameter tuning, to avoid data overlaps/leakage.
→ Use regularization techniques (like L2 regularization, dropout, data augmentation) to reduce overfitting and improve generalization.

The sweetspot is where train and test errors align.

Link to original