batch gradient descent

Batch gradient descent

Batch gradient descent computes the gradient of the loss function using the entire dataset at each iteration before updating the parameters:

$${\theta }_{t+1}={\theta }_t-\alpha {\nabla }_{\theta }J({\theta }_t)={\theta }_t-\alpha \frac{1}{n}\sum _{i=1}^n{\nabla }_{\theta }L(x_i,y_i,{\theta }_t)$$

where $n$ is the total number of training examples, $\alpha$ is the learning rate, and $L$ is the loss function for individual examples.

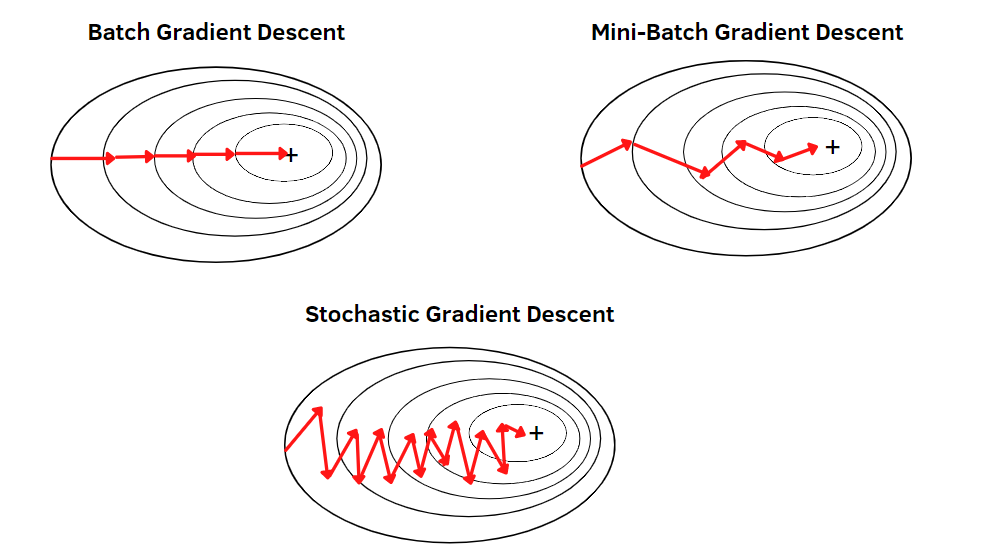
Exact gradient computation

Since batch gradient descent uses all training data, it computes the exact gradient of the empircal risk. This leads to smooth, deterministic updates that always move in the direction of steepest descent for the entire dataset.

Trade-offs of batch gradient descent

Advantages:
Guaranteed convergence to local minimum (for convex functions) or critical point.
Stable and predictable optimization trajectory.
Can leverage vectorized operations efficiently.

Disadvantages:
Computationally expensive for large datasets - requires full dataset pass for single update.
Memory intensive - entire dataset must fit in memory.
No inherent regularization from gradient noise.

Each iteration processes the complete dataset (batch size = $n$), making it distinct from mini-batch gradient descent (batch size between 1 and $n$) and SGD (batch size = 1).

References

gradient descent
optimization
mini-batch gradient descent