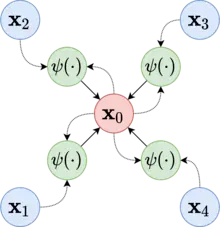
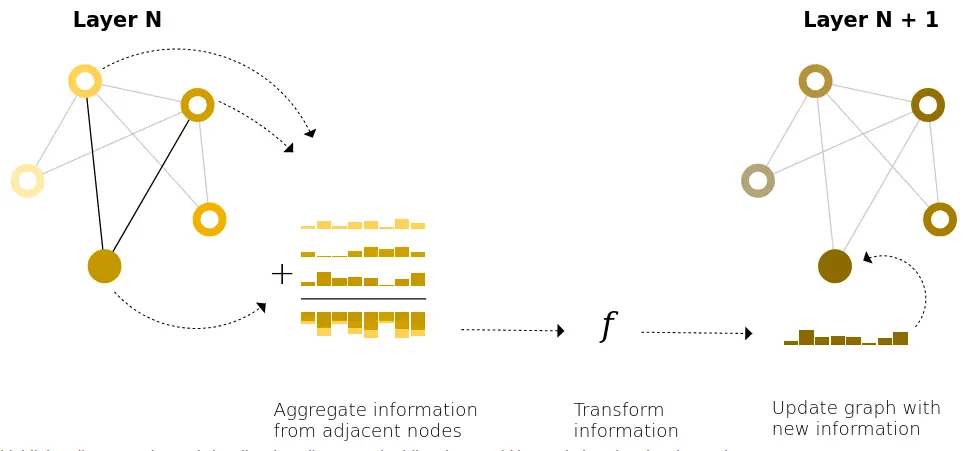
message passing

Message passing is a generalization of the convolution operation to graphs: We aggregate information from neighbouring nodes, but neighbours can vary in number and arrangement.

EXAMPLE

transformers are GNNs, communicating via message passing on (usually) complete graphs of tokens.
graph convolutional network

Message passing layer

$${\mathbf{h}}_u=\varphi \left(x_u,\underset{v\in N_u}{⨁}\psi ({\mathbf{x}}_u,{\mathbf{x}}_v,{\mathbf{e}}_{uv})\right)$$

$G=(V,E)$ … some graph.
$N_u$ … neighbourhood of some node $u\in V$.
${\mathbf{x}}_u$ … features of $u$.
${\mathbf{e}}_{uv}$ features of edge $(u,v)\in E$ (other features can also be used).
$\varphi :{\mathbb{R}}^k\times {\mathbb{R}}^k\to {\mathbb{R}}^l$ … message function (differentiable / neural network).
$\psi :{\mathbb{R}}^k\times {\mathbb{R}}^k\to {\mathbb{R}}^l$ … readout function (differentiable / neural network).
$⨁$ … permutation invariant aggregation operator (like $\sum$, or $\max$, or $\text{attention}$).
${\mathbf{h}}_u$ … output representation for node $u$.

The equation describes pairwise communication between nodes.

Node ${\mathbf{x}}_0$ receives messages sent by all of its immediate neighbours ${\mathbf{x}}_1$ to ${\mathbf{x}}_4$. Messages are computing via the message function $\varphi$, which accounts for the features of both senders and receiver.

A simple type of “message passing” in GNNs is simply aggregating information from adjacent nodes to compute the next embedding for a node (in conjunction with the nodes own embedding).

For a GNN with $k$ layers, each node can aggregate information from nodes $k$ steps away.
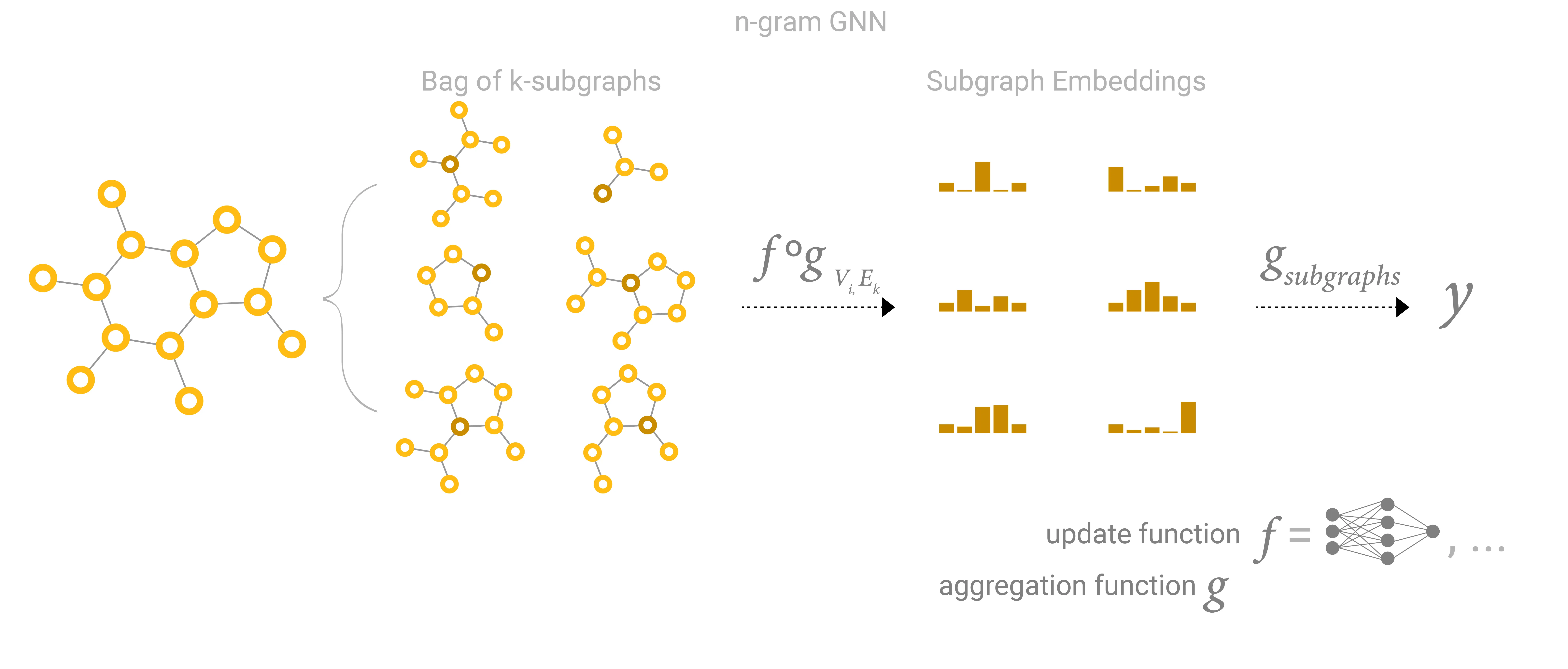
This can also be viewed as collecting all possible subgraphs of size $k$ and learning vector representations from the vantage point of one node or edge:

For large graphs, it may become infeasible (or even detrimental - see below) to add enough layers for every node to communicate with eachother, however, you can add a global context vector / master node / global representation which acts like a bridge for communication between nodes.

While GNNs generally scale with the number of layers, having many layers can even be detrimental, as representations get “diluted” from broadcasting many successive iterations.

GNNs are surprisingly parameter efficient.

Aggregation functions

There is no operation that is uniformly the best choice. The mean operation can be useful when nodes have a highly-variable number of neighbors or you need a normalized view of the features of a local neighborhood. The max operation can be useful when you want to highlight single salient features in local neighborhoods. Sum provides a balance between these two, by providing a snapshot of the local distribution of features, but because it is not normalized, can also highlight outliers. In practice, sum is commonly used.

If you measure the similarity of every node $q$ and its neighbours $\mathbf{k}$, via dot-products and then take the softmax and a weighted sum of the node features, you’ve almost got self-attention. Just that in self-attention, we make separate projections for Q,K, and V, in order to increase the expressivity of the scoring mechanism.

Parallels to convolutions

Aggregation = downsampling / pooling.
Number of graph layers = kernel size.

For larger graphs, not every node can receive info from every node, even though it might need to in order to classify correctly.

Full-graph message passing is expensive (quadratic in number of nodes), but strictly more powerful (general; and performant in practice, as the success of self-attention has shown).

But the research into sparse attention is active and ongoing (most promising: NSA).

Other mitigation strategies include: adding a global context vector / master node / global representation which acts like a bridge for communication between nodes; or using hierarchical pooling to create a coarser graph.

MPGNN with registers?

→ NCA?

1-WL Expressiveness Is (Almost) All You Need

References

MESSAGE PASSING ALL THE WAY UP

https://en.wikipedia.org/wiki/Graph_neural_network
distill gnn intro