… matrix with rows and columns, where element is located at the intersection of row and column .
Here, is a 3x3 matrix.
The main diagonal goes from top left to bottom right.
A matrix can be viewed as a mapping from one vector space to another
The equation is solvable iff is contained in the range of .
There is a unique solution iff is invertible ( bijective). This is only possible if is a square matrix with full rank, i.e. all rows and cols are linearly independent.
The set of matrices of same dimensions is not a field because matrix multiplication is not commutative and not every matrix every matrix has an inverse.
It is however a ring with 1.
Common notation
┌ ── a₁ᵀ ── ┐ A = │ ── a₂ᵀ ── │ = ( c₁ c₂ c₃ ) │ ── a₃ᵀ ── │ └ ┘ row view column view ```
Matrix operations
Addition and subtraction
Let and be two 2x2 matrices:
Their elementwise addition / subtraction, denoted by , is given by:
Scalar multiplication
Let be a 2x2 matrix and be a scalar:
Scalar multiplication, denoted by , is given by:
Matrix multiplication
Let and be two 2x2 matrices:
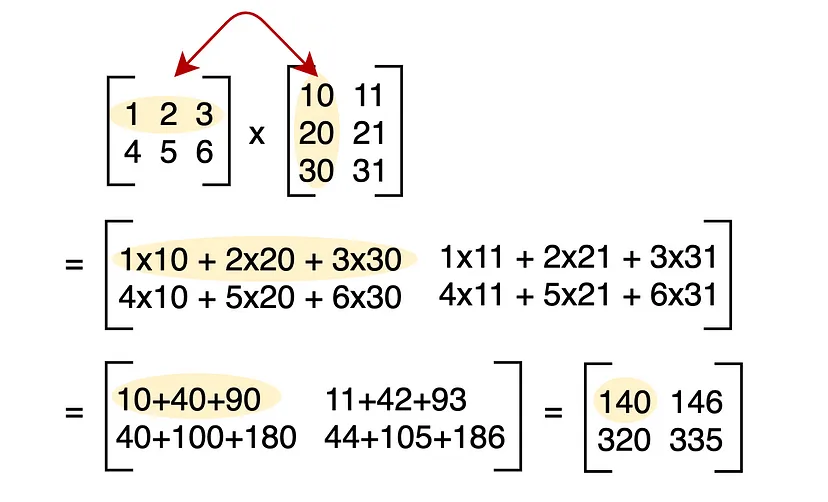
Matrix multiplication, denoted by , is given by:
The entry comes from row of and column of (the dot product ).
E.g.:
Visually: Matrix Multiplication.html
Intuitions
Viewing it from a col / row perspectve
Multiplying a matrix with a vector, results in a new vector, which is a linear combination of the columns of that matrix:
We have
Multiplying a row with a matrix gives us a new row, which is a linear combinations of the rows of that matrix:
We have
Let’s multiply a row by a column:
We can see that the resulting rows are multiples of the rows of and the resulitng colums are multiples of the columns of .
If plotted, all the rows of would be on the same line, the one of the vector [1 6].
The row-space (all possible linear combinations of rows of that matrix) is a line. The same goes for the column-space. 1
Viewing it as: AB = sum of ((cols of A) x (rows of B))
Block matmul
We can also for example cut two 16x16 matrices both into 4x 4x4 matrices, multiply those individually and will still get the same result (example).
Which permutation matrix flips the rows of a matrix, such that ?
Well, we first want 0 of the first row, 1 of the second row. And then 1 of the first row and zero of the second row, so: . It is the opposite of the Identity matrix.
Which matrix flips the columns of the matrix, such that ?
Answer: None. If we multiply on the left of the matrix, we are always doing row operations. To switch the columns, then: .
To do col ops, the matrix multiplies on the right, to do row ops, the matrix multiplies on the left.
Rules
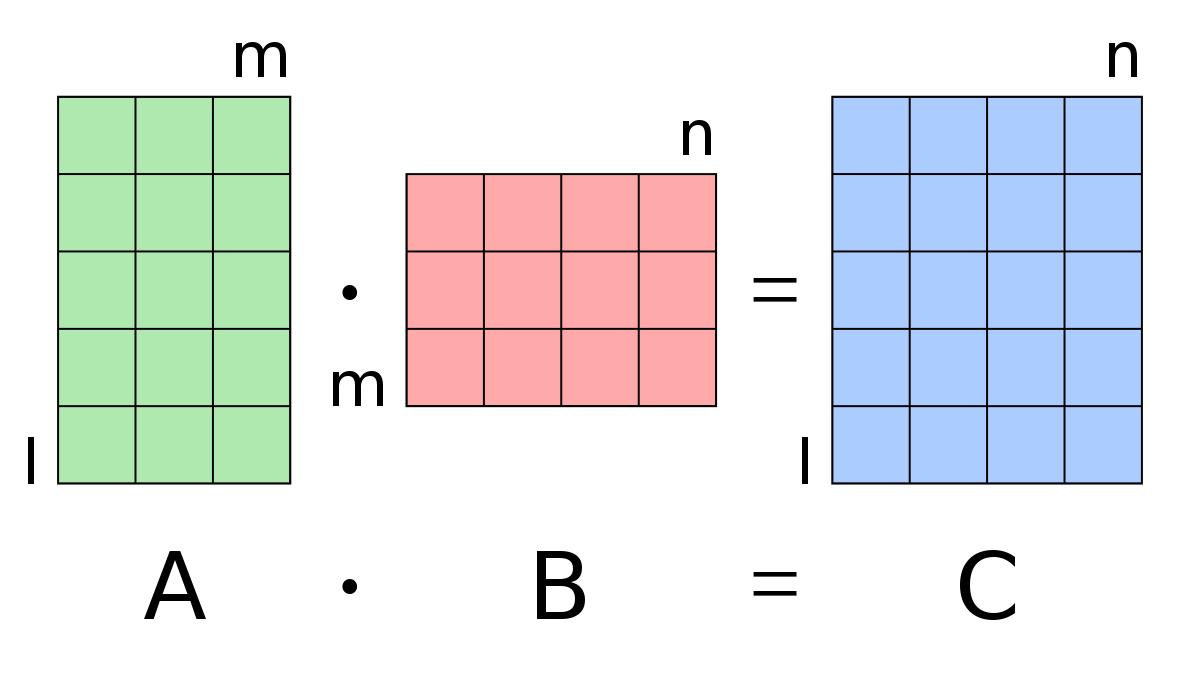
- Dimensions: Ensure has dimensions and has dimensions . The resulting matrix will have dimensions .
- Order matters: In general, . (Not commutative)
- Associative property: for any matrices , , and with compatible dimensions.
- Distributive property: and for matrices with compatible dimensions.
Division
Division is not defined because matrix multiplication is not commutative and there is not always an inverse to a matrix.
So if the division two matrices and is defined as:
If is not defined, we have a problem.
Transpose
Given a matrix , its transpose is obtained by flipping the matrix over its diagonal. This swaps the row and column indices of each element. If
The transpose operation has the following properties:
- The transpose of a transpose is the original matrix: .
- The transpose of a sum is the sum of the transposes: .
- The transpose of a product is the product of the transposes in reverse order: .
- The transpose of a scalar multiple is the scalar multiple of the transpose: .
Note: The diagonal of a matrix remains the same in the transpose.
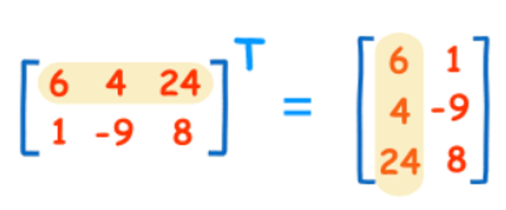
determinant
Types of matrices
Row matrix
A matrix with only one row and any number of columns.
Column matrix
A matrix with only one column and any number of rows. Aka vector, aka column.
Zero matrix
A matrix in which all the elements are zero.
Square matrix
A matrix with an equal number of rows and columns.
diagonal matrix
A matrix with nonzero elements only on the main diagonal.
Identity matrix
A square matrix with 1s on the main diagonal and 0s elsewhere. Any matrix multiplied by its identity matrix results in the same matrix: $$
A = I_mA = AI_n
$$$\forall \space A \in \mathbb{R}^{m \times n}I_mI_nAI \equiv E$ (for “Einheitsmatrix”).
Triangular matrix
An upper/lower triangular matrix is a square matrix, where all the elements below/above the main diagonal are zero, e.g.:
References
Visual Kernel YT Channel with visualizations of different matrices, spectral decomposition, SVD, …
Matrix Calculus (for Machine Learning and Beyond)
Footnotes
-
See Linear dependance for an example. ↩