isomorph

Isomorphism

Let $(G,\circ ),(H,\star )$ be groups. A function $\varphi :G\to H$ is an isomorphism if:

1. $\varphi$ is a homomorphism
2. $\varphi$ is bijective

If any such an isomorphism exists, we say $G$ and $H$ are isomorphic, written $G\cong H$.

Isomorphic means "equal shape". Isomorphic groups are structurally identical, even if their elements and operations appear different. Things that apply to one group also apply to the other.

Difference to Homomorphisms

A homomorphism only requires structure preservation ($\varphi (x\circ y)=\varphi (x)\star \varphi (y)$), allows for many-to-one mappings.
An isomorphism additionally requires that $\varphi$ is bijective, meaning it is a one-to-one mapping.

• Every element in $H$ is reached (surjectivity)
• Different elements in $G$ map to different elements in $H$ (injectivity)

An isomorphism is a homomorphism that has an inverse homomorphism. Thus, isomorphic groups are structurally indistinguishable – they are essentially "the same group" written in different notation.

Properties of Isomorphic Groups

If $G\cong H$, then:
$G$ and $H$ have the same order (cardinality).
Every structural property is shared: commutativity, cyclic nature, order of elements, …
The groups are identical up to renaming of elements.

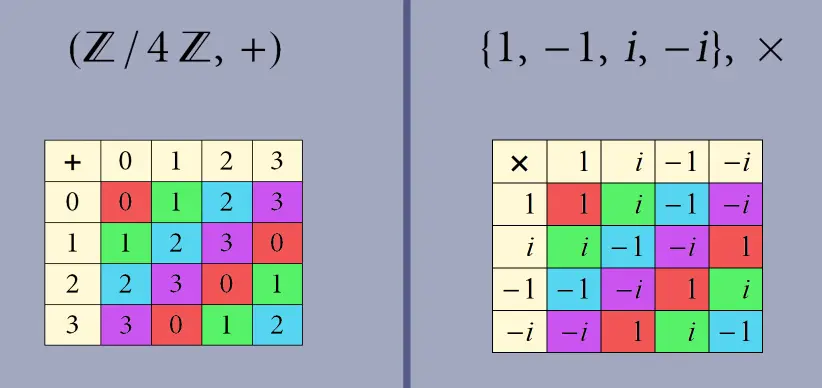
$({\mathbb{Z}}_4,+,\bar{1})\cong (\{1,i,-1,-i\},\cdot ,i)$ as both are cyclic groups of order 4, although their elements and operations appear different.

For an isomorphism $\varphi :G\to H$:

$\ker (\varphi )=\{e_G\}$ (equivalent to injectivity)
$\text{im}(\varphi )=H$ (equivalent to surjectivity)
${\varphi }^{-1}:H\to G$ exists and is also an isomorphism