cyclic group

Cyclic subgroup: For any element $g$ in a group $G$, one can form the subgroup $⟨g⟩=\{g^k\in \mathbb{Z}\}$, which is called the cyclic subgroup generated by $g$.

The order of $G$ is $|⟨g⟩|$, the number of elements in $⟨g⟩$.

If the order of element $a$ of $G$ is infinite, then the subgroup generated by $a$ is infinite as well, no cycle:
${\text{ord}}_G(a)=\infty ⟹|⟨a⟩|=\infty$

If the order of element $a$ of $G$ is finite, then the subgroup generated by $a$ is finite as well, forming a cycle:
${\text{ord}}_G(a)=k<\infty ⟹⟨a⟩=\{e,a,a^2,\dots ,a^{k-1}\},a^{n+{\text{ord}}_G(a)}=a^n$

As a congruence: $a^n\equiv a^m\mathrm{mod}{\text{ord}}_G(a)⟺n\equiv m\mathrm{mod}{\text{ord}}_G(a)$

$a^{|G|}=e$, for all $a\in G,g<\infty$

From lagrange’s theorem: $|⟨a⟩|=k={\text{ord}}_G(a)⟹{\text{ord}}_G(a)\mid |G|$, for $|G|<\infty$
In words: the order of an element in a finite group divides the order of the group, and the element raised to the power of the group order is the neutral element (one full cycle).

A cyclic group is a group which is equal to one of its cyclic subgroups: $G=⟨g⟩$ for some element $g$, called a generator.

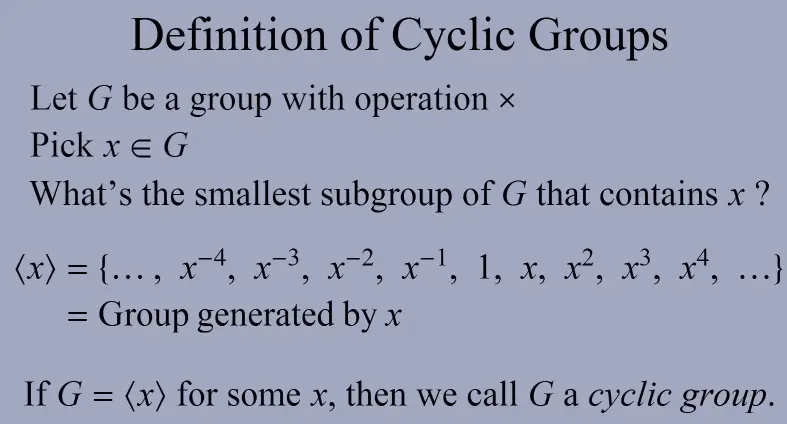
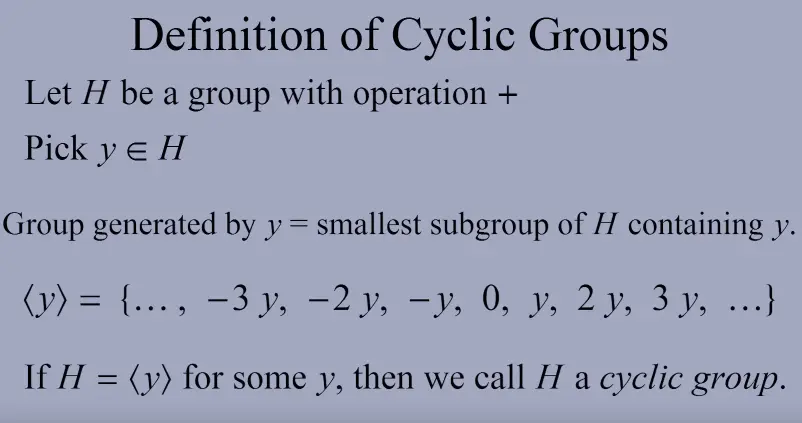
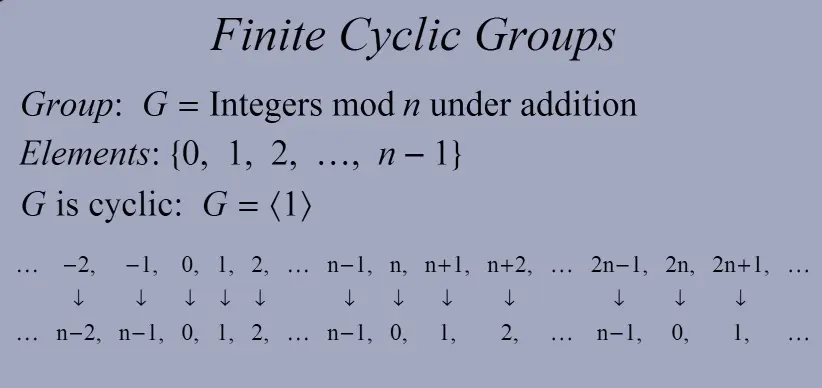
The set of all powers of $a$: $⟨a⟩:=\{a^n\mid n\in \mathbb{Z}\}$

Let $(G,\circ )$ be a group and $\exists a\in G:⟨a⟩=G$, then $⟨a⟩$, is a cyclic subgroup of $G$, generated by $a$ (“von $a$ erzeugte Untergruppe”).

$a\le G$, … is it actually a subgroup?
Note empty: $a^0=e\in ⟨a⟩⟹⟨a⟩\ne \varnothing$
Closed: $x,y\in ⟨a⟩⟹\exists n,m\in \mathbb{Z}:x=a^n,y=a^m⟹x\circ y=a^n{a}^m=a^{n+m}\in ⟨a⟩$ → $⟨a⟩$ abelian group
Invertible: $x\in ⟨a⟩⟹\exists n\in \mathbb{Z}:x=a^n⟹x^{-1}=a^{-n}⟹a^{-n}\in ⟨a⟩$ (because $a^n{a}^{-n}=a^0=e)$
$✓$

The integers mod n are a cyclic group:

Example quotient group

Consider the integers under addition $G=(\mathbb{Z},+)$ and the normal subgroup $N=n\mathbb{Z}$ of multiples of $n$.
The quotient group $(\mathbb{Z}/n\mathbb{Z},+)$ aka $({\mathbb{Z}}_n,+)$ consists of the following cosets:

$$\begin{array}{rl}\mathbb{Z}/n\mathbb{Z}& =\{0+n\mathbb{Z},1+n\mathbb{Z},\dots ,(n-1)+n\mathbb{Z}\}\\ & =\{\bar{0},\bar{1},\dots ,\overline{n-1}\}\\ & ={\mathbb{Z}}_n\end{array}$$

Note: This quotient group is isomorphic to the cyclic group of order $n$, generated by the congruence class $\bar{1}$: $C_n=⟨\bar{1}⟩$

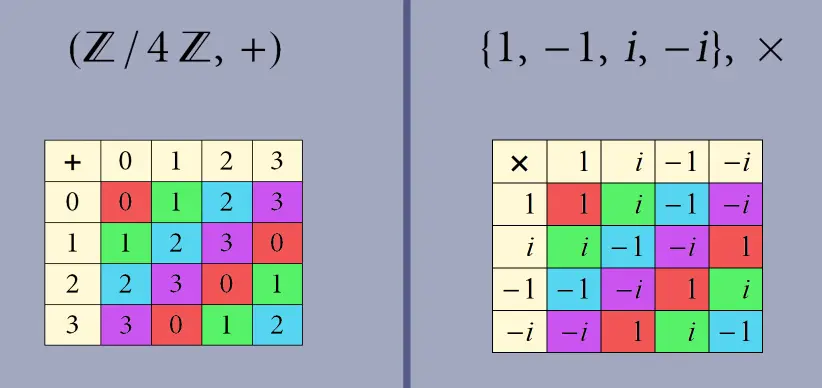
For instance, in $(\mathbb{Z}/3\mathbb{Z},+)$ : $(1+3\mathbb{Z})+(2+3\mathbb{Z})=3+3\mathbb{Z}=0+3\mathbb{Z}$ $⟺$ arithmetic in ${\mathbb{Z}}_3$.

Link to original

$({\mathbb{Z}}_4,+,\bar{1})\cong (\{1,i,-1,-i\},\cdot ,i)$ as both are cyclic groups of order 4, although their elements and operations appear different.

Link to original

Group homomorphism between congruence classes and roots of unity

Consider the groups $G=(\mathbb{Z},+)$ and $H=\{{\zeta }_m,{\zeta }_m^2,\dots ,{\zeta }_m^{m-1},{\zeta }_m^m=1\}$ where ${\zeta }_m=\sqrt[m]{1}=e^{2\pi i/m}$ is a primitive $m^{\text{th}}$ root of unity (i.e. the first one that’s not just $1$).

Define the map:

$$\begin{array}{rl}\varphi :\mathbb{Z}& \to H\\ n& \mapsto {\zeta }_m^n=e^{2\pi i(n/m)}\end{array}$$

To verify this is a homomorphism, we check if it preserves the group operation (addition in $\mathbb{Z}$ maps to multiplication in $H$):

$$\varphi (l+n)={\zeta }_m^{l+n}={\zeta }_m^l\cdot {\zeta }_m^n=\varphi (l)\varphi (n)$$

This is a surjective homomorphism since it covers all of $H$.
To find the kernel, we solve for all $x$ where:

$$\begin{array}{rl}\ker (\varphi )& =\{x\in \mathbb{Z}\mid \varphi (x)=1\}\\ & =\{x\in \mathbb{Z}\mid {\zeta }_m^x=1\}\\ & =\{x\in \mathbb{Z}\mid e^{2\pi i(x/m)}=1\}\\ & =m\mathbb{Z}\end{array}$$

The last step follows because $e^{2\pi i(x/m)}=1$ exactly when $x/m$ is an integer.

Applying the First Isomorphism Theorem:

$$\mathbb{Z}/m\mathbb{Z}={\mathbb{Z}}_m\cong H$$

Both ${\mathbb{Z}}_m$ and $H$ are cyclic groups of order $m$: In ${\mathbb{Z}}_m$ we add 1 repeatedly modulo $m$, while in $H$ we multiply by ${\zeta }_m$ repeatedly until returning to 1 after $m$ steps.

Link to original