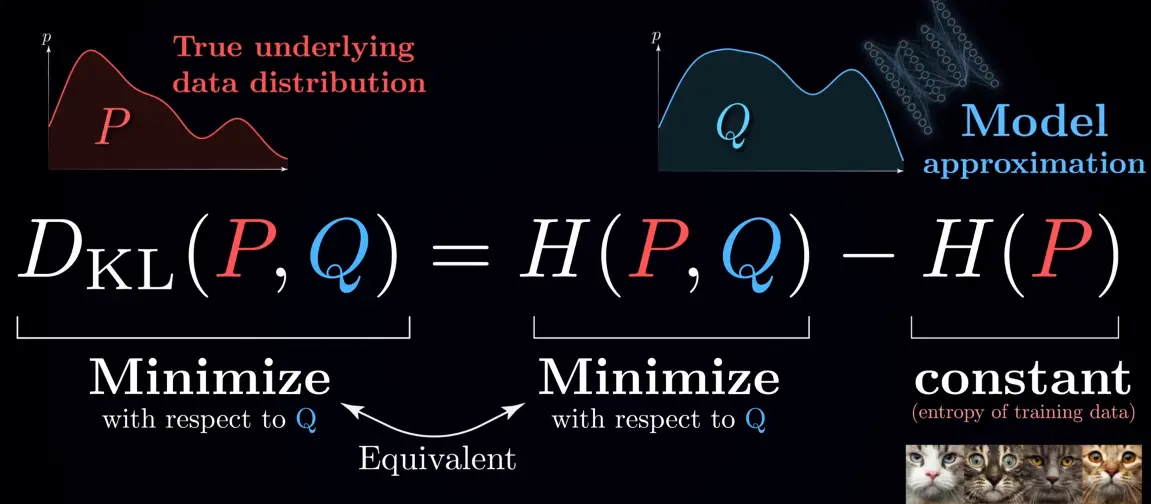
KL-divergence

KL-Divergence

The KL divergence measures the difference between the probability distribution of a model $Q$ and the true distribution $P$, i.e. the cross-entropy, disregarding the entropy of the true distribution itself:

$$\begin{array}{rl}{D}_{KL}(P||Q)& =H(P,Q)-H(P)\\ & ={\mathbb{E}}_{x\sim P}[-\log q(x)]-{\mathbb{E}}_{x\sim P}[-\log p(x)]\\ & ={\mathbb{E}}_{x\sim P}[\log \frac{p(x)}{q(x)}]\end{array}$$

It’s extra average surprise, aka information-theoretic regret, when assuming model $Q$ instead of the true distribution $P$.
In base 2, we get the inefficiency of using $Q$ to encode $P$ in bits

The $\Vert$ notation emphasizes that the KL divergence is not symmetric: ¹

$P$ and $Q$ are not interchangable

$$H(P,Q)\ne H(Q,P)$$

E.g.: If you believe a coin is fair (0.5/0.5), but it is rigged (0.99/0.01), then the CE is: $0.99\log \left(\frac{1}{0.5}\right)+0.01\log (\frac{1}{0.5})\approx 0.7$
If you believe it is rigged when it is actually fair, then the CE is: $0.5\log \left(\frac{1}{0.99}\right)+0.5\log (\frac{1}{0.01})\approx 2.4$
In the second case, the entropy is much larger, as half of the time you are extremely surprsied to see tails, this extreme surprise dominates the average surprise.

Link to original

KL divergence is not a metric (distance) because it is not symmetric! $D_{KL}(P||Q)\ne D_{KL}(Q||P)$

→ When using KL divergence as a loss function, the choice of which distribution is the “reference” (P) versus the “approximation” (Q) matters significantly. For example, minimizing $D_{KL}(P||Q)$ tends to produce Q that covers all modes of P (zero-avoiding), while minimizing $D_{KL}(Q||P)$ produces Q that concentrates on high-probability regions of P (zero-forcing).

Here’s a visualization of the difference / KL in general: https://claude.ai/public/artifacts/56ba13ac-42cc-4328-9fa2-32294ebe0345

Reverse KL

We’re using the reverse $D_{KL}(q||p)$ , with $p$ and $q$ swapped, because the forward KL would require us to sample from the posterior which we can’t compute and need variational inference for in the first place.
Note: $q$ is always the thing we’re optimizing when using KL

Behavioral differences:
$D_{KL}(p||q)$ (forward KL) is “mass-covering”: weighted by $p$, it tries to cover everything, penalizing $q$ for not putting mass where $p$ has mass

$D_{\text{KL}}(q||p)$ (reverse KL) is “mode-seeking”: weighted by $q$, it focuses on the main modes of $p$, penalizing $q$ for putting mass where $p$ is low
→ tends to underfit rather than overfit

Link to original

Why aren’t we using KL-divergence as a loss function, if it seems to have better properties?

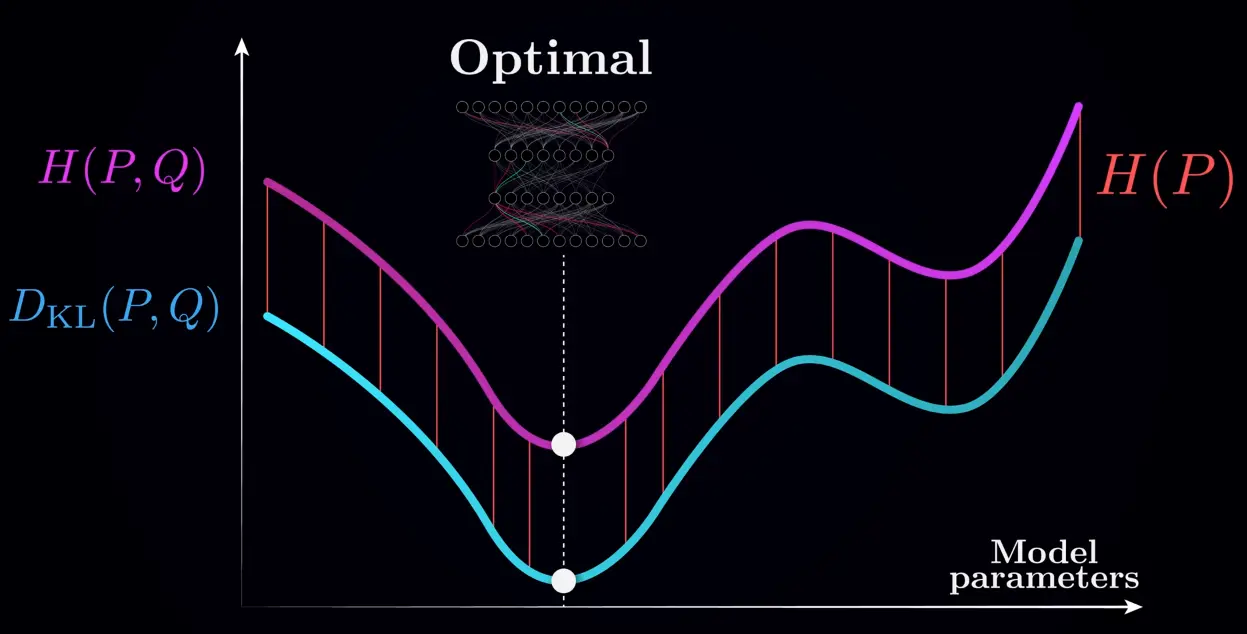
Since we cannot change $P$, we can only minimize w.r.t. $Q$, and hence the KL divergence is equivalent to cross-entropy loss:

We don’t care about the exact value, so we don’t bother to estimate the entropy of the training data:

References

The Key Equation Behind Probability

Footnotes

1. Don’t ask me why cross-entropy doesn’t have the same notation. Maybe because it’s because KL-divergence could otherwise be more easily confused with a distance? ↩