The Sensory Neuron as a Transformer Permutation-Invariant Neural Networks for Reinforcement Learning

year: 2021
paper: https://arxiv.org/pdf/2109.02869.pdf
website: https://attentionneuron.github.io/ | https://blog.otoro.net/2021/11/18/attentionneuron/
code: https://paperswithcode.com/paper/the-sensory-neuron-as-a-transformer
connections: transformer, reinforcement learning, permutation invariance, meta learning, self-organization, cma-es, permutation invariance, david ha

---

Author YT (13min)
Paper walkthrough YT (33min; Aleksa Gordic)
1h Equations and code walkthrough

Motivation

Humans can adapt to new input fashions:
Riding bike with left/right steering reversed, blind people see if they receive the information through a different medium. This paper aims to do that without re-training (and immediatly, brain takes days - weeks - months). Data is not just simply shuffled during training to memorize.
Helpful in Robotics (crosswiring, complex input output mappings) + Fault tolerance: filters out noisy channels to identify ones with relevant info. + …

Abstract

In complex systems, we often observe complex global behavior emerge from a collection of agents interacting with each other in their environment, with each individual agent acting only on locally available information, without knowing the full picture. Such systems have inspired development of artificial intelligence algorithms in areas such as swarm optimization and cellular automata. Motivated by the emergence of collective behavior from complex cellular systems, we build systems that feed each sensory input from the environment into distinct, but identical neural networks, each with no fixed relationship with one another. We show that these sensory networks can be trained to integrate information received locally, and through communication via an attention mechanism, can collectively produce a globally coherent policy. Moreover, the system can still perform its task even if the ordering of its inputs is randomly permuted several times during an episode. These permutation invariant systems also display useful robustness and generalization properties that are broadly applicable. Interactive demo and videos of our results: https://attentionneuron.github.io/

Temporal observations: For RNNs, the LSTM maintains internal state across timesteps. For FNNs, they stack 4 consecutive frames as input (e.g., for vision: $o_t\in R^{H\times W\times 4}$).

Why actions as additional input?

Since the ordering of the input is arbitrary, each sensory neuron is required to interpret and identify their received signal. To achieve this, we want $f_k(o_t[i],a_{t-1})$ to have temporal memories. In practice, we find both RNNs and feed-forward neural networks (FNN) with stacked observations work well, with FNNs being more practical for environments with high dimensional observations.
In addition to the temporal memory, including previous actions is important for the input identification too. Although the former allows the neurons to infer the input signals based on the characteristics of the temporal stream, this may not be sufficient. For example, when controlling a legged robot, most of the sensor readings are joint angles and velocities from the legs, which are not only numerically identically bounded but also change in similar patterns. The inclusion of previous actions gives each sensory neuron a chance to infer the casual relationship between the input channel and the applied actions, which helps with the input identification.

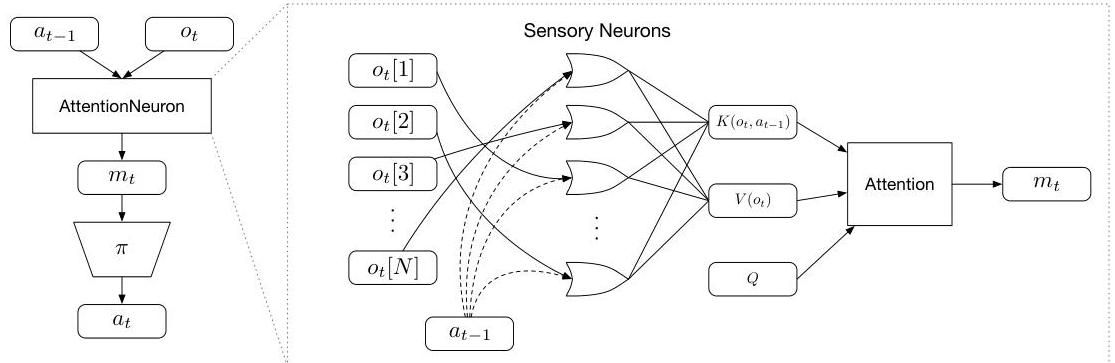
How AttentionNeuron works

The system splits the observation $o_t$ into N parts and processes them through independent sensory neurons that communicate via attention.

1. Input splitting:

• Continuous control: Each scalar becomes one input (e.g., Ant has 28 joint angles/velocities → 28 neurons)
• Vision: Image divided into 6×6 patches (e.g., 84×84 image → 196 patches → 196 neurons)

2. Per-neuron processing:
Each sensory neuron i receives:

• Its observation piece $o_t[i]$ (one scalar or one 6×6×4 patch)
• Previous action $a_{t-1}$ (shared across all neurons)

And computes:

• $f_k(o_t[i],a_{t-1})$: Temporal features via LSTM (for continuous) or frame differences (for vision)
• $f_v(o_t[i])$: Raw observation pass-through

3. Attention aggregation:
All neurons’ outputs are stacked:

$$K(o_t,a_{t-1})=\left[\begin{array}{c}{f}_k(o_t[1],a_{t-1})\\ ⋮\\ f_k(o_t[N],a_{t-1})\end{array}\right],V(o_t)=\left[\begin{array}{c}{f}_v(o_t[1])\\ ⋮\\ f_v(o_t[N])\end{array}\right]$$

Then attention computes:

$$m_t=\sigma \left(\frac{[Q{W}_q][K(o_t,a_{t-1})W_k{]}^T}{\sqrt{d_q}}\right)[V(o_t)W_v]$$

Where:

• $Q$: M learned query vectors (M=16 for CartPole, M=400 for Pong)
• $\sigma$: tanh (continuous control) or softmax (vision)
• $m_t$: Fixed-size output regardless of N inputs (M x output_dim)

If some neurons get noise/missing data, attention learns to ignore them. If neurons are shuffled, they re-identify their inputs within a few timesteps from temporal patterns.

Training with Evolution Strategies

Uses CMA-ES to optimize the entire system end-to-end. No individual neuron learning - the whole AttentionNeuron layer + policy network is treated as one black box and optimized based on episode rewards. ES handles the non-differentiable components and avoids gradient variance issues over long episodes.

How does this actually achieve permutation invariance?

Q is learned but not input-dependent (initialized from positional encodings), similar to the set transformer. K and V depend on the (permutable) inputs.
Permuting inputs only changes row order in K,V - but since attention computes weighted sums by
, the output $m_t$ stays the same regardless of input order.

Why is this system permutation invariant? Each sensory neuron is an identical neural network that is not confined to only process information from one particular sensory input. In fact, in our setup, the inputs to each sensory neuron are not defined. Instead, each neuron must figure out the meaning of its input signal by paying attention to the inputs received by the other sensory neurons, rather than explicitly assuming a fixed meaning. This encourages the agent to process the entire input as an unordered set, making the system to be permutation invariant to its inputs.

Not PI in the output space → Future Work: Still able to walk / move with one limb less / …

Connection to meta-learning

While not explicitly meta-learning, this work demonstrates that attention mechanisms can serve as adaptive weights similar to fast weights in meta-learning. The system exhibits rapid adaptation (within ~10 timesteps) through architectural bias alone - no meta-optimization across tasks or reward-based weight updates. It falls on the “black-box with parameter sharing” part of the meta-learning spectrum, showing that modular systems with shared parameters can achieve meta-learning-like behavior through self-organization. The permutation invariance essentially creates a distribution of tasks (all possible input permutations) that the system learns to handle simultaneously.

Future Work (copied)

An interesting future direction is to also make the action layer have the same properties, and model each motor neuron as a module connected using attention. With such methods, it may be possible to train an agent with an arbitrary number of legs, or control robots with different morphology using a single policy that is also provided with a reward signal as feedback. Moreover, our method accepts previous actions as a feedback signal in this work. However, the feedback signal is not restricted to the actions. We look forward to seeing future works that include signals such as environmental rewards to train permutation invariant meta-learning agents that can adapt to not only changes in the observed environment, but also to changes to itself.