binomial coefficient

Binomial Coefficient

The binomial coefficient $(k n)$ counts the number of ways to choose $k$ items from a set of $n$ items, where order doesn’t matter:
$(k n) = \frac{n \cdot ( n - 1 ) \cdot ( n - 2 ) \dots ( n - k + 1 )}{k !} = \frac{n !}{k ! ( n - k )!} = # permutations {0^{n - k}, 1^{k}}_{M}$
For $k < 0$ or $k > n$ , we define $(k n) = 0$ .

In set-theory terms, $(k n)$ is the number of subsets with $k$ elements of a set with size $n$ , or the number of permutations of the multiset ${0^{n - k}, 1^{k}}$ , so $(k n) \in N$

The denominator $k! (n - k)!$ accounts for the fact that we don't care about the order of selection.

The $k!$ term removes overcounting from different arrangements of the $k$ chosen items, while $(n - k)!$ does the same for the unchosen items, i.e. rearranging chosen or unchosen items doesn’t change the subset.

Fundamental Properties of Binomial Coefficients

$(0 n) = (n n) = 1$ since there’s exactly one way to choose no elements (empty set) or all elements.
$(k n) = (n - k n)$ due to symmetry - choosing $k$ items is equivalent to excluding $n - k$ items.
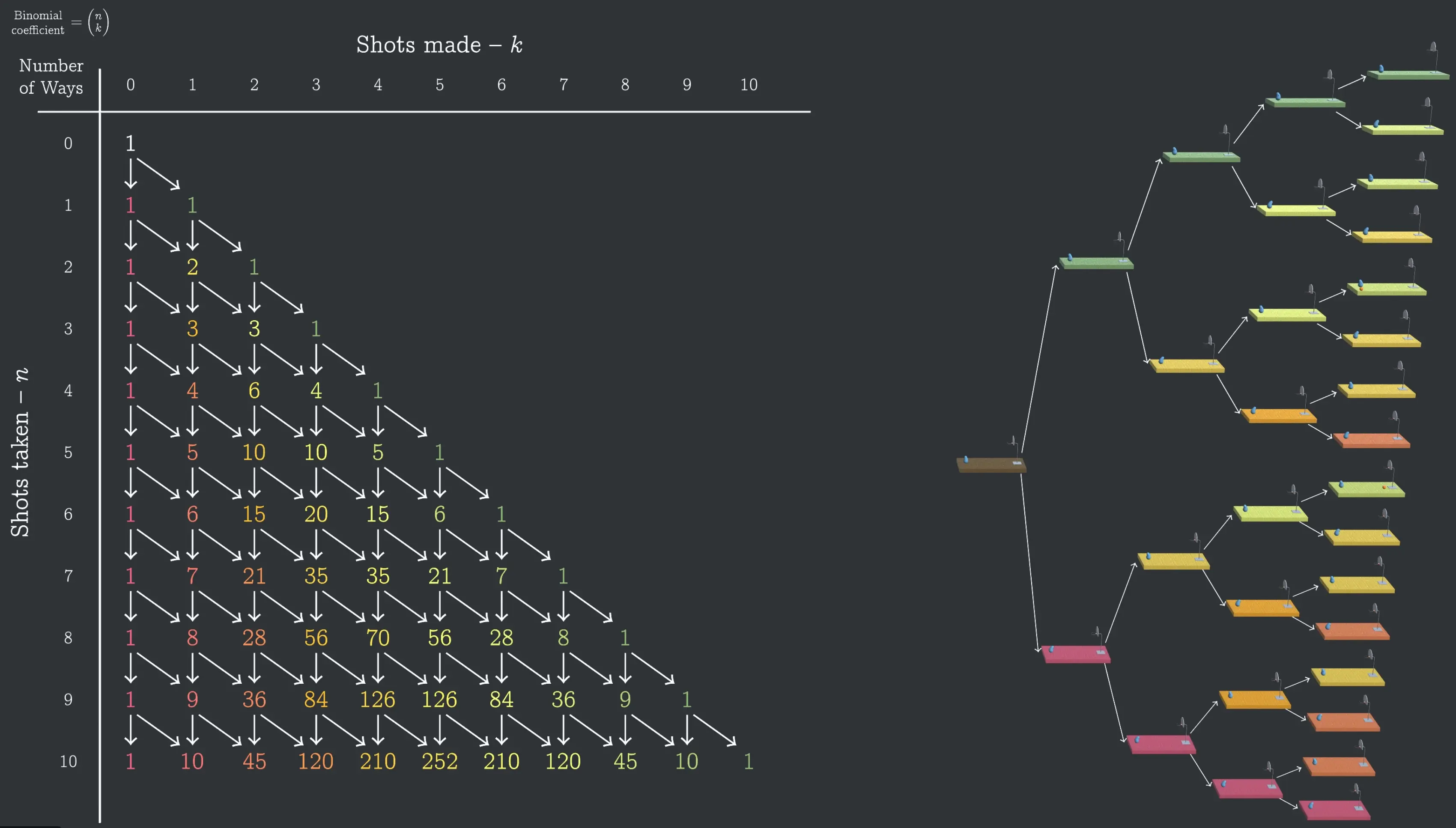
$(k n + 1) = (k - 1 n) + (k n)$ to choose $k$ from $n + 1$ items, we can ${include element (n + 1) : exclude element (n + 1) : choose k from n remaining choose (k + 1) from n remaining (k n) (k + 1 n)$ aka Pascal’s identity - also $(k n - 1) + (k - 1 n - 1) = (k n)$ (nice visual on the wiki).

The sum of all binomial coefficients for fixed $n$ (row of Pascal’s triangle) equals $2^{n}$

$k = 0 \sum n (k n) = 2^{n}$
This makes intuitive sense when thinking about sets: $(k n)$ counts the ways to choose $k$ items from $n$ items, and summing over all possible $k$ gives us the total number of possible subsets of an $n$ -element set, which is $2^{n}$ . Each element either is or isn’t in the subset, giving us two choices for each of the $n$ elements → power set.

Link to original

Binomial Theorem

For any $x, y \in C$ and $n \geq 0$ :
$(x + y)^{n} = k = 0 \sum n (k n) x^{n - k} y^{k}$
This generalizes the distributive law for exponents. The coefficients $(k n)$ appear in Pascal’s triangle, forming the coefficients in expansions of binomials like:
$(x + y)^{2} = (0 2) x^{2} + (1 2) x y + (2 2) y^{2} = x^{2} + 2 x y + y^{2}$
With negative terms, the $(- 1)^{k}$ factor creates alternating signs:
$(x - y)^{n} = k = 0 \sum n (k n) x^{n - k} (- y)^{k} = k = 0 \sum n (k n) (- 1)^{k} x^{n - k} y^{k}$ $(x - y)^{2} = (0 2) x^{2} - (1 2) x y + (2 2) y^{2} = x^{2} - 2 x y + y^{2}$

Circular transclusion detected: general/Pascal's-triangle

Info

$x^{2} - y^{2} = (x - y) (x + y)$
$x^{3} + y^{3} = (x + y) (x^{2} - x y + y^{2})$
$x^{3} - y^{3} = (x - y) (x^{2} + x y + y^{2})$

References

factorial

Max Wolf's Second Brain

Explorer

binomial coefficient

References

Graph View

Backlinks