binomial distribution

Binomial Distribution

The binomial distribution with parameters $n$ (number of trials) and $p$ (probability of success on each trial) is a discrete probability distribution that describes the number of successes $k$ in a sequence of $n$ independent bernoulli experiments. Its PMF is given by

$$P(X=k;n,p)=\left(\genfrac{}{}{0ex}{}{n}{k}\right)\cdot p^k\cdot (1-p{)}^{n-k}\text{for }0\le k\le n$$

$n\dots$ total number of Bernoulli events
$k\dots$ number of “positive” events
$p\dots$ probability of positive event
$\left(\genfrac{}{}{0ex}{}{n}{k}\right)\dots$ binomial coefficient – number of ways to choose $k$ successes from $n$ trials

Binomial random variable

A random variable $X$ that counts the number of successes in $n$ independent Bernoulli trials, each with probability of success $p$, is called a binomial random variable:
When we write $X\sim \text{binomial}(n,p)$, it implies that the probability of $X$ taking the value $k$ is given by the PMF of the binomial distribution.

EXAMPLE

$n=2$
$P(X=0)=P(F_1{F}_2)=P(F_1)P(F_2)=(1-p{)}^2$
$P(X=1)=P(S_1{F}_2)+P(F_1{S}_2)=P(S_1)P(F_2)+P(F_1)P(S_2)=2p(1-p)$
$P(X=2)=P(S_1{S}_2)=P(S_1)P(S_2)=p^2$
We can pull them apart because they are independent.
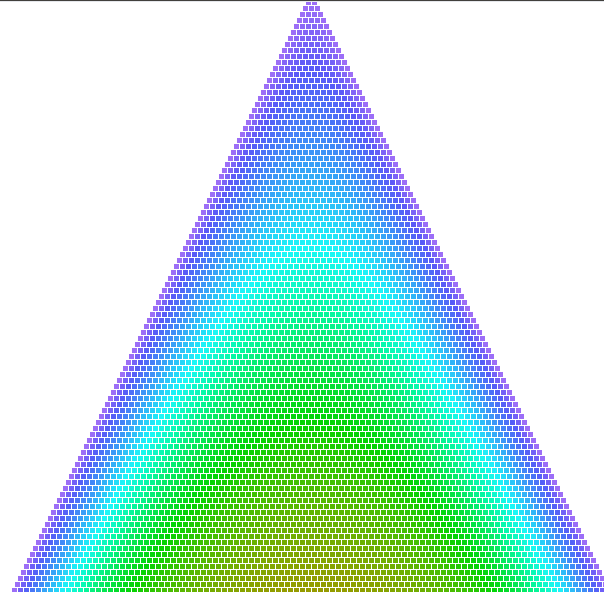
Note: The coefficients are $\left(\genfrac{}{}{0ex}{}{2}{0}\right)=1,\left(\genfrac{}{}{0ex}{}{2}{1}\right)=2,\left(\genfrac{}{}{0ex}{}{2}{2}\right)=1$

Pascals triangle (the binomial distribution) converges to the normal distribution for large $n$.

At about $n=30$, the normal distribution starts to be a very good approximation.

Computing $\mathcal{N}(\mu ,{\sigma }^2)$ is easier than computing the binomial distribution. Flipping a coin 400 times: calculating $P(190\le X\le 230)$ requires summing 41 binomial terms:

$$P(X=k)=\left(\genfrac{}{}{0ex}{}{400}{k}\right)(0.5{)}^k(0.5{)}^{400-k}\text{ for }k\in \{190,...,230\}$$

With normal approximation: $X\sim \mathcal{N}(200,10)$

$$P(190\le X\le 230)\approx 85\%$$

$$\begin{array}{rlr}X\sim \text{binomial}(n,p)& \to X\sim \text{normal}(np,\sqrt{npq})& \text{if }npq\text{ is not too small}\\ & \to X\sim \text{poisson}(\lambda )& \text{if }np\text{ or }nq\text{ is small}\end{array}$$

where $p$ is the probability of success, $q=1-p$ is the probability of failure, and $n$ is the number of trials.
This is true $npq$ is not too small, i.e. success and failure are not too rare.
If they are, the binomial distribution converges to the poisson distribution, where $\lambda =np$ is the average number of successes.

See also Central Limit Theorem.

Link to original

References

3b1b, primer