evolution strategies

Evolution Strategies (ES)

ES are a class of evolutionary optimization algorithms for continuous, gradient-free parameter optimization.

There is no one definition, but broadly:

ES is an algorithm that provides the user a set of candidate solutions to evaluate a problem. The evaluation is based on an objective function that takes a given solution and returns a single fitness value. Based on the fitness results of the current solutions, the algorithm will then produce the next generation of candidate solutions that is more likely to produce even better results than the current generation. The iterative process will stop once the best known solution is satisfactory for the user. ¹

In a nutshell:
ES maintain a probability distribution (typically gaussian) over the parameter space:

1. Sample population: ${\theta }_i\sim \mathcal{N}(\mu ,{\sigma }^2)$

2. Evaluate fitness: $f({\theta }_i)$

3. Update distribution parameters based on fitness, repeat.

   Unlike GA which uses discrete representations with crossover, ES operates directly on real-valued vectors and is mutation-driven.

Variants

cma-es
natural evolution strategies
OpenAI-ES

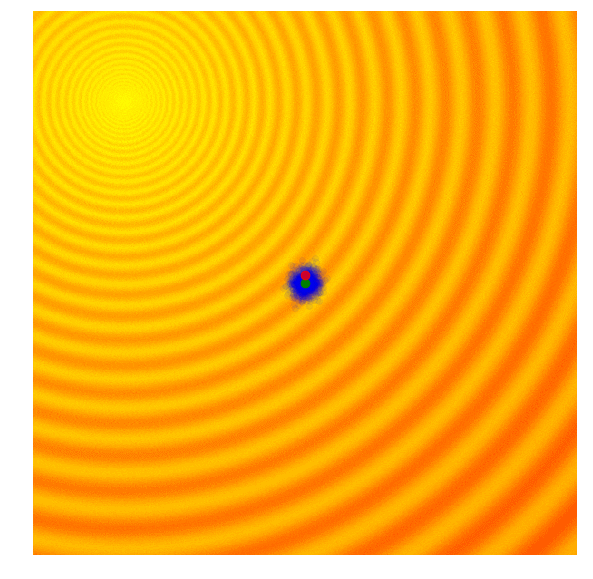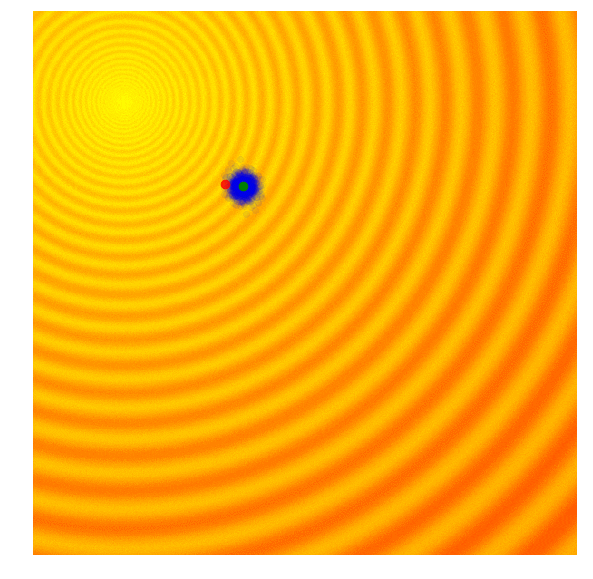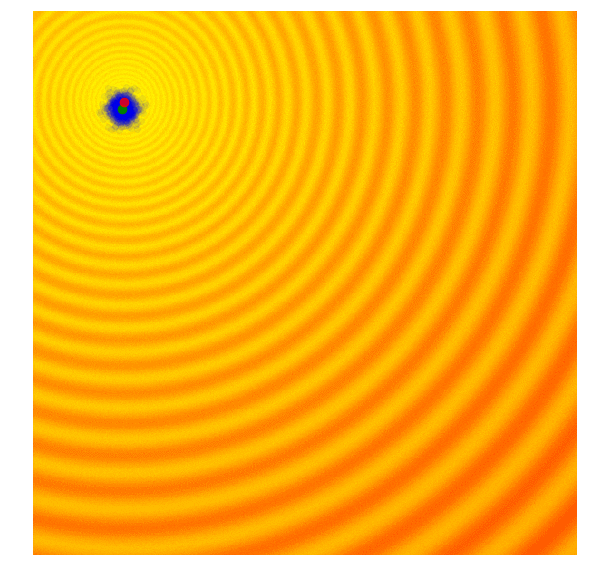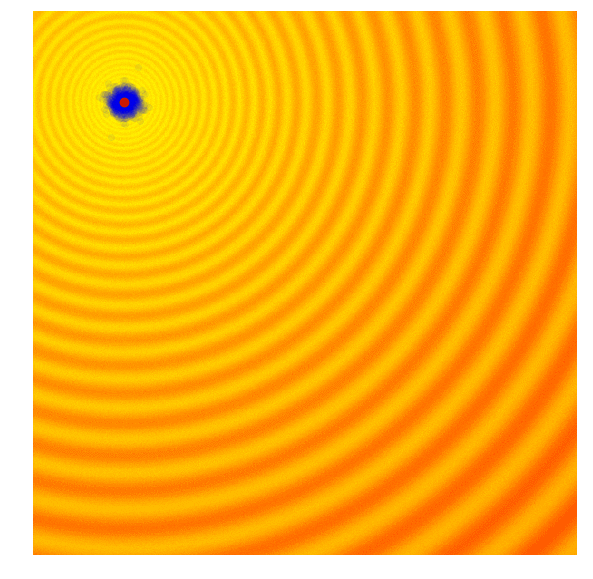
Simple ES

The simplest form of an evolution strategy is just iteratively updating the mean of the sampling distribution (green) to the best solution of the current population (red). This only works on toy problems.

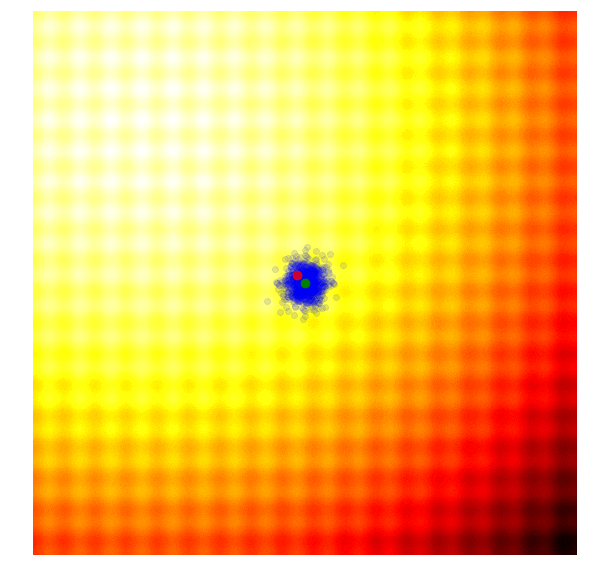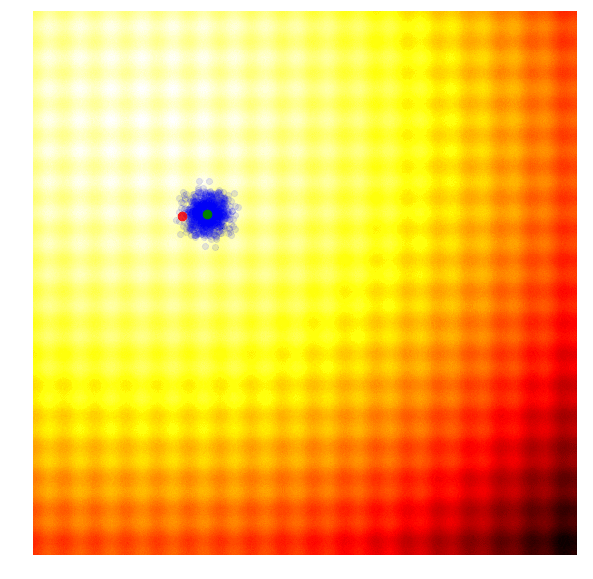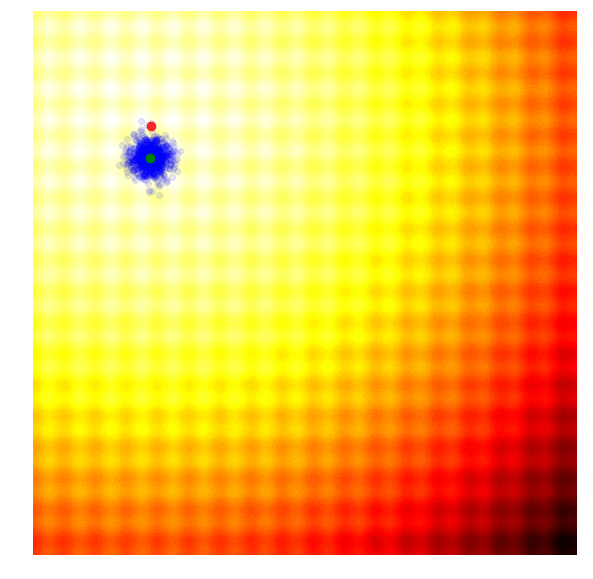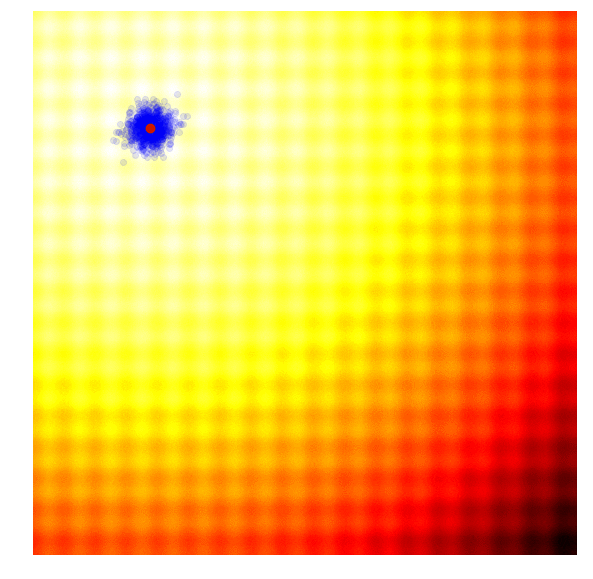
Selection in ES $(\mu +\lambda )$, $(\mu ,\lambda )$

$\mu$ … elites, best performing individuals of a generation
$\lambda$ … population size (including elites)
$(\mu +\lambda )$ … give the parents a chance to compete with their children (elitist, best survive)
$(\mu ,\lambda )$ … replace parents by children (can help overcome local optimium through turnover/diversity→ advantage over gradient-based methods; bio inspo: death of old age)

Why isn't everyone using ES?

Max Wolf — 16/11/2024, 18:21
Hi, so I recently came across this paper [Evolution Strategies as a Scalable Alternative to Reinforcement Learning](https://arxiv.org/abs/1703.03864) and I was wondering why is nobody using this method of optimization (at least in RL), considering all the benefits they list: no backprop, robust against exploding gradients, allowing non-differentiable elemtents, better with long-horizon / long-lasting action effect problems, invariant to frequency at which the agent acts, suitable if no good value function is available, [works well with sparse rewards](https://arxiv.org/abs/2205.07592), ...... which basically sounds like most taks that are not games or toy problems?
For example I found that [VSML](https://arxiv.org/abs/2012.14905) uses ES as it enables longer training horizons and more stable optimization. One reason why they can successfully use it is their small parameter space.
Am I missing something that's really hindering this algorithm from broader use or is it just that the types of problems that are currently being researched have no use for it's benefits? (with downsides being sample efficiency and parameter scaling)

clembonnet — 19/11/2024, 15:21
My take on it is that ES are zero-order gradient objective optimization methods. You climb your objective using zero-order information only (no gradients).
First-order optimization methods use gradients of your objective to climb it.
Both are possible, and they may each work better in different situations.
For instance, if you have two unbiased estimators of your objective gradient, the best method will be the one with lower variance. In this case, it can be linked to how smooth your objective is. If it isn’t smooth (high lipschitz constant), then you will have lower variance with ES, if it is relatively smooth (low lipschitz), using gradients is better.
I can refer you to Mohamed et al, 2019: https://arxiv.org/abs/1906.10652
Hope this helps!

clembonnet — 19/11/2024, 15:23
Draw a 1D convex curve (e.g square function) and add some high frequency fluctuations to it, e.g. x^2 + 0.1 sin(100*x)
With the sinus (high lipschitz), you would rather use ES (to smoothen the objective), but without the sinus (low lipschitz), you’ll get much quicker convergence using gradients.

Right, because most real-world objectives are totally smooth + we have good gradients for them…
→

If you have access to gradients/good proxy gradients, i.e. you can do supervised learning, ES’s computational overhead isn’t worth it. But in RL, gradients are noisy anyway, and ES can reduce that noise by adding more offspring (parallelizable). ES is competitive when domain noise degrades SGD’s gradient quality enough that ES’s approximation isn’t much worse.

Link to original

→ What really held it back was just the perception of it being less scalable, even though ES are much more bitter lesson-pilled, and superior in many respects, as shown by Evolution Strategies at Scale - LLM Fine-Tuning Beyond Reinforcement Learning and Evolution Strategies at the Hyperscale.

In my book, what makes the most sense is to always use ES, combine it with pretrained models, or use gradients for self-supervised / predictive tasks (much like Recurrent World Models Facilitate Policy Evolution did).

References

https://lilianweng.github.io/posts/2019-09-05-evolution-strategies/

Footnotes

1. Highly recommended blog: https://blog.otoro.net/2017/10/29/visual-evolution-strategies ↩