monte carlo tree search is basically smartly depth limited breadth search - “best-first search”.
So you descend the tree, exploring the nodes which are more promising (by your metric) but not having to continue on unpromising paths, the only condition being, that if you want to go deeper on one node, you need to have looked at all of its siblings at least once.
One approximation for how good a node is e.g. how many times you won relative to the number of times you visited the node.
The details of how MCTS is implemented varies quite a bit, but it generally follows the following steps:
the steps
For game state , we store:
# games played involving
# games won (by player ) that involved
we want to explore the paths where we are most confident that they will lead to victory but also still explore:
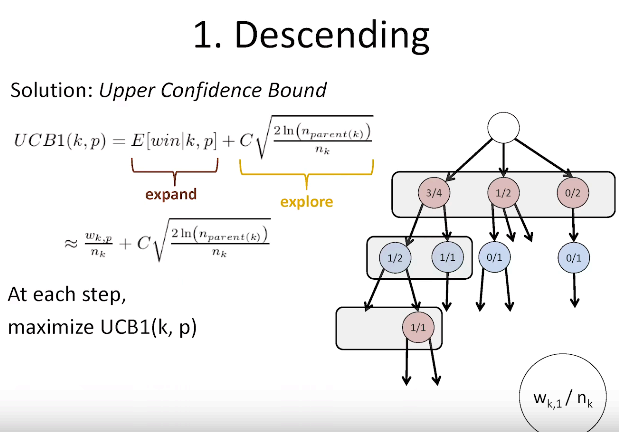
The exploration term is higher for nodes () visited fewer times () relative to their parent’s visits (), encouraging a wider search.
ensures that the desire to explore children grows as the parent node is visited more, but at a diminishing rate.
is prlly related to standard error confidence interval scaling.
See upper confidence bound for more notes.
The winning confidence for node can be approximated to be the number of winning trajectories involving divided by the number of trajectories involving .
For expanding the tree, we just create a new node with initial values:
To get to an end state, we can just play random moves until the end:

If you have an inexpensive way of evaluating moves, then you can also use that instead of random, but caution should be exercised, since exploration is more valuable than the simulations + if you use heuristics, they might fail in complex scenarios where random sim wouldn’t.
Note
We usually do not store infos into the intermediate randomly chosen nodes, we only want to know whether node lead to win/lose via some randomly chosen path (we don’t want to influence the actual MC exploration, even if we’d get slight perf. improvements).
Another option is also to estimate the end with an ANN.
Once we obtained a new end state for the newly generated node, we update the and values of the nodes:

NOTE: The of the highlighted blue node should be .
Now you run steps 1-4 a whole bunch of times and terminate the search at any time you want. Then, the trivial way to pick the “best” node is to return the highest ranking first ancestor (expected win rate):
However, this has the lmitation that one state might be way superior, but due to the randomness of the search, a lot of paths have also ended up in poor directions (whereas a less explored node might be lucky and have a temporarily higher rating), hence we intrudoce the additional criterion, that it needs to be the highest expected win rate, while also being the most visited node for us to be able to terminate (can’t terminate at any time anymore).
General Pros:
- handles large branching factor (growing tree asymmetrically, balancing expansion and explorat.)
- terminate any time
- trivially parallelizable
- don’t need heuristics
- complete: guaranteed to find a solution with enough time
General Cons:
- not good for extreme tree depths (as the number of moves increases, correlation of play-state and whether a random play-out would suggest that you are in a good or a bad situation)
- MCTS is not about a long term policy but the next sequence of moves that you should make!
- simulation has to be quick and easy
- random play should be “weakly correlated” with the quality of the game state (this means that the outcomes of random simulations provide some indication about the state’s quality, but they are not definitive or strongly predictive??)
Link to original“ MCTS” in muzero neither does random simulation nor does it rollout till the end.
References
OCW Advanced 4. Monte Carlo Tree Search
https://github.com/petosa/multiplayer-alphazero/blob/master/mcts.py