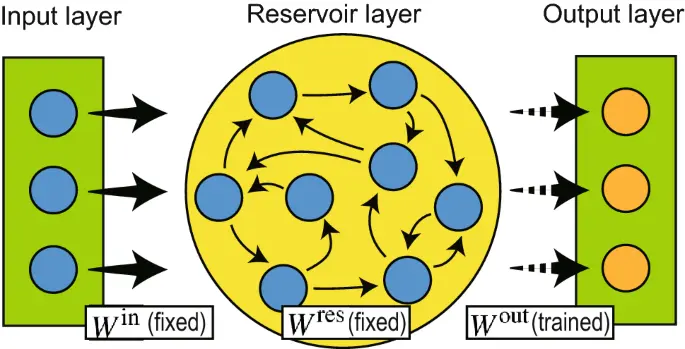
Reservoir computing
In 2001 a fundamentally new approach to RNN design and training was proposed independently by Wolfgang Maass under the name of liquid state machines and by Herbert Jaeger under the name of echo state networks. This approach is now often referred to as the Reservoir Computing Paradigm.
Reservoir computing also has predecessors in computational neuroscience (see Peter Dominey’s work in section 3.1) and in machine learning as the Backpropagation-Decorrelation learning rule proposed by Schiller and Steil in 2005. As Schiller and Steil noticed, when applying BPTT training to RNNs the dominant change appear in the weights of the output layer, while the weights of the deeper layer converge slowly.
It is this observation that motivates the fundamental idea of Reservoir Computing: if only the changes in the output layer weights are significant, then the treatment of the weights of the inner network can be completely separated from the treatment the output layer weights.
Echo State Property (ESP)
The Echo State Property is a fundamental requirement for reservoir networks to function properly. It states that the effect of previous states and inputs on future states should gradually diminish over time, rather than persisting indefinitely or becoming amplified.
In mathematical terms, the ESP ensures that the network “forgets” initial conditions and depends only on recent inputs after sufficient time has passed. This creates a form of fading memory that allows the reservoir to maintain useful information about recent inputs while discarding older, less relevant information.
For practical applications, the ESP can be ensured by scaling the reservoir weight matrix W so that its spectral radius is less than or equal to 1. This prevents the recursive dynamics from exploding.
The spectral radius serves as a rough indicator of the reservoir’s memory capacity:
- Values close to 0: Very short memory (quickly forgets previous inputs)
- Values close to 1: Longer memory (retains information about inputs for more timesteps)
- Values greater than 1: Risk losing the ESP, leading to chaotic or unstable behavior
To test a reservoir’s memory capacity practically, we can see if the system can recreate an input with a k-step delay. The maximum k for which the reservoir can still accurately reproduce the input provides a measure of its effective memory span.
Separability Property
The separability property refers to a reservoir’s ability to distinguish between different input patterns. This is essential for classification and prediction tasks, as different inputs should produce distinguishably different states within the reservoir.
A good reservoir network should map similar inputs to similar states while mapping dissimilar inputs to dissimilar states, creating representations that preserve the important distinctions in the input space.
A practical heuristic to measure separability is to compute the distance between different reservoir states caused by different input sequences. The greater these distances, the better the reservoir’s separability.
Two effective methods to improve separability:
- Make the connection matrix sparse (many zero weights), which helps decouple the activation signals within the network
- Use larger networks with more neurons, which provide more varied activations and greater representational capacity
Topology
The arrangement of neurons within the reservoir (its topology) significantly affects performance, but finding the optimal topology remains an open question in reservoir computing.
Larger networks with more neurons generally provide better performance, as they offer finer-grained classification capabilities and higher separability. However, there’s substantial variation in performance even among randomly created reservoirs with the same size.
While sparse connection matrices generally work better than fully connected ones, research comparing different topologies (scale-free, small-world, biologically inspired) found no clear winner that consistently outperforms simple random networks across all tasks.
The performance variation among random networks with the same parameters suggests that topology optimization approaches may be valuable, even though no universal “best topology” has been identified.