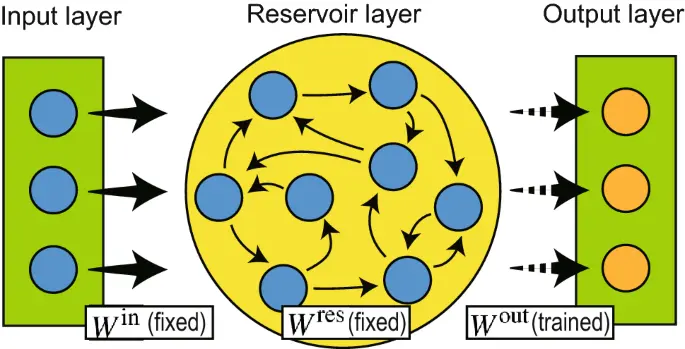
LSMs are a type of reservoir computing:
Link to originalReservoir computing
In 2001 a fundamentally new approach to RNN design and training was proposed independently by Wolfgang Maass under the name of liquid state machines and by Herbert Jaeger under the name of echo state networks. This approach is now often referred to as the Reservoir Computing Paradigm.
Reservoir computing also has predecessors in computational neuroscience (see Peter Dominey’s work in section 3.1) and in machine learning as the Backpropagation-Decorrelation learning rule proposed by Schiller and Steil in 2005. As Schiller and Steil noticed, when applying BPTT training to RNNs the dominant change appear in the weights of the output layer, while the weights of the deeper layer converge slowly.
It is this observation that motivates the fundamental idea of Reservoir Computing: if only the changes in the output layer weights are significant, then the treatment of the weights of the inner network can be completely separated from the treatment the output layer weights.
Liquid State Machines (LSMs) are the other pioneer method of reservoir computing, developed simultaneously and independently from echo state network, by Wolfgang Maass.
Coming from a computational neuroscience background, LSMs use more biologically realistic models of spiking integrate-and-fire neurons and dynamic synaptic connection models, in order to understand the computing power of real neural circuits. As such LSMs also use biologically inspired topologies for neuron connections in the reservoir, in contrast to the randomized connections of ESNs. However, creating a network that mimics the architecture of the cerebral cortex requires some engineering of the weight matrix; and simulating spiking neurons, which are dynamical systems themselves in which electric potential accumulates until it fires leaving a trail of activity bursts, is slow and computationally intensive.
Both these facts make the LSM method of reservoir computing more complicated in their implementation and have not commonly been used for engineering purposes.
Link to originalLSMs, their limitations, and the critical state
LSMs avoid training via backpropagation by using a sparse, recurrent, spiking neural network (liquid) with fixed synaptic connection weights to project inputs into a high dimensional space from which a single neural layer can learn the correct outputs. Yet, these advantages over deep networks come at the expense of 1) sub-par accuracy and 2) extensive data-specific hand-tuning of liquid weights. Interestingly, these two limitations have been targeted by several studies that tackle one or the other, but not both.
As a general heuristic, LSM accuracy is maximized when LSM dynamics are positioned at the edge-of-chaos and specifically in the vicinity of a critical phase transition that separates: 1) the sub-critical phase, where network activity decays, and 2) the super-critical (chaotic) phase, where network activity gets exponentially amplified. Strikingly, brain networks have also been found to operate near a critical phase transition that is modeled as a branching process. Current LSM tuning methods organize network dynamics at the critical branching factor by adding forward and backward communication channels on top of the liquid. This, however, results in significant increases in training complexity and violates the LSM’s brain-inspired self-organization principles. For example, these methods lack local plasticity rules that are widely observed in the brain and considered a key component for both biological and neuromorphic learning.
A particular local learning rule, spike-timing dependent plasticity (STDP), is known to improve LSM accuracy. Yet, current methods of incorporating STDP into LSMs further exacerbate the limitations of data-specific hand-tuning as they require additional mechanisms to compensate for the STDP-imposed saturation of synaptic weights. This signifies the scarcity of LSM tuning
methods that are both computationally efficient and data-independent.