Multi-Agent Reinforcement Learning is a Sequence Modeling Problem

year: 2022/05
paper: https://arxiv.org/abs/2205.14953
website: https://www.reddit.com/r/MachineLearning/comments/v2af3k/r_multiagent_reinforcement_learning_can_now_be/ | https://sites.google.com/view/multi-agent-transformer
code: https://github.com/PKU-MARL/Multi-Agent-Transformer
connections: MARL, transformer

---

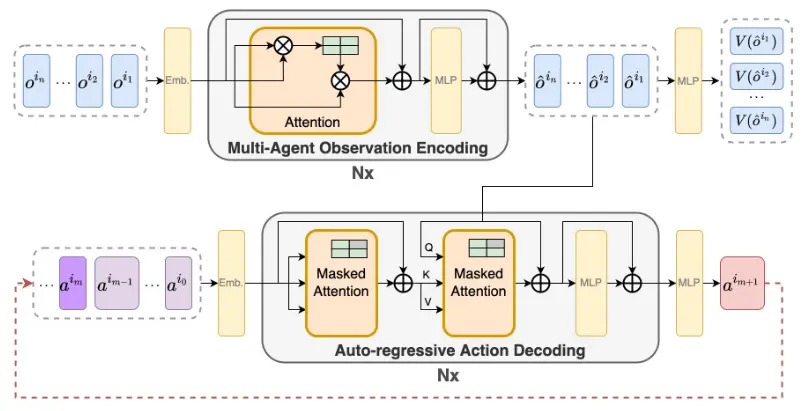
Note how Q comes from the encoder, which is a non-standard way to do cross-attention.
There are no notes about any architectural details in the paper, though maybe this inversion shifts focus from “what context is relevant for the next token?” (NLP) to “what action should follow given the global state and prior actions?” (MARL).

Preliminaries

Multi-Agent Observation-Value Functions

The multi-agent observation-value function $Q_{\pi }^{i_{1:m}}(o,a^{i_{1:m}})$ measures the expected return starting from observation $o$ when a subset of agents $i_{1:m}$ execute specified actions $a^{i_{1:m}}$ and all other agents execute actions according to their current policy $\pi$.
Building on this, for disjoint ordered subsets of agents $i_{1:m}$ and $j_{1:h}$, the multi-agent advantage function measures the relative benefit of agents $i_{1:m}$ taking specific actions $a^{i_{1:m}}$ after agents $j_{1:h}$ have committed to actions $a^{j_{1:h}}$:

$$A_{\pi }^{i_{1:m}}(o,a^{j_{1:h}},a^{i_{1:m}})=Q_{\pi }^{j_{1:h},i_{1:m}}(o,a^{j_{1:h}},a^{i_{1:m}})-Q_{\pi }^{j_{1:h}}(o,a^{j_{1:h}})$$

The advantage is positive if the chosen actions $a^{i_{1:m}}$ lead to better expected returns than letting those agents follow their default policy behavior, given the actions already chosen by agents $j_{1:h}$.

Example

Consider a team of 3 agents where:
Agent 1 commits to action $a^1$ first ($j_{1:h}=\{1\}$) and we want to evaluate the advantage of agents 2 and 3’s joint action $(a^2,a^3)$ ($i_{1:m}=\{2,3\}$)
The advantage function would measure how much better/worse agents 2 and 3’s chosen actions are compared to the expected value after only agent 1’s action and following the policy of agents 2 and 3.

Multi-Agent Advantage Decomposition Theorem

Let $i_{1:n}$ be a permutation of agents. For any joint observation $o$ and joint action $a$:

$$A_{\pi }^{i_{1:n}}(o,a^{i_{1:n}})=\sum _{m=1}^n{A}_{\pi }^{i_m}(o,a^{i_{1:m-1}},a^{i_m})$$

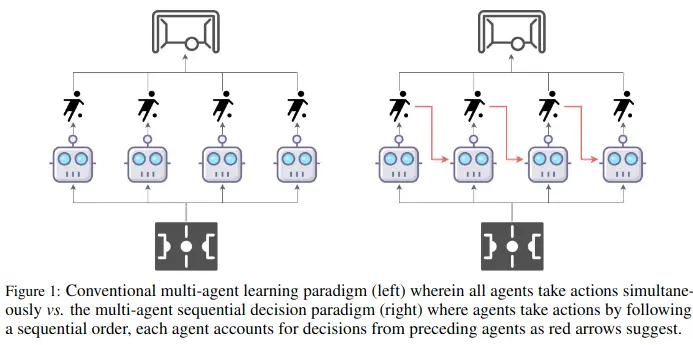
The total advantage of a joint action can be decomposed into a sum of individual advantages, where each agent’s advantage is conditioned on the actions chosen by previous agents in the permutation.

This enables sequential decision making.

Agent $i_1$ goes first, picks an action with $a^{i_1}$ aiming for positive advantage $A_{\pi }^{i_1}(o,a^{i_1})>0$
Agent $i_2$, knowing $a^{i_1}$, chooses $a^{i_2}$ for positive $A_{\pi }^{i_2}(o,a^{i_1},a^{i_2})>0$
Agent $i_3$, knowing $(a^{i_1},a^{i_2})$, …

Instead of searching the entire joint action space ${\prod }_{i=1}^n|A^i|$, we can search each agent’s action space separately ${\sum }_{i=1}^n|A^i|$.
→ Each agent can make decisions based information about what others have done, incrementally improving actions.
→ The computational savings get more dramatic as you add more agents

Link to original

MAPPO objective

The objective of MAPPO is equivalent to that of PPO, but equipping each agent with one shared set of parameters, i.e. ${\theta }^i={\theta }^j,\forall i,j\in \mathcal{N}=\{1,\dots n\}$. It uses the agent’s combined trajectories for the shared policy’s update.
So the objective for optimizing the policy parameters ${\theta }_{k+1}$ at iteration $k+1$ is:

$$\sum _{i=1}^n{\mathbb{E}}_{\mathbf{o}\sim {\pi }_{{\theta }_k},\mathbf{a}\sim {\pi }_{{\theta }_k}}\left[\min \left(\frac{{\pi }_{\theta }({\mathbf{a}}^i|\mathbf{o})}{{\pi }_{{\theta }_k}({\mathbf{a}}^i|\mathbf{o})}{A}_{{\pi }_{{\theta }_k}}(\mathbf{o},\mathbf{a}),\text{clip}\left(\frac{{\pi }_{\theta }({\mathbf{a}}^i|\mathbf{o})}{{\pi }_{{\theta }_k}({\mathbf{a}}^i|\mathbf{o})},1\pm ϵ\right)A_{{\pi }_{{\theta }_k}}(\mathbf{o},\mathbf{a})\right)\right]$$

The constraint on the joint policy space imposed by shared parameters can lead to an exponentially-worse sub-optimal outcome (details; page 4).

Link to original

HAPPO vs MAPPO

MAPPO is a straightforward application of PPO to multi-agent settings, often forcing all agents to share one set of policy parameters. This can be suboptimal when agents need different behaviors.
HAPPO relaxes this constraint by:

1. Sequentially updating each agent in a random permutation $i_1,\dots ,i_n$, where agent $i_m$ updates using the newly updated policies of agents $i_{1:m-1}$.
2. Leveraging the Multi-Agent Advantage Decomposition Theorem, which yields a valid trust‐region update for each agent’s local advantage $A_{\pi }^{i_m}(o,a^{i_{1:m-1}},a^{i_m})$. Specifically, HAPPO applies the standard PPO (clipped) objective to each agent while treating previously updated agents’ policies as “fixed.” Because the decomposition theorem ensures the local advantage aligns with the global return, any PPO‐style step that respects the trust region (i.e., doesn’t deviate too far from the old policy) guarantees a monotonic improvement for the entire multi-agent policy.
3. Maintaining distinct policy parameters for truly heterogeneous capabilities.

This ensures a monotonic improvement guarantee for the joint return – something MAPPO’s parameter-sharing approach can’t guarantee. As a result, HAPPO typically performs better than MAPPO in scenarios where agents must learn different skillsets.
However, one drawback of HAPPO is that agent’s policies has to follow the sequential update scheme (in the permutation), thus it cannot be run in parallel.

Link to original

Implementation

Algorithm

Steps:

1. Generate encoded joint agents observations: $\hat{O}=\psi (O)$
2. Generate state-value estimates from observations: $V(O)=\text{MLP}(V(\hat{O}))$
3. Autoregressively decode agent actions, while cross-attending the encoded observations: $a^{i_{m+1}}=\theta (a^{i_{0:m}})$

Slap PPO on top… that’s it!