fourier series

We can represent a function $f(x)$ as a sum of cosines and sines of increasingly high frequency:

$$f(x)=\frac{A_0}{2}\sum _{k=1}^{\infty }(A_k\cos (kx)+B_k\sin (kx))$$ $$A_k=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)\cos (kx)dx=\frac{1}{\Vert \cos (kx){\Vert }^2}⟨f,\cos (kx)⟩$$ $$B_k=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)\sin (kx)dx=\frac{1}{\Vert \sin (kx){\Vert }^2}⟨f,\sin (kx)⟩$$

The coefficients $A_k$ and $B_k$ are found by projecting ¹ $f(x)$ onto the basis functions $\cos (kx)$ and $\sin (kx)$ by computing the inner product between $f(x)$ and each basis function. ²
This works because the set of functions $\{\cos (kx),\sin (kx){\}}_{k=0}^{\infty }$ form an orthonormal basis for the space of periodic functions with period $2\pi$, after we normalize them.

In the above example, $f(x)$ is assumed to be periodic with period $2\pi$.
For a function with period $L$ ³, we can scale the basis functions accordingly ⁴:

$$f(x)=\frac{A_0}{2}+\sum _{k=1}^{\infty }\left(A_k\cos \left(\frac{2\pi kx}{L}\right)+B_k\sin \left(\frac{2\pi kx}{L}\right)\right)$$ $$A_k=\frac{2}{L}{\int }_0^{L}f(x)\cos \left(\frac{2\pi kx}{L}\right)dx$$ $$B_k=\frac{2}{L}{\int }_0^{L}f(x)\sin \left(\frac{2\pi kx}{L}\right)dx$$

If the function is not periodic, we can still use Fourier series to approximate it over a finite interval by treating the interval as one period of a periodic function (the fourier series will just keep repeating it).

fourier analysis
approximation

Footnotes

1. Vector decomposition via projection

   Any vector $\mathbf{v}$ can be decomposed relative to a direction $\mathbf{u}$:

   $$\mathbf{v}={\mathbf{v}}_{\parallel }+{\mathbf{v}}_{\perp }$$

   where ${\mathbf{v}}_{\parallel }$ points along $\mathbf{u}$ and ${\mathbf{v}}_{\perp }$ is orthogonal to it.

   The projection ${\mathbf{v}}_{\parallel }={\text{proj}}_{\mathbf{u}}(\mathbf{v})$ is the foot of the perpendicular from $\mathbf{v}$ to $\text{span}\{\mathbf{u}\}$. The perpendicular component is:

   $${\mathbf{v}}_{\perp }=\mathbf{v}-{\mathbf{v}}_{\parallel }$$

   The inner product $⟨\mathbf{v},\mathbf{u}⟩$ measures how much $\mathbf{v}$ points along $\mathbf{u}$. Scaling by $1/\Vert \mathbf{u}{\Vert }^2$ gives the right coefficient:

   $${\text{proj}}_{\mathbf{u}}(\mathbf{v})=\frac{⟨\mathbf{v},\mathbf{u}⟩}{\Vert \mathbf{u}{\Vert }^2}\mathbf{u}$$

   If $\mathbf{u}$ is already a unit vector, this simplifies:

   $${\text{proj}}_{\hat{\mathbf{u}}}(\mathbf{v})=⟨\mathbf{v},\hat{\mathbf{u}}⟩\hat{\mathbf{u}}$$

   ---

   For orthogonal basis vectors, any vector decomposes into projections onto each basis direction. Same vector $\mathbf{v}$ in different bases $\{{\mathbf{b}}_1,{\mathbf{b}}_2\}$ or $\{{\mathbf{c}}_1,{\mathbf{c}}_2\}$:

   $$\mathbf{v}=\frac{⟨\mathbf{v},{\mathbf{b}}_1⟩}{\Vert {\mathbf{b}}_1{\Vert }^2}{\mathbf{b}}_1+\frac{⟨\mathbf{v},{\mathbf{b}}_2⟩}{\Vert {\mathbf{b}}_2{\Vert }^2}{\mathbf{b}}_2\mathbf{v}=\frac{⟨\mathbf{v},{\mathbf{c}}_1⟩}{\Vert {\mathbf{c}}_1{\Vert }^2}{\mathbf{c}}_1+\frac{⟨\mathbf{v},{\mathbf{c}}_2⟩}{\Vert {\mathbf{c}}_2{\Vert }^2}{\mathbf{c}}_2$$

   Each coefficient tells you how much of that basis vector appears in $\mathbf{v}$.

   Link to original

   ↩

2. Inner Product of two functions

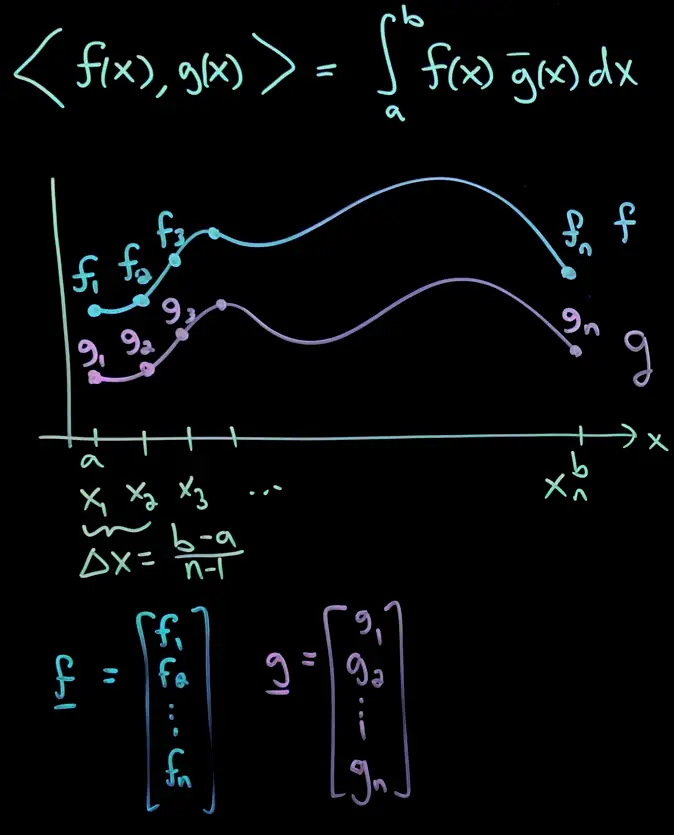
   For two functions on the interval $[a,b]$, the $L^2$ inner product is defined as:

   $$⟨f,g⟩={\int }_a^{b}f(x)\overline{g(x)}dx$$

   It has all the same properties as any inner product, and tells you how aligned two functions are.
   The bar denotes the complex conjugate, so $⟨f,f⟩={\int }_a^b|f(x){|}^{2}dx\ge 0$ (positive definiteness).
   For real-valued functions, the bar can be omitted.

   This can be thought of taking the dot product of two vectors with infinitely many components, one at each $x$ in the interval, or rather it is just the Riemann approximation: $⟨f,g⟩={\lim }_{n\to \infty }{\sum }_{i}f(x_i)\overline{g(x_i)}\Delta x$.
   

   Link to original

   ↩

3. formally, $f(x)\in L_2([0,L)];\mathbb{C})$, meaning it is in the hilbert space of square integrable functions over the interval $[0,L]$, i.e. has a bounded integral of its square over that interval, i.e. the integral ${\int }_0^L|f(x){|}^{2}dx<\infty$ ↩

4. Transclude of trigonometric-function#^7d381d

   ↩