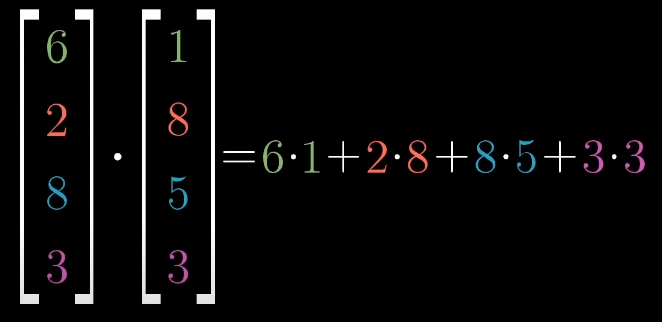dot product

Dot product

$$a\cdot b=a_1{b}_1+\text{... }+a_n{b}_n$$

equivalent to:

$$a\cdot b=||a||||b||cos(\theta )$$

$\theta$ … angle between $a$ and $b$

The dot product is the unnormalized version of cosine similarity (equivalent up to scale).
It measures how parallel two vectors are. As opposed to the cross product, which measures how perpendicular two vectors are.

Notation: $a\cdot b=⟨a,b⟩$

$\sqrt{a\cdot a}=||a||$

The dot product measures the similarity/overlap between two vectors.

Naturally, it shows up everywhere you have similarity-weighted readouts, like associative memory.
It also shows up every time a neuron computes a weighted sum of its inputs $y=w^{T}x$, which leads to the interpretation of neurons as feature detectors, i.e. we can view the neurons weights as a prototype/template the neuron is looking for.

The relation to the cosine and many of the dot product's properties become clear geometrically

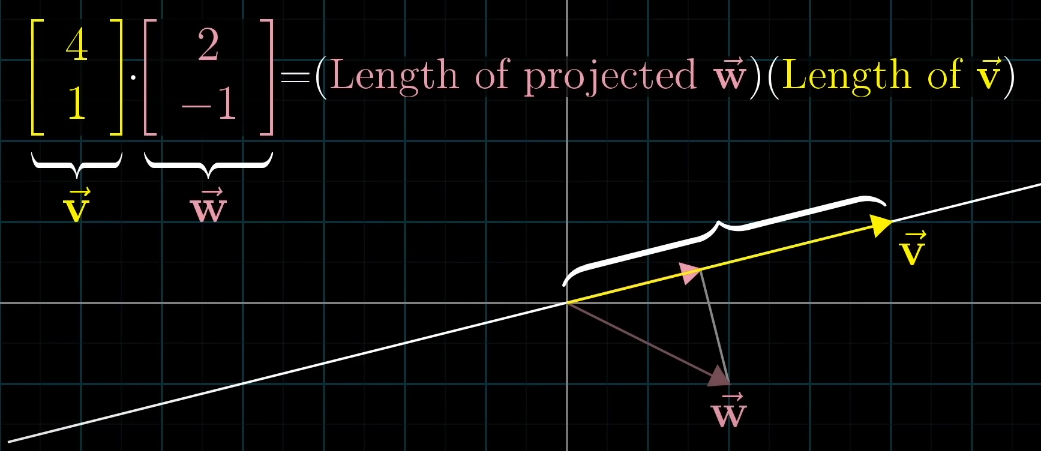
Project one vector onto another and multiply the length of the other with the resulting vector.
The head of the projected vector follows from drawing an orthogonal line from the head of one vector to another.
→ For two vectors on the unit circle, this projection is the cosine of the angle between them.
→ Order does not matter.

Dot product is positive if they point into the same direction, negative for opposing directions:

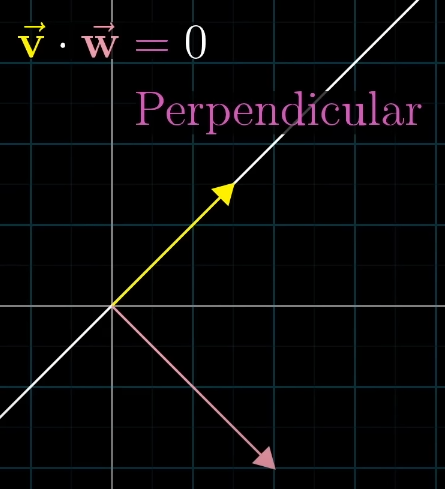
The projected vector $\vec{w}$ has length $0$ if the vectors are perpendicular:

Indifference of order:

Scaling one of those vectors by 2 → dot product is exactly 2x bigger:

$$(2\vec{v})\cdot \vec{w}=2(\vec{v}\cdot \vec{w})$$

---

Cauchy-Schwarz inequality

$\forall \mathbf{x},\mathbf{y}\in {\mathbb{C}}^n$

$$|⟨\mathbf{x},\mathbf{y}⟩|\le \Vert \mathbf{x}{\Vert }_2\cdot \Vert \mathbf{y}{\Vert }_2$$

Furthermore, $|⟨\mathbf{x},\mathbf{y}⟩|=\Vert \mathbf{x}{\Vert }_2\cdot \Vert \mathbf{y}{\Vert }_2⟺\exists \alpha \in \mathbb{C}:\mathbf{x}=\alpha \mathbf{y}$
This inequality is special to the euclidean norm and inner product spaces. It states that the absolute value of the inner product of two vectors is at most the product of their norms, with equality if and only if the vectors are linearly dependent.
Proof: $|\cos (\theta )|\le 1⟹|{\mathbf{a}}^T\mathbf{b}|=\Vert \mathbf{a}\Vert \cdot \Vert \mathbf{b}\Vert \cos (\theta )\le \Vert \mathbf{a}\Vert \cdot \Vert \mathbf{b}\Vert$

Link to original

The equation $⟨a,b⟩=⟨a,c⟩$ has three possible solutions.

i) $a=0$
ii) $b=c$
iii) $a\perp (b-c)$, i.e. $⟨a,b-c⟩=0$

So if two vectors have the same dot product with a third vector, they either are the same vector, or the third vector is orthogonal to their difference (spanning a hyperplane between them).

---

Dot product is a type of inner product

---

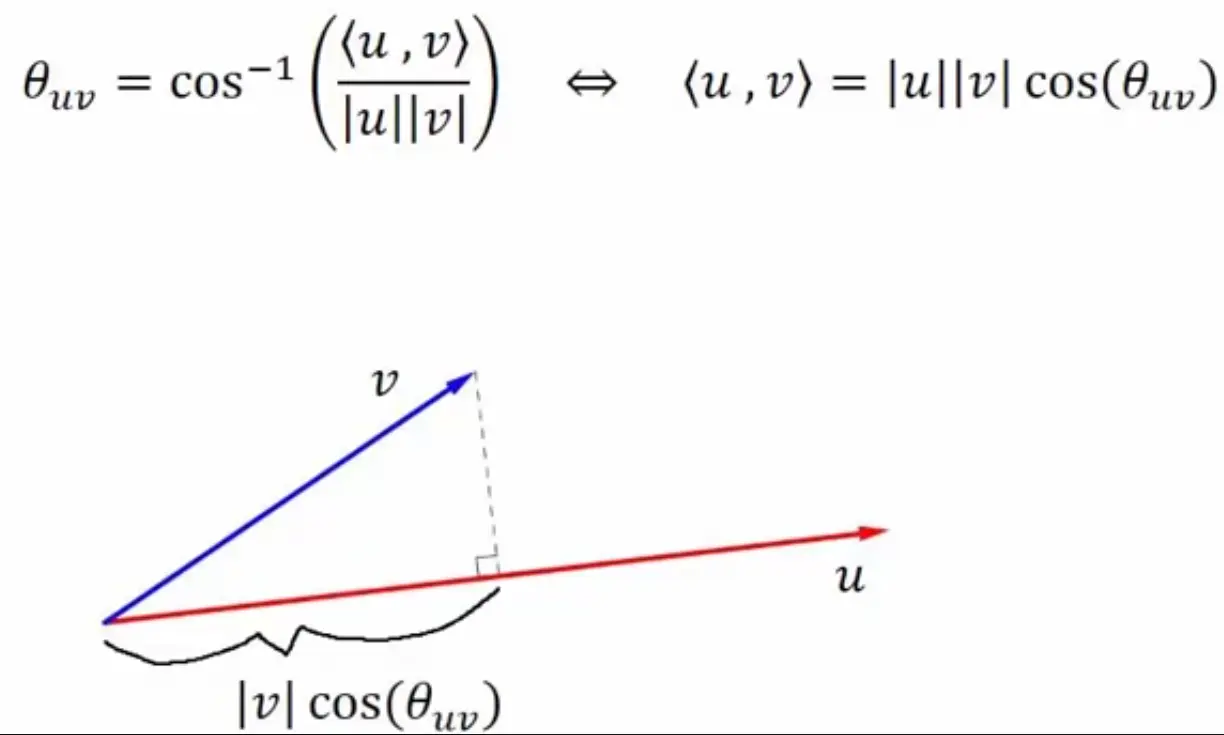
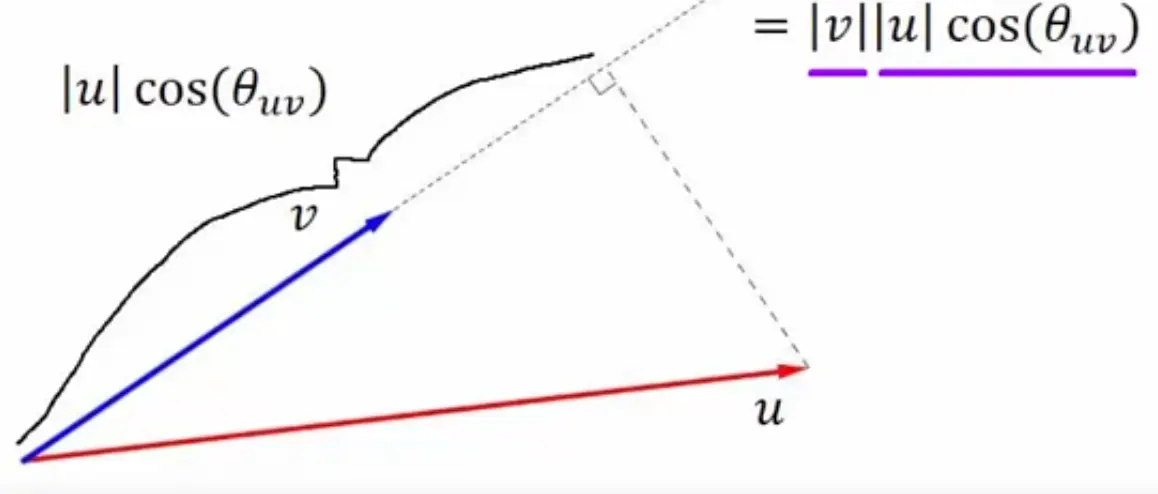
Intuition for the cosine formula
khan ac yt

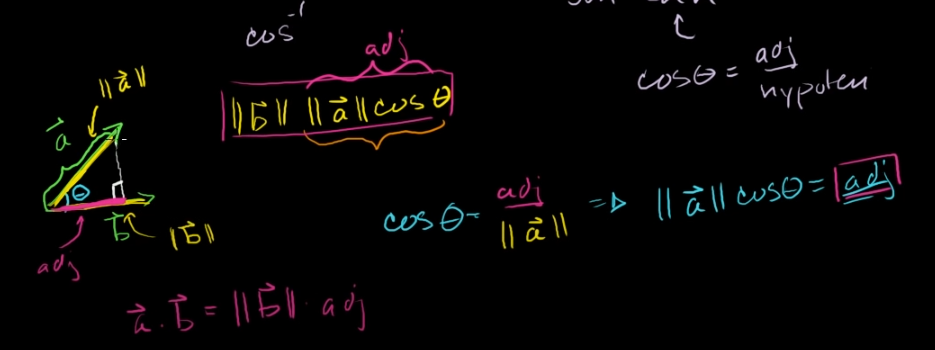
Multiplying the length of $\vec{b}$ times the amount of $\vec{a}$ thats going in the same direction as $\vec{b}$

If they are perfectly parallel, the dot-product is simply $||\vec{a}||||\vec{b}||\cos (90)$, so simply their lengths multiplied!

TODO go through this rq on paper

https://youtu.be/tdwFdzVqito (cosine formula, dot vs cross) 3b1b

See also Matrix Vector Product Intuition