function

Function

Let $A,B\ne \varnothing$
A (typed) function from $A$ to $B$ is the triple $(A,B,R_f)$, where $A$ is the domain, $B$ is the codomain, and $R_f$ is a relation also called the graph of the function with the following property:
$R_f\subseteq A\times B:\forall x\in A\exists !y\in B:x{R}_{f}y$ (each element of $A$ is related to exactly one (=unique) element of $B$).
Notation:
Instead of $(A,B,R_f)$, we write $f:A\to B$ ($f$ maps set $A$ to set $B$)
Instead of $x{R}_{f}y$, we write $f(x)=y$ or $x\mapsto f(x)$ (point $x$ is mapped to point $f(x)$)

Function graph

The graph of a function $f$ is the set of ordered pairs $(x,y)$, with the relation $f(x)=y$

$$R_f=\{x,f(x)\mid x\in A\}$$

Link to original

Domain of a function

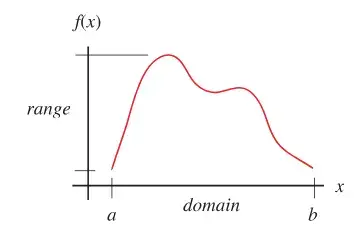
If $f:A\to B$ is a function from set $A$ to set $B$, then the domain of $f$ is the set $A$.

Link to original

Codomain

For a function $f:A\to B$, the set $B$ is called the codomain of $f$.
It is the (declared) set within which all outputs of $f$ must lie, but not all elements of $B$ need to be actual outputs of $f$.

Link to original

Image / Range

The image of a function $f:A\to B$ is the set of all output values it can produce:

$$\text{Im}(f):=\{f(a)\mid a\in A\}\subseteq B$$

It is a subset of the codomain $B$. Iff $f$ is surjective, then $\text{Im}(f)=B$.
Usually, the image of $A$ under $f$ is called the range of $f$, whereas $\{f(s)|s\in S\}\subseteq B$ is called the image of $S\subseteq A$ under $f$.

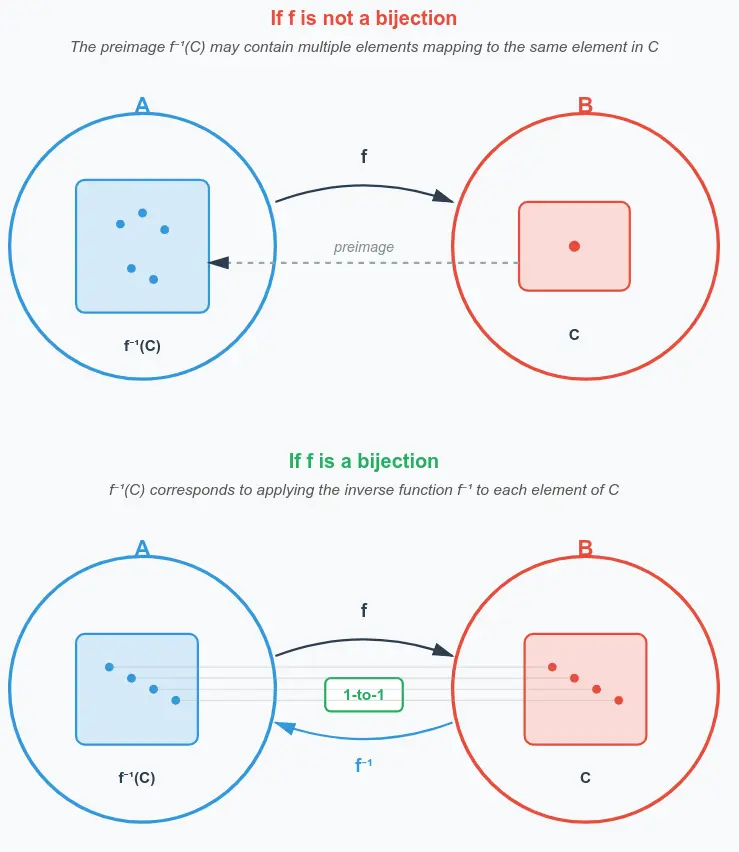
Link to original

Preimage / inverse image

For a function $f:A\to B$ and a subset $C\subseteq B$, the preimage or inverse image of $C$ under $f$ is defined as:

$$f^{-1}(C):=\{x\in A:f(x)\in C\}$$

is the set of all elements in the domain $A$ that get mapped to elements in $C$ under $f$.
Note that this notation does not require $f$ to be invertible – that would be $f(\cdot {)}^{-1}$ – it just describes which inputs lead to outputs in $C$.

Visuals $f$ is not a bijection, the preimage $f^{-1}(C)$ may contain multiple elements that all map to the same element in $C$. Iff $f$ is a bijection, then $f^{-1}(C)$ corresponds to applying the inverse function $f^{-1}$ to each element of $C$. code

If

Link to original

Function transformations

$f(x+c)$ shifts your function to the left, as it reaches the same output $c$ units earlier.
$f(x)+c$ shifts your function up by $c$ units.
$f(cx)$ compresses your function horizontally by a factor of $c$ (if $c>1$) or stretches it (if $0<c<1$).
$cf(x)$ stretches your function vertically by a factor of $c$ (if $c>1$) or compresses it (if $0<c<1$).
$-f(x)$ reflects your function at the x-axis.

EXAMPLE

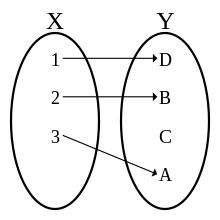
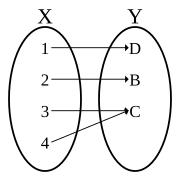
Injective (one-to-one) function

A function $f:A\to B$ is called injective if $\forall x_1,x_2\in A:f(x_1)=f(x_2)⟹x_1=x_2$
Or conversely: $\forall x_1,x_2\in A:x_1\ne x_2⟹f(x_1)\ne f(x_2)$

(an injective but not surjective function)

Link to original

Surjective (onto) function

A function $f:A\to B$ is called surjective if $\forall y\in B\exists x\in A:f(x)=y$
In words: every element in the codomain is the image of at least one element in the domain.

(a surjective not injective function)

Link to original

Bijective function

A function $f:A\to B$ is called bijective if it is both injective and surjective.
A bijection basically means that there is a one-to-one correspondence between all elements of the domain and the codomain: For every unique element in $A$, there is a unique element in $B$.

Link to original

EXAMPLE

$f_1:\mathbb{R}\to {\mathbb{R}}_0^{+}:x\mapsto x^2$ is not injective, because $f_1(-1)=f_1(1)$ and it is not surjective, because $f_1(x)\ge 0\forall x\in \mathbb{R}$ (negative real numbers are not in the codomain).
$f_2:{\mathbb{R}}_0^{+}\to \mathbb{R},x\mapsto x^2$ is injective, but not surjective because we canot reach negative numbers.
$f_3:\mathbb{R}\to {\mathbb{R}}_0^{+},x\mapsto x^2$ is not injective but surjective ($x^2=z$ has a solution for all $z\in {\mathbb{R}}_0^{+}$).
$f_4:{\mathbb{R}}_0^{+}\to {\mathbb{R}}_0^{+},x\mapsto x^2$ is bijective.

---

$f_1:\mathbb{N}\to \mathbb{N}:n\mapsto n+1$ is a bijection
$f_2:n\to \mathbb{N}:n\mapsto n-1$ is not a function, since $f(0)$ is not defined.
$g_1:\mathbb{Z}\to \mathbb{Z}:n\mapsto -n$ is a bijection
$g_2:\mathbb{Z}\to \mathbb{Z}:n\mapsto 1-n$ is a bijection
$h_1:{\mathbb{R}}^2\to {\mathbb{R}}^2:(x,y)\mapsto (y,-x)$ is a bijection (it’s a 90 degree rotation). Also, $x_1=x_2⟹y_1\ne y_2$ and vice versa.

$h_2:{\mathbb{R}}^2\to {\mathbb{R}}^2:(x,y)\mapsto (x-y,x+y)$ (hint: set up systems of equations) Injectivity: Assuming equal outputs for equal inputs:

\begin{align*}
(x_{1}, y_{1}), (x_{2}, y_{2}) \in \mathbb{R}^{2}: & h_{2}(x_{1}, y_{1}) = h_{2}(x_{2}, y_{2}) \
& \iff (x_{1} - y_{1}, x_{1} + y_{1}) = (x_{2} - y_{2}, x_{2} + y_{2}) \
& \iff \begin{cases}
x_{1} - y_{1} = x_{2} - y_{2} \
x_{1} + y_{1} = x_{2} + y_{2}
\end{cases} \
& \iff \begin{cases}
x_{1} = x_{2} \
y_{1} = y_{2}
\end{cases} \
& \iff (x_{1}, y_{1}) = (x_{2}, y_{2})
\end{align*}

Surjectivity: For every $(a,b)\in {\mathbb{R}}^2$, we can find a $(x,y)\in {\mathbb{R}}^2$ such that $h_2(x,y)=(a,b)$:

\begin{align*}
(a,b) \in \mathbb{R}^{2}: & h_{2}(x,y) = (a,b) \
& \iff (x-y, x+y) = (a,b) \
& \iff \begin{cases}
x - y = a \
x + y = b
\end{cases} \
& \iff \begin{cases}
x = \frac{a+b}{2} \
y = \frac{b-a}{2}
\end{cases} \
& \iff (x,y) = \left( \frac{a+b}{2}, \frac{b-a}{2} \right)
\end{align*}

→ $h_{2}$ is bijective.

If a function from two finite sets of equal length is injective, it is also surjective (→ bijective).

Let $A,B$ be finite sets, $|A|=|B|=n$, $A=\{a_1,\dots ,a_n\}$.
$f:A\to B,f(a_i)=b_i⟹f\text{ injective}⟺f\text{ surjective}$

Proof:
Injective $⟹$ surjective:
$b_1,\dots b_n$ are pairwise different: $b_i=b_j⟹a_i=a_j⟹i=j$ (injective)
$⟹\underset{=f(A)=\{f(x)\mid x\in A\}}{\underbrace{\{b_1,\dots ,b_n\}}}=B$
(“slight abuse of notation” … in logic, they use $f[B]$ for the image of $B$ under $f$)]
$f(A)=B$ → surjective
Surjective $⟹$ injective:
Assumption $f(A)=B$
Assume it’s not injective $\exists k\ne l:a_k\ne a_l\wedge \underset{f(a_k)}{\underbrace{b_k}}=\underset{f(a_l)}{\underbrace{b_k}}$
$⟹|\underset{f(A)}{\underbrace{\{f(a_1),f(a_2),\dots f(a_n)\}}}|<n⟹f(A)\ne B⟹$ not surjective.
Strictly formally, we would need to first define the cardinality with bijective functions to get to the definition of equality for bijective images…
But uhm this thing makes quite obviously sense if you just look at the definition.

The theorem above can be extended to inifinite sets: Two infinite sets have the same size if there is a bijection between them.

→ Not all infinite sets are the same size! (since we cannot find a bijection between them)

Transclude of composition

Identity function

The identity function on a set $A$ is the function ${\text{id}}_A:A\to A,x\mapsto x$.

Transclude of inverse-function

Function evaluation

$B^A$ denotes the set of all functions $A\to B$ (hom-class or exponential object).

$$\text{ev}:B^A\times A\to B,f\mapsto f(x)$$

Read: The evaluation applies a function $f:A\to B$ to an argument $x\in A$ and returns the result $f(x)\in B$.

---

Every time there are multiple pathways / ways of implementing something, there’s a function.

---

A note on notation

If I don’t specify for which sets a function is defined, it’s usually complex-valued unless it’s obvious from context that it’s something else.